2016第七屆藍橋杯大賽C組省賽
第一題
報紙頁數
X星球日報和我們地球的城市早報是一樣的,
都是一些單獨的紙張疊在一起而已。每張紙印有4版。
比如,某張報紙包含的4頁是:5,6,11,12,
可以確定它應該是最上邊的第2張報紙。
我們在太空中撿到了一張X星球的報紙,4個頁碼分別是:
1125,1126,1727,1728
請你計算這份報紙一共多少頁(也就是最大頁碼,並不是用了幾張紙哦)?
請填寫表示總頁數的數字。
注意:你提交的應該是一個整數,不要填寫任何多餘的內容或說明性文字。
答案:
題目還是沒看懂第二題
煤球數目
有一堆煤球,堆成三角稜錐形。具體:
第一層放1個,
第二層3個(排列成三角形),
第三層6個(排列成三角形),
第四層10個(排列成三角形),
….
如果一共有100層,共有多少個煤球?
請填表示煤球總數目的數字。
//題目不難,用一個函式計算第幾層有多少個,然後加到總和
/*for(int i=1; i<=100; i++) {
sum += fun(i);
}*/
//100層煤球一共有多少個
//100層煤球一共有多少個
//100層煤球一共有多少個
//不要再粗心寫5050了,勿忘勿忘勿忘
#include<stdio.h>
int fun(int n) {
int sum = 0;
for(int i=1; i<=n; i++) {
sum += i;
}
return sum;
}
int main() {
int //另一種解法
#include <stdio.h>
int main()
{
int i,n,sum;
sum = 0;
n = 0;
for (i = 1; i <= 100; ++i)
{
//
n +=i;
sum += n;
printf("%d\n" 第三題
平方怪圈
如果把一個正整數的每一位都平方後再求和,得到一個新的正整數。
對新產生的正整數再做同樣的處理。
如此一來,你會發現,不管開始取的是什麼數字,
最終如果不是落入1,就是落入同一個迴圈圈。
請寫出這個迴圈圈中最大的那個數字。
請填寫該最大數字。
#include<iostream>
#include<cstring>
using namespace std;
char s[100];
int fun(char *s) {
int sum = 0;
int len = strlen(s);
//每個數都平方
for(int i=0; i<len; i++) {
sum += (s[i]-'0')*(s[i]-'0');
}
return sum;
}
int main() {
int num = 14;
int MAX = 0;
//根據題意,設定迴圈50次
for(int i=0; i<50; i++) {
//因為要檢測一個數一共有幾位,所以把他轉化為字串,利用strlen就可以檢測到,然後每個數都平方,再返回一個數值
sprintf(s, "%d", num);
num = fun(s);
//每一次都比較,把最大的放出來
MAX = max(MAX, num);
}
cout << MAX << endl;
return 0;
}第四題
列印方格
小明想在控制檯上輸出 m x n 個方格。
比如 10x4的,輸出的樣子是:
以下是小明寫的程式,請你分析其流程,填寫劃線部分缺少的程式碼
#include<stdio.h>
void f(int m, int n) {
int row;
int col;
for(row=0; row<n; row++) {
for(col=0; col<m; col++) printf("+---");
printf("+\n");
for(col=0; col<m; col++) printf("| ");
printf("\n");
}
printf("+");
//填寫程式碼
printf("\n");
}
int main() {
f(10,4);
return 0;
}//通過簡單的除錯,可以看出來。不難,題目很水,別粗心就好了
#include<stdio.h>
void f(int m, int n) {
int row;
int col;
for(row=0; row<n; row++) {
for(col=0; col<m; col++) printf("+---");
printf("+\n");
for(col=0; col<m; col++) printf("| ");
printf("|\n");
}
printf("+");
//迴圈列印----------------------------------------
for(col=0; col<m; col++) printf("---+");
printf("\n");
}
int main() {
f(10,4);
return 0;
}第五題
快速排序
排序在各種場合經常被用到。
快速排序是十分常用的高效率的演算法。
其思想是:先選一個“標尺”,
用它把整個佇列過一遍篩子,
以保證:其左邊的元素都不大於它,其右邊的元素都不小於它。
這樣,排序問題就被分割為兩個子區間。
再分別對子區間排序就可以了。
下面的程式碼是一種實現,請分析並填寫劃線部分缺少的程式碼。
複製程式碼
#include <stdio.h>
void swap(int a[], int i, int j)
{
int t = a[i];
a[i] = a[j];
a[j] = t;
}
int partition(int a[], int p, int r)
{
int i = p;
int j = r + 1;
int x = a[p];
while(1){
while(i<r && a[++i]<x);
while(a[--j]>x);
if(i>=j) break;
swap(a,i,j);
}
______________________;
return j;
}
void quicksort(int a[], int p, int r)
{
if(p<r){
int q = partition(a,p,r);
quicksort(a,p,q-1);
quicksort(a,q+1,r);
}
}
int main()
{
int i;
int a[] = {5,13,6,24,2,8,19,27,6,12,1,17};
int N = 12;
quicksort(a, 0, N-1);
for(i=0; i<N; i++) printf("%d ", a[i]);
printf("\n");
return 0;
}答案:看不懂的,建議百度快排,看一下原理
swap(a,p,j)
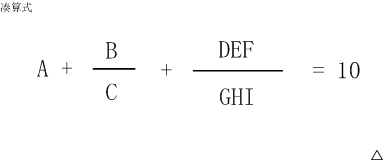
湊算式
這個算式中A~I代表1~9的數字,不同的字母代表不同的數字。
比如:
6+8/3+952/714 就是一種解法,
5+3/1+972/486 是另一種解法。
這個算式一共有多少種解法?
注意:你提交應該是個整數,不要填寫任何多餘的內容或說明性文字。
//double型,這種題還是for好用啊!!!!!!
#include<stdio.h>
int main() {
double a, b, c, d, e, f, g, h, i;
double t1, t2, t3;
int sum = 0;
for(a=1; a<=9; a++) {
for(b=1; b<=9; b++) {
for(c=1; c<=9; c++) {
for(d=1; d<=9; d++) {
for(e=1; e<=9; e++) {
for(f=1; f<=9; f++) {
for(g=1; g<=9; g++) {
for(h=1; h<=9; h++) {
for(i=1; i<=9; i++) {
if(a!=b && a!=c && a!=d && a!=e && a!=f && a!=g && a!=h && a!=i) {
if(b!=c && b!=d && b!=e && b!=g && b!=h && b!=i && b!=f) {
if(c!=d && c!=e && c!=f && c!=g && c!=h && c!=i) {
if(d!=e && d!=f && d!=g && d!=h && d!=i) {
if(e!=f && e!=g && e!=h && e!=i) {
if(f!=g && f!=h && f!=i) {
if(g!=h && g!=i) {
if(h!=i) {
t1 = a;
t2 = b/c;
t3 = (d*100+e*10+f)/(g*100+h*10+i);
if(t1+t2+t3==10) {
sum++;
printf("%f %f %f %f %f %f %f %f %f\n", a, b, c, d, e, f, g, h, i);
printf("%d\n", sum);
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
}
} //另一種使用DFS的方法
//我有博文專門介紹DFS的,大家可以去看一下
//這裡主要是判斷結束的條件有點難度
#include<stdio.h>
//a b c d e f g h i
int a[10];
bool isVisit[10];
int t1, t2, t3, sum=0;
void dfs(int num)
{
if (num == 10)
{
//讓後面兩個分數通分
t1 = a[3] * (a[7] * 100 + a[8] * 10 + a[9]);
t2 = a[2] * (a[7] * 100 + a[8] * 10 + a[9]);
t3 = a[3] * (a[4] * 100 + a[5] * 10 + a[6]);
//如果後面兩個式子是整數,則滿足條件,具體為什麼,自己好好想一下
//一個整數肯定是加一個整數才能等於一個整數
if((t2+t3) % t1 == 0){
if(a[1] + ((t2 + t3) / t1) == 10) {
sum++;
}
}
}
for (int i = 1; i < 10; i++)
{
if (isVisit[i] == 0)
{
isVisit[i] = 1;
a[num] = i;
dfs(num + 1);
isVisit[i] = 0;
}
}
}
int main()
{
dfs(1);
printf("%d\n", sum);
return 0;
} 第六題
寒假作業
現在小學的數學題目也不是那麼好玩的。
看看這個寒假作業:
□ + □ = □
□ - □ = □
□ × □ = □
□ ÷ □ = □
(如果顯示不出來,可以參見【圖1.jpg】)
每個方塊代表1~13中的某一個數字,但不能重複。
比如:
6 + 7 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
以及:
7 + 6 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
就算兩種解法。(加法,乘法交換律後算不同的方案)
你一共找到了多少種方案?
請填寫表示方案數目的整數。
注意:你提交的應該是一個整數,不要填寫任何多餘的內容或說明性文字。
//當時第一時間就想到這種辦法,但這樣要執行很久很久才可以得出答案, 遍歷所有可能,但step==13的時候判斷條件,滿足則SUM++;
#include<stdio.h>
int book[14], a[14];
int sum = 0;
void dfs(int step) {
if(step == 13) {
if(a[1]+a[2]==a[3] && a[4]-a[5]==a[6] && a[7]*a[8]==a[9] && a[10]/a[11]==a[12]) {
sum++;
}
}
for(int i=1; i<=13; i++) {
if(book[i] == 0) {
book[i] = 1;
a[step] = i;
dfs(step+1);
book[i] = 0;
}
}
}
int main() {
dfs(1);
printf("%d", sum);
return 0;
} //每迴圈完一個式子,就判斷是否滿足條件,如果不滿足就跳過,這樣可以很快速出答案
#include<stdio.h>
int book[14], a[14];
int sum = 0;
int judge(int n) {
if(n == 3) {
if(a[1] + a[2] != a[3])
return 0;
}
if(n == 6) {
if(a[4] - a[5] != a[6])
return 0;
}
if(n == 9) {
if(a[7] * a[8] != a[9])
return 0;
}
if(n == 12) {
if(a[10]%a[11]!=0 || a[10]/a[11]!=a[12])
return 0;
sum++;
printf("%d + %d = %d\n", a[1],a[2],a[3]);
printf("%d - %d = %d\n", a[4],a[5],a[6]);
printf("%d * %d = %d\n", a[7],a[8],a[9]);
printf("%d / %d = %d\n", a[10],a[11],a[12]);
printf("\n\n\n");
}
return 1;
}
void dfs(int step) {
for(int i=1; i<=13; i++) {
if(book[i] == 0) {
book[i] = 1;
a[step] = i;
if(judge(step) == 0) {
book[i] = 0;
continue;
}
dfs(step+1);
book[i] = 0;
}
}
}
int main() {
dfs(1);
printf("%d", sum);
return 0;
} 第八題
冰雹數
任意給定一個正整數N,
如果是偶數,執行: N / 2
如果是奇數,執行: N * 3 + 1
生成的新的數字再執行同樣的動作,迴圈往復。
通過觀察發現,這個數字會一會兒上升到很高,
一會兒又降落下來。
就這樣起起落落的,但最終必會落到“1”
這有點像小冰雹粒子在冰雹雲中翻滾增長的樣子。
比如N=9
9,28,14,7,22,11,34,17,52,26,13,40,20,10,5,16,8,4,2,1
可以看到,N=9的時候,這個“小冰雹”最高衝到了52這個高度。
輸入格式:
一個正整數N(N<1000000)
輸出格式:
一個正整數,表示不大於N的數字,經過冰雹數變換過程中,最高衝到了多少。
例如,輸入:
10
程式應該輸出:
52
再例如,輸入:
100
程式應該輸出:
9232
//這道題反正我無語
//一個正整數,表示不大於N的數字,經過冰雹數變換過程中,最高衝到了多少。
//表示不大於N的數字,經過冰雹數變換過程中,最高衝到了多少。
//不大於N的數字,最高衝到了多少。
//我的北京啊,無緣啊
#include<stdio.h>
int n, MAX=0;
void fun(int n) {
if(n > MAX) MAX = n;
if(n == 1) return;
if(n % 2 == 0) {
n /= 2;
} else {
n = n * 3 + 1;
}
fun(n);
}
int main() {
for(int i=9; i<=100; i++) {
printf("%d ", i);
fun(i);
printf("%d\n", MAX);
MAX = 0;
}
return 0;
}卡片換位
你玩過華容道的遊戲嗎?
這是個類似的,但更簡單的遊戲。
看下面 3 x 2 的格子
+—+—+—+
| A | * | * |
+—+—+—+
| B | | * |
+—+—+—+
在其中放5張牌,其中A代表關羽,B代表張飛,* 代表士兵。
還有一個格子是空著的。
你可以把一張牌移動到相鄰的空格中去(對角不算相鄰)。
遊戲的目標是:關羽和張飛交換位置,其它的牌隨便在哪裡都可以。
輸入格式:
輸入兩行6個字元表示當前的局面
輸出格式:
一個整數,表示最少多少步,才能把AB換位(其它牌位置隨意)
例如,輸入:
* A
**B
程式應該輸出:
17
再例如,輸入:
A B
程式應該輸出:
12
暫時不會,留坑密碼脫落
X星球的考古學家發現了一批古代留下來的密碼。
這些密碼是由A、B、C、D 四種植物的種子串成的序列。
仔細分析發現,這些密碼串當初應該是前後對稱的(也就是我們說的映象串)。
由於年代久遠,其中許多種子脫落了,因而可能會失去映象的特徵。
你的任務是:
給定一個現在看到的密碼串,計算一下從當初的狀態,它要至少脫落多少個種子,才可能會變成現在的樣子。
輸入一行,表示現在看到的密碼串(長度不大於1000)
要求輸出一個正整數,表示至少脫落了多少個種子。
例如,輸入:
ABCBA
則程式應該輸出:
0
再例如,輸入:
ABDCDCBABC
則程式應該輸出:
3
暫時不會,留坑