我們有兩個正態分佈：N(2,4)和N(3,5)，現在想求出靠近兩者均值的等概率點，如圖所示：

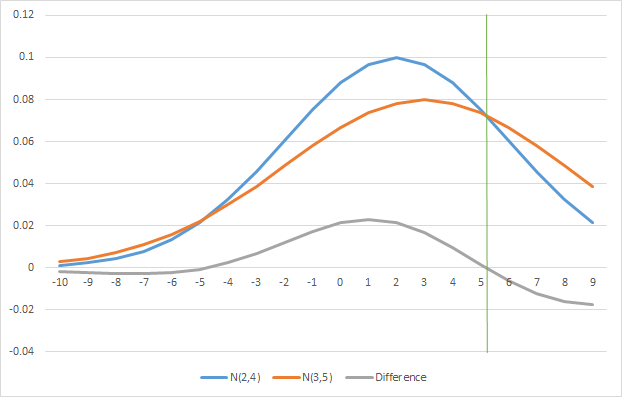
其中Difference=N(2,4)-N(3,5)，即為我們下列程式碼中的函式f

#! /usr/bin/python3
#-*-coding:utf-8-*-

from scipy.optimize import fsolve
import numpy as np
import math

#定義函式（方程f(x|arg)=0）
def f(x,*arg): #len(arg)=4, arg=(miu_1,miu_2,sigma_1,sigma_2)
    f1=math.exp(-(x-arg[0
 
])**2/2/arg[2]**2)/arg[2]/math.sqrt(2*math.pi)
    f2=math.exp(-(x-arg[1])**2/2/arg[3]**2)/arg[3]/math.sqrt(2*math.pi)
    return(f1-f2)


x0=(2.5,2,3,4,5)
result=fsolve(f,x0=x0[0],args=x0[1:])
print(result)
#輸出：[ 5.19949597]

可以看到解出的根和我們圖上的標註的位置非常接近，也就是說這個根是我們所需要的的解。
注意在fsolve函式裡，得註明前多少個f的引數是我們方程中要求解的變數(x0的長度)，哪些是方程中的引數(args)
對於具有多個根的方程，x0的具體數值很重要，因為初解很大程度上決定了根收斂的方向。
為了求得靠近兩分佈中心位置的根，初解最好選為兩均值的均值，在這裡我們將x0設為(2+3)/2=2.5
如果設為1，可以看到Difference在1處的導數幾乎為0，因而根會收斂得非常奇葩，實際操作做了一下，輸出的結果為[-152.18013068]，遠遠偏離分佈中心位置。因為fsolve有一個預設引數xtol=1.49012e-08，只要當兩次迭代結果之間的差值小於xtol就會終止迭代，所以不難理解為什麼方程只有兩個不大的根，卻得出了一個這麼奇怪的結果。
如果將x0設為0，就可以得到另一個根：[-4.75505152]，這個是較為遠離分佈中心的根。

因為在這裡我們只求解一個變數x，所以在定義函式的時候，只需返回一個值（一個約束），如果是求解多元方程，則在定義函式的時候返回一個list即可，fsolve會自動求使得list的所有元素均為0的根