樸素貝葉斯分類器訓練過程分析
阿新 • • 發佈:2019-02-10
轉載來源,系列閱讀:http://pocore.com/blog/article_495.html
這是一個識別論壇不當言論的案例
步驟一:獲得這個問題的全部特徵(標稱型)
所謂標稱型資料:是可以化成0 1表示的資料
用於案例訓練的資料如下:
dataSet: [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'], ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'], ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'], ['stop', 'posting', 'stupid', 'worthless', 'garbage'], ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'], ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
獲得這個問題的全部特徵做法如下
依次迴圈取得一行
document: ['my', 'dog', 'has', 'flea', 'problems', 'help', 'please']
set化可獲取詞列表{'please', 'has', 'flea', 'help', 'my', 'problems', 'dog'}
迴圈每步和上一步獲得set取並集
{'please', 'maybe', 'not', 'him', 'to', 'has', 'stupid', 'flea', 'help', 'my', 'problems', 'take', 'park', 'dog'}
...
list化最終得到訓練資料的不重複詞庫如下:
word:['love', 'please', 'not', 'has', 'how', 'stop', 'is', 'cute', 'dog', 'ate', 'worthless', 'I', 'stupid', 'flea', 'dalmation', 'problems', 'take', 'park', 'buying', 'to', 'steak', 'food', 'posting', 'quit', 'so', 'maybe', 'licks', 'him', 'mr', 'my', 'help', 'garbage']
步驟二:實現輸入詞條得到上一步的詞庫狀態特徵表示列表
上一步得到的不重複詞庫:
vocabList: ['has', 'stop', 'him', 'not', 'take', 'how', 'to', 'dalmation', 'maybe', 'is', 'food', 'steak', 'dog', 'my', 'I', 'stupid', 'posting', 'licks', 'park', 'please', 'worthless', 'problems', 'cute', 'garbage', 'ate', 'flea', 'mr', 'help', 'love', 'quit', 'buying', 'so']
舉例要獲取詞庫特徵表示列表的輸入語句列表表示如下
inputSet: ['dog','stop']
我們初始化一個和詞庫等長的表示列表
returnVec: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
依次判斷inputSet中的單詞是否在vocabList中,如果在則獲得其在vocabList中的序號位置index並置returnVec
對應位置的置為1
如果發現某些單詞不存在於詞庫中,則忽略即可
按照上面步驟通過上面的inputSet得到的表示列表為
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
下面結合理論進行下步處理
貝葉斯準則公式:
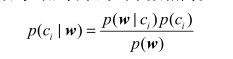
其中w是一組特徵值
根據本應用場景解釋,公式左邊表示在語句單詞出現列表為w情況下被劃分到類別c的概率。
右邊上面和左邊剛好相反的部分公式解釋是:被劃分到類別c的情況下語句單詞出現列表為w的概率
p(ci)為訓練資料中被劃分到類別ci的概率
p(w)為訓練資料中出現列表為w的概率
可以簡單理解貝葉斯準則做了這樣一件事:巧妙的提出了一種在已知P(A|B)可求的情況下求出P(B|A)的方法
這裡有一個理論上不成立但實際使用效果很好的假設:各個單詞出現在不同分類的事件相互獨立,其實一般是有關係的,但是應用這個假設能簡化計算過程,接下來的計算會用到這個假設
根據這個假設我們可以得到p(w|c)=p(w1|c)p(w2|c)....
其中w={w1,w2...}
步驟三:樸素貝葉斯分類訓練過程
1.將訓練資料轉化為特徵值列表表示

2.輸入條件
(1.)trainMatrix
(2.)trainCategory: [0, 1, 0, 1, 0, 1] 是否是不當言論
3.開始訓練(訓練目的,今後給出新的文件判斷是否不當言論)
上面的資料我們可以計算得到以下資料
文件數目:6
numWords:32 每個文件特徵數
利用trainCategory 計算可得 P(是不當言論概率) pAbusive=0.5 對應上面貝葉斯準則的p(c=1)
初始化兩個如下的numWords個值為0的陣列用於狀態暫存
p0Num,p1Num

p0Denom,p1Denom = 0.0
遍歷訓練文件
演算法過程舉例:
如文件0類別為0
p0Num加上trainMatrix[0]變為
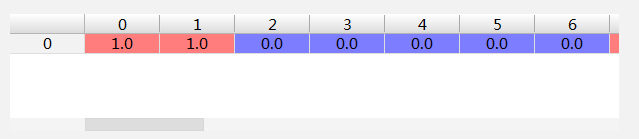
p0Denom加上trainMatrix[0]詞彙數變為7.0
...
如文件1類別為1
p1Num加上trainMatrix[1]
p1Denom加上trainMatrix[1]詞彙數變為8.0
迴圈最終得到
p0Num記錄類別為0時各個特徵的次數陣列
p0Denom記錄類別為0時所有為0文件單詞總數:24.0
p1Num記錄類別為1時各個特徵的次數陣列
p1Denom記錄類別為1時所有為1文件單詞總數:19.0
通過公式
p1Vec = p1Num / p1Denom
對應上面的貝葉斯準則可以得到p(w1|c=1) p(w2|c=1).....

同樣通過公式
p0Vec = p0Num / p0Denom
對應上面的貝葉斯準則可以得到p(w1|c=0) p(w2|c=0).....
至此我們需要的幾個關鍵概率都已經計算出來了
改進:
1. p(w 0 |1)p(w 1 |1)p(w 2 |1) 。如果其中一個概率值為0,那麼最後的乘積也為0。為降低這種影響,可以將所有詞的出現數初始化為1,並將分母初始化為2
2.當計算乘積p(w 0 |c i )p(w 1 |c i )p(w 2 |c i )...p(w N |c i ) 時,由於大部分因子都非常小,所以程式會下溢位或者得到不正確的答案通過求對數可以避免下溢位或者浮點數舍入導致的錯誤
利用分類器進行真實分類
輸入:listOPosts,listClasses 第一個儲存文件,第二個儲存文件標記類別
testEntry=['love','my','dalmation'] 要測試分類的句子片語
根據listOPosts,listClasses計算得到
p0V,用於計算p(w|(c=0))
p1V,用於計算p(w|(c=1))
pAb,p(c=1)概率
利用listOPosts 生成testEntry的詞向量陣列表示
thisDoc=[...]
利用thisDoc,p0V,p1V,pAb計算testEntry屬於的類別
因為我們只需要比較p(c=1|w)和p(c=0|w)的大小 而p(w)是固定的,所以上面的公式取對數之後只需要計算
p1=sum(thisDoc*p1V)+np.log(pAb)
p0=sum(thisDoc*p0V)+np.log(1.0-pAb)
因為其中thisDoc記錄了單詞是否出現,所以對應單個單詞出現就是p0V或者p1V概率,不出現自然就是0
比較上面的p0、p1大小即可知道最終分類
這個例子
p0=-7.694848072384611
p1=-9.826714493730215
因為p0>p1所以被歸類為0
演算法持續改進:
問題:如果一個詞在文件中出現不止一次,這可能意味著包含該詞是否出現在文件中所不能表達的某種資訊,這種方法被稱為詞袋模型
改進:
修改每次遇到單詞對應記錄不是置為1而是+1
