hdu-2142(擴充套件歐幾里得解不定方程)
阿新 • • 發佈:2019-02-10
Description
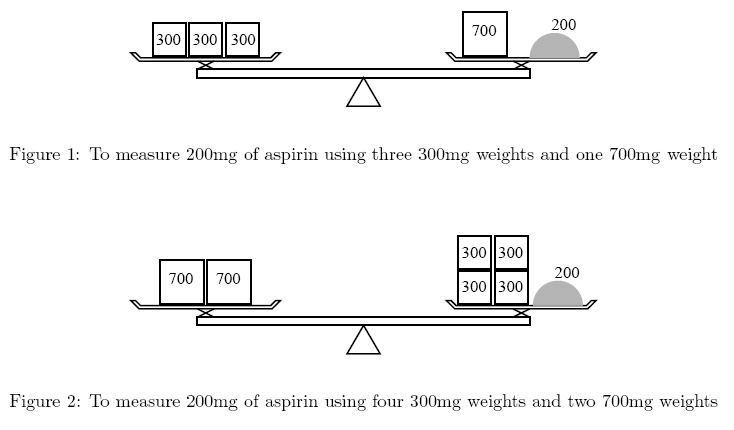
Ms. Iyo Kiffa-Australis has a balance and only two kinds of weights to measure a dose of medicine. For example, to measure 200mg of aspirin using 300mg weights and 700mg weights, she can put one 700mg weight on the side of the medicine and three 300mg weights on the opposite side (Figure 1). Although she could put four 300mg weights on the medicine side and two 700mg weights on the other (Figure 2), she would not choose this solution because it is less convenient to use more weights.You are asked to help her by calculating how many weights are required.
Input
The input is a sequence of datasets. A dataset is a line containing three positive integers a, b, and d separated by a space. The following relations hold: a != b, a <= 10000, b <= 10000, and d <= 50000. You may assume that it is possible to measure d mg using a combination of a mg and b mg weights. In other words, you need not consider "no solution" cases.The end of the input is indicated by a line containing three zeros separated by a space. It is not a dataset.
Output
- You can measure dmg using x many amg weights and y many bmg weights.
- The total number of weights (x + y) is the smallest among those pairs of nonnegative integers satisfying the previous condition.
- The total mass of weights (ax + by) is the smallest among those pairs of nonnegative integers satisfying the previous two conditions.
No extra characters (e.g. extra spaces) should appear in the output.
Sample Input
700 300 200 500 200 300 500 200 500 275 110 330 275 110 385 648 375 4002 3 1 10000 0 0 0
Sample Output
1 3 1 1 1 0 0 3 1 1 49 74 3333題目大意:給你倆個砝碼,重量a和重量b,讓你求得使用最少的砝碼數量且砝碼總重量也最小(即在|x|+|y|最小條件下,a*|x|+b*|y|也最小),稱出重物c.題目分析:很明顯我們可以列出方程a*x+b*y=c這個方程,但是怎麼求出滿足題意得x和y了。我們知道了通解x,y完全可以依靠列舉來找最小的,嘿嘿。暴力出奇跡,而且時間很快,遠遠少於5000m
 程式碼如下:
程式碼如下:#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
#define ll long long
using namespace std;
ll myabs(ll a)//abs()這個函式好像在poj上不支援long long 所以自己寫了一個
{
if (a<0) return -a;
else return a;
}
ll exgcd(ll a,ll b,ll &x,ll &y)
{
if (b==0) {
x=1;
y=0;
return a;
}
ll r=exgcd(b,a%b,x,y);
ll t=x;
x=y;
y=t-a/b*y;
return r;
}
void linear_equation(ll a,ll b,ll c,ll &x,ll &y)
{
ll d=exgcd(a,b,x,y);
if (c%d)
return ;
ll k=c/d;
x=x*k,y=y*k;
ll t1=b/d,x1;
ll t2=a/d,y1;
ll Min=myabs(x)+myabs(y);
ll ansx=x,ansy=y;
for (ll i=-100000;i<=100000;i++) {//列舉x與y,根據判斷條件來更新
x1=x+t1*i;
y1=y-t2*i;
if (myabs(x1)+myabs(y1)<Min||(myabs(x1)+myabs(y1)==Min&&(myabs(x1)*a+myabs(y1)*b<myabs(ansx)*a+myabs(ansy)*b))) {
ansx=x1;
ansy=y1;
Min=myabs(x1)+myabs(y1);
}
}
printf("%lld %lld\n",myabs(ansx),myabs(ansy));
}
int main()
{
ll a,b,d,x,y;
while (scanf("%lld%lld%lld",&a,&b,&d)!=EOF) {
if (a==0&&b==0&&d==0) break;
linear_equation(a,b,d,x,y);
}
return 0;
}
