在講歸併排序之前我們先來了解一下什麼是分治演算法。為什麼歸併排序屬於分治演算法的體現。

分治演算法

分治演算法基本思想就是將一個比較大規模的問題分解成為若干個規模較小的性質和原問題性質必須要保持一致。

分治演算法特徵

1.  該問題可以分解成為程式能夠執行的子問題。
2.  該問題能夠分解。意思就是問題具有最優子結構。
這裡我們可以理解成問題通過分解能夠遞迴的來實現解。
3.  該問題分解出來的子集問題得到的解能夠合併成為該問題的解。
這個非常重要，直接決定這個問題能否使用分治演算法，同時滿足這個條件意味著子集問題與原問題在結構上具有一致性。
4.  該問題分解出來的子集問題得出來的解是相互獨立的，意味著子集解中沒有交集。
這個直接影響分治演算法的效率，雖然我們也可以專門對交集做處理，但這樣會浪費大量時間。
 

歸併排序

是建立在歸併操作上的一種排序演算法，該方法基本思想採用了分治法來解決。
將已經有序的兩個序列集合合併來得到解，首先我們讓每個子集序列集有序化，再讓每個子集序列間段有序化然後合併得到解。

歸併演算法思路

1.申請三段空間，其中兩段空間用於儲存兩個序列集，另外一個儲存排序之後我們得到的結果，稱之為合併序列。
2.設定兩個指標，這兩個指標分別指向兩個待比較的序列子集的初始位置。
3.比較兩個指標所指向的元素值大小，將小的序列中的元素存入合併序列
中，然後移動合併序列和已經取出的元素的序列指標指向下一位。
4.重複步驟三做比較，直到一個序列的指標指到隊尾。
5.將另外一個比較序列剩下的所有元素追加到合併序列的隊尾
 

歸併排序的直觀排序圖

程式碼實現

在貼程式碼段之前對於初學者來說到底該怎麼寫程式碼我覺得有必要說一下。程式碼真的不是一氣呵成的，而且也不是想當然寫出來的。
這個時候可能需要反覆斷點中斷來檢視是否有邏輯錯誤。在這裡建議大家包括我在內，在理解了問題的基礎下我們需要先把大體的程式碼框架最好先寫出來，特別是主要的邏輯判斷語句。
但是不需要太care我迴圈體或者判斷裡面語句怎麼實現，當你把這一步做到的時候能避免很多不必要的錯誤發生。在嘗試自己寫歸併排序的時候我也犯了剛剛的錯誤，下面貼上程式碼。

import random

def ConfiationAlgorithm(str):
    if
 
 len(str) <= 1: #子序列
        return str
    mid = (len(str) / 2)
    left = ConfiationAlgorithm(str[:mid])#遞迴的切片操作
    right = ConfiationAlgorithm(str[mid:len(str)]) 
    result = []
    #i,j = 0,0

    while len(left) > 0 and len(right) > 0:
        if (left[0] <= right[0]):
            #result.append(left[0])
            result.append(left.pop(0))
            #i+= 1
        else:
            #result.append(right[0])
            result.append(right.pop(0))
            #j+= 1

    if (len(left) > 0):
        result.extend(ConfiationAlgorithm(left))
    else:
        result.extend(ConfiationAlgorithm(right))
    return result   
if __name__ == '__main__':
    a = [20,30,64,16,8,0,99,24,75,100,69]
    print ConfiationAlgorithm(a)
    b = [random.randint(1,1000) for i in range(10)]
    print ConfiationAlgorithm(b)

這裡我打算是想用一個方法來實現歸併排序，這個方法裡面包含了三個部分：
第一個部分切片操作，
第二個部分比較操作，
第三個操作針對子序列多出來的數將追加到合併序列中。
但是一開始在第二部分比較的時候犯了很嚴重的錯誤就是一開始的時候條件沒有寫明白，導致我在迴圈體重填充程式碼的時候出現了各種各樣的錯誤，這種情況下只能斷點中斷來排查。
註釋的語句段就是我直接對切片的子序列做操作，然後沒有彈出比較完的數，導致第一遍迴圈直接死迴圈然後報錯。其實設i,j來比較子序列的數可以不可以，答案當然是可以的，當時問題就在於我這是一個方法。
要按照註釋裡面來寫的話其實我的迴圈條件是有問題的。在程式碼片中首先用left來切片包含兩個元素的子序列出來然後left,right最初都只有一個數通過比較之後完成了子序列的有序性。
然後我覺得非常有意思的就是兩個return的作用。如果不明白的童鞋可以斷點中斷來看看，分析分析。

時間複雜度

歸併排序是分治演算法的一種提現，按照分治算思想的童鞋來說可以很容易理解。
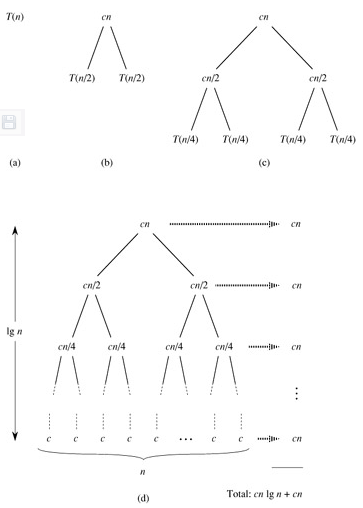
總時間=分解時間+解決問題時間+合併問題時間。在這裡分解問題的時間為一個常數，就是把一個待排序的序列分解成兩個序列，時間複雜度為O(1),解決問題的時間就是將一個規模為N的問題來遞迴成兩個規模為N/2的子問題，時間複雜度為2T(N/2)。
合併的時間複雜度只取決於你的深度O(N)。總時間T(N)=2T(N/2)+O(N)。在這裡我們略去繁瑣的數學證明來簡要的說一下。

把圖中所有的項加起來就是總的執行時間。這其實就是一顆完全二叉樹，每一層的和都是Cn，一共有log（n）+1層，因此總的執行時間Cnlog（n）+Cn，可得出時間複雜度為O（nlogn）。