接近assignment1的尾聲了，這次我們要完成的是一個兩層的神經網路，要求如下：

   RELU使用np.maximum()即可；

   Softmax與作業上個part相同，可以直接照搬。

   不同的地方在求導，兩個全連線層，共有W1 b1 W2 b2四個引數。對於它們具體的計算過程下面根據程式碼討論.

    1.前向傳播

out1 = X.dot(W1) + b1
relu = np.maximum(0, out1)
scores = relu.dot(W2) + b2 
#N為num_train
correct_class_score = scores[np.arange(N), y].reshape(N,1)
exp_sum = np.sum(np.exp(scores), axis = 1).reshape(N, 1)
loss = np.sum(np.log(exp_sum) - correct_class_score)
loss /= N
loss += 0.5 * reg * np.sum(W1 * W1) + 0.5 * reg * np.sum(W2 * W2)
 

    2.反向傳播

    首先是第二層的dW2 db2。先說b的導數，由於使用線性模型y = Wx + b，對b求偏導結果為1，因此把上游傳下來的值sum以下就行，無論那一層都是如此，因此db2就是對loss直接sum，dW2可直接套用Softmax結果。

p2 = np.exp(scores) / exp_sum
p2[np.arange(N), y] += -1
p2 /= N  #(N, C)
dW2 = relu.T.dot(p2)
dW2 += reg * W2
grads['W2'] = dW2
grads['b2'] = np.sum(p2, axis = 0)

     然後是第一層的dW1 db1。db1依然為上游傳的值求sum；然後利用鏈式法則，dW1的計算如下（真正的計算順序為X1PW2）,再注意中間加上relu層即可。

p1 = p2.dot(W2.T)
p1[relu <= 0] = 0
dW1 = X.T.dot(p1)
dW1 += reg * W1
grads['W1'] = dW1
grads['b1'] = np.sum(p1, axis = 0)

至此，neural_net.py基本完成，其餘部分比較簡單，之前也做過，這裡不再討論。

3.驗證與調參

驗證模型：①輸入給定值，計算與理論結果的誤差；②使用很小的資料集訓練，正常情況下loss可減小到0。

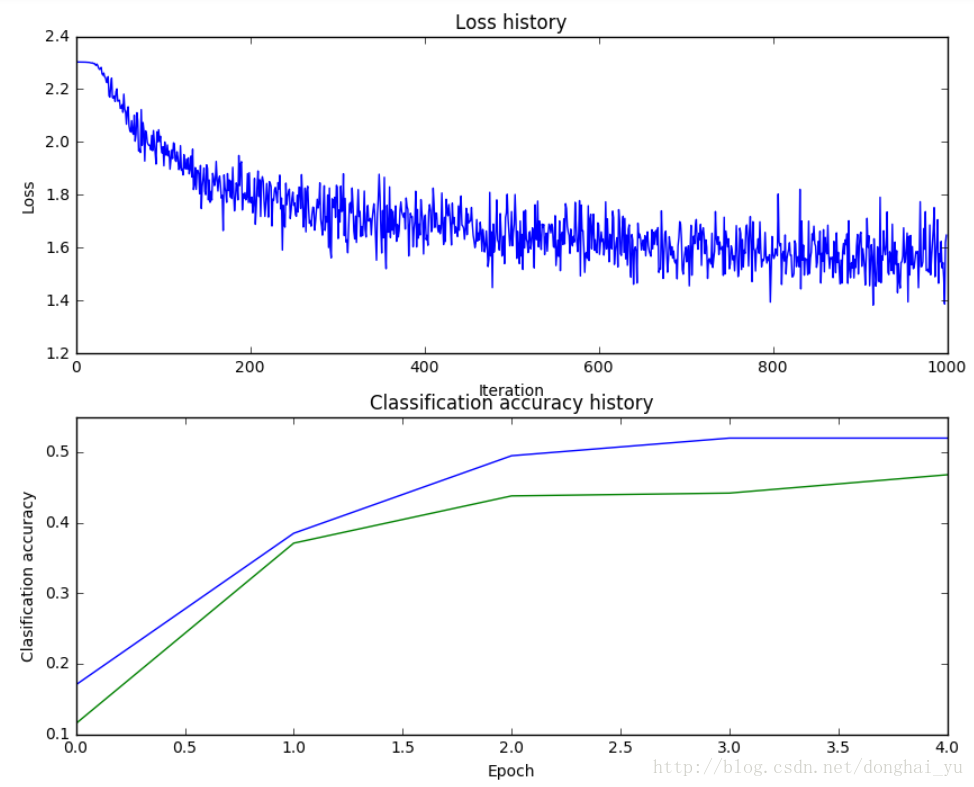
驗證正確後，根據題目給定的資料進行訓練，得到訓練結果如下：

      看loss的曲線，發現learning_rate還太低，可以提高；訓練集與驗證集的gap很小，可以在不過擬合的情況下考慮適當增大hidden layer的尺寸來得到更好的學習能力。還有可以考慮的超引數是epochs、regularization strength，此外一般來說增加迭代的次數會訓練得到更好的結果。最後，在使用預設learning rate decay也可獲得較好效果後，我們也可以嘗試進行調整。

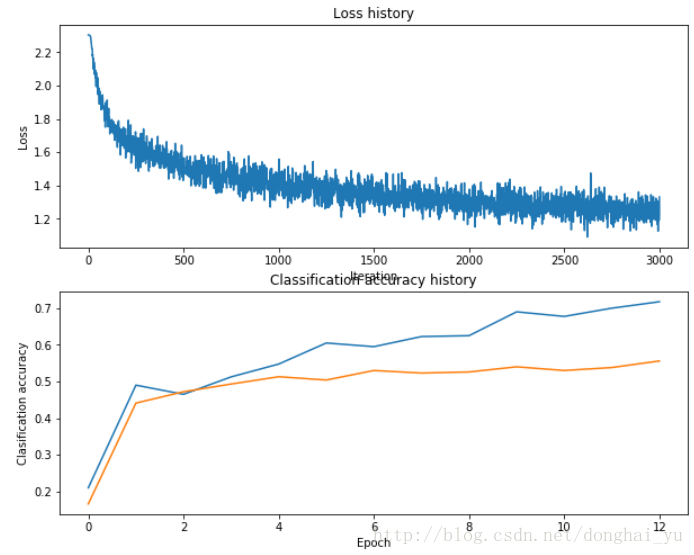
 以下是我調整的引數 

input_size = 32 * 32 * 3
hidden_size = 280
num_classes = 10
net = TwoLayerNet(input_size, hidden_size, num_classes)
# Train the network
stats = net.train(X_train, y_train, X_val, y_val,
            num_iters=3000, batch_size=400,
            learning_rate=1.6e-3, learning_rate_decay=0.9,
            reg=0.5, verbose=True)

       最終測試集的結果為：

       嘻嘻，拿到了3分的bonus.