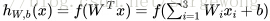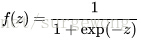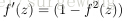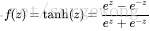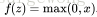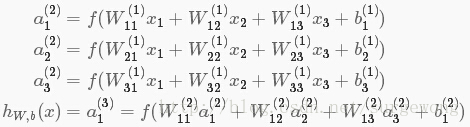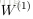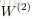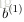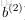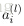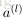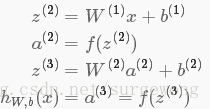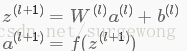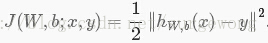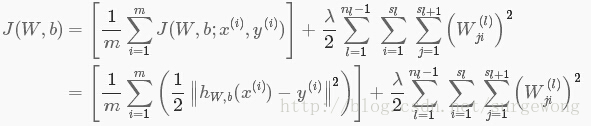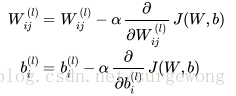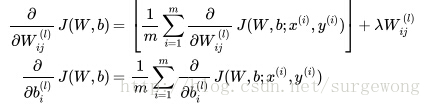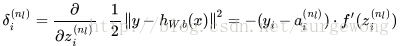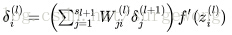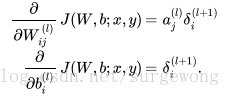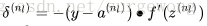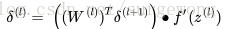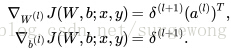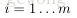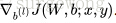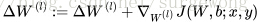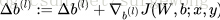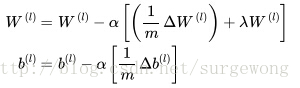Multi-Layer Neural Network     

[email protected]

http://blog.csdn.net/surgewong

       接觸機器學習有一段時間了，但是對於神經網路一直感覺比較“神祕”，再加之深度學習的概念炒得這麼熱，都不好意思說自己不懂神經網路了。本文主要是為了記錄自己對神經網路的理解以及一些心得，由於是一個新手，其中的一些理解不免有些錯誤，望各位能夠指正。本文主要參考 UFLDL Tutorial的同名教程【1】，在理解過程中主要參考了部落格，反向傳播BP演算法【2】。正如【2】所說【1】中變數的上下標比較多，理解起來可能有些不便，記得耐心看下去哦。

 一、初識神經網路 

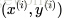
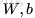
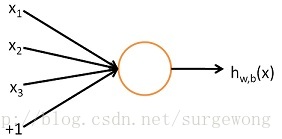
       給出一個監督學習的問題，輸入一系列的帶標籤的形如的訓練資料，神經網路可以給出一個複雜的、非線性的形如的模型，其引數為。所有的神經網路模型基本上就是圍繞這兩個引數展開的。

       先了解一下單個神經元（neuron）的網路。其實邏輯迴歸（Logistic Regression ）（不熟悉的同學可以參考【3】），就是一個單神經元網路。

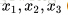
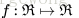
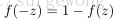
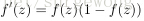
       上面的“網路”結構，輸入3個變數，外加一個截距（intercept）(+1)。輸出結果為：

，這裡的函式是激勵函式（activation function）【4】，最常用的激勵函式時sigmoid函式，採用它，那這個網路就變成了邏輯迴歸問題。sigmoid的函式有些很重要的特性，和。

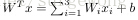
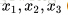
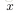
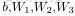
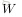
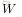
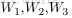
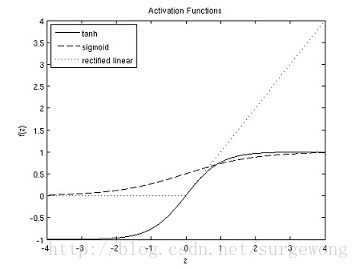
      剛接觸神經網路不久，對一些習以為常的概念感覺有點疑惑，在這裡記下自己對其的理解。上面用到公式 ，可以這樣理解，把1，看成變數的分量，變數看成是的分量（注意：與網路引數中的不同，網路中引數是指）。另外作為一個初學者，想必很想知道激勵函式的作用。激勵函式是對生物神經資訊處理的一種模擬，根據【4】裡的說法，非線性的激勵函式能夠使得網路系統使用較少的節點適應複雜的模型。激勵函式的作用有點類似與SVM中的核函式的作用，是對網路功能的一種擴充套件。

       sigmoid函式是最常用的激勵函式，除此之外還有雙曲正切函式（hyperbolic tangent），不過雙曲正切函式將值對映到(-1,1)，相比sigmoid就相當於將類別分為-1和1，可以認為是sigmoid函式的一種“拉伸”。雙曲正切函式的特性有：，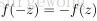

      最近的研究發現還有一種新的激勵函式，修正後的線性函式（rectified linear function），在小於0的部分，激勵函式輸出0，大於0的部分，輸出為 原來的值。與sigmoid函式和雙曲正切函式相比，該函式沒有限定其值域，並且該函式在0點出，不可導。

     下面給出的是sigmoid，tanh，修改後的線性函式的圖：

二、神經網路模型（Neural Network model）

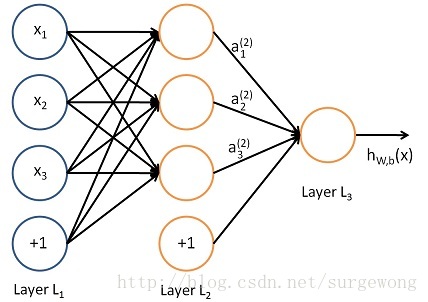
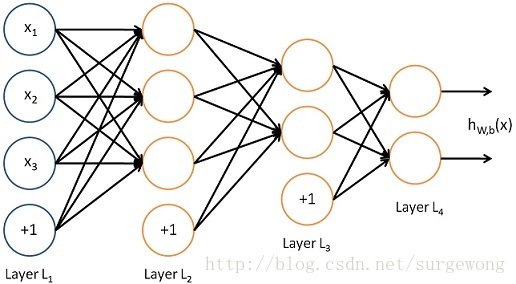
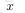
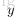
        下面考慮一個簡單地三層的網路結構，相比單個神經元網路結構而言只是增加了一箇中間隱層（hidden layer）。隱層（hidden）是相對於輸入（Input layer）和輸出層（Output layer）而言的，輸入層是指輸入的資料的各個分量，這個是可見的；輸出層是指輸出的值的分量（如果是1維，就相當於是一個分類問題）。

        上圖的網路結構中+1表示一個偏置（bias），也就是上面講的截距（intercept），這個雖然是網路中的一個節點，但是在說網路結構的時候，通常不將其計算在內。上圖中的網路結構可以描述成，三個輸入節點，三個隱藏節點，一個輸出節點。

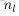
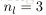
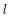
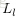
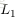
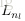
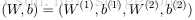
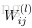
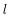
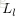
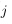
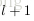
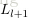
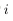
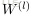
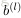
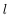
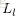
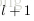
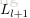
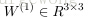
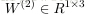
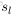
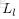
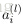
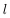
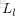
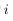
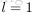
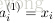
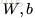
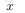
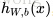
        為了描述這個網路結構，令網路層數為，在上述網路結構中。將第層表示成，那麼輸入層就是，輸出層就是。網路的引數可以表示成，這裡表示，從第層的第個節點到第層的第個節點的權值，和就是第層到第層的網路引數。網路中給出的輸入3個節點，隱層節點3個，輸出節點1個，有，。令為層中節點的個數（不包括偏置節點）。

        令為第層的第個節點經過激勵函式之後的輸出值。當時，有。給定輸入，根據網路結構，可以計算出網路輸出的結果為：

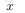
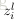
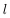
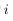
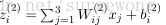
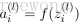
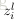
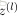
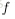
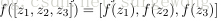
         上面的公式是的分量形式，在實際運算過程中，主要是通過矩陣和向量進行的。為了簡化公式，令為第層的第個節點輸入的和，例如，那麼就有。即便如此，仍然是單個值，是向量的分量。為此將激勵函式應用在向量上，也就是對向量的每個元素計算函式值，例如。這樣公式可以寫成：

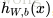
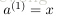
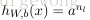
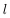
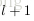
           接下來就可以通過矩陣和向量的操作得到網路的輸出結果，這個過程叫著前向傳播（forward propagation）。更一般地，令，，在第層和第層之間有：

           

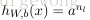
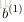
          上面我們給出最後的結果是1維，輸出多維的結果其實是一樣的，都有，只不輸出的最後一層的結果是對應的多維而已。同樣對應包含更多隱層的網路結構，也是類似的，因為其每一層之間的計算的方式都是類似的（請看上面的遞推公式）。還有每層的節點個數都是可以不同的，只是對應上面的遞推公式中變數的維數有所變化而已。在設計網路的過程中，可以選擇不同的網路層數，不同層數的節點個數，以及最後輸出結果的維數。它們所用的遞推公式都是相同的。

三、後向傳播演算法（Back Propagation Algorithm）

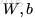
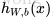
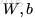
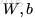
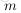
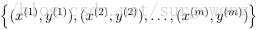
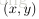
       上面介紹了前向傳播（forward propagation）的過程，也就是給定網路引數的情況下，通過網路結構計算得到最後的結果。很自然地就想知道如何計算得到網路引數。這裡就需要介紹後向傳播演算法（Back Propagation Algorithm），要了解這部分也可以參考【2】。

       網路引數是通過訓練得到的，假定有個元素的訓練集合，對與單個訓練樣本，其代價函式（cost function）為：

       對於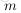個元素，定義總的代價函式為：

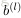
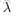
        這裡引入了一個正則項，主要是為了防止過擬合，從上面的公式可以看出，正則項中沒有偏置項，根據【1】中的理解，偏置項對網路最終的結果影響不大，所以就沒有考慮。（注：這裡沒有完全理解）正則項的係數為，主要是為了調節兩者的權重比值。

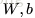
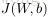
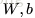
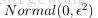
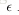
       在訓練過程，主要目的就是最小化自變數為的總代價函式。在網路的最初始階段，都是未知的，需要對其進行初始化，比較常用的初始化方法是將所有值初始化為零，但是總代價函式是一個非凸函式，使用梯度下降法很容易導致求解得到區域性最優解，而梯度下降法在實際網路求解過程中，效果都不錯，為了避免產生區域性最優解的情況，實際初始化方法一般採用正態分佈（一般較小，例如0.01）。如果初始化為同一個值，那麼相同隱層下的節點的輸出值都是相同的，不利於求解，採用正態分佈隨機的初始化主要是為了打破對稱性（symmetric breaking）。

       使用梯度下降法更新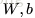，來求解得到結果，其計算公式為：

       公式中的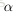是學習率，簡單說來就是小的增量。下面公式給出了上面兩個偏導函式的求解方法：

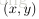
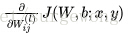
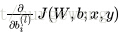
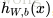
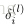
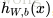
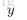
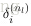
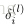
       進一步問題簡化了：在單個樣本下，，的計算問題。這裡用到就是後向傳播（Back Propagation Algorithm）演算法。演算法的大致思路：在初始化的網路中，使用前向傳播，計算，然後計算每層的每個節點的誤差（其實就是偏導），這個值代表與“真實結果”的差。很容易通過比較，獲取最後輸出結果的，最關鍵的就是計算隱層中。後向傳播演算法的步驟：

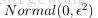
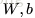
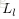
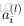
        1. 使用初始化網路引數，計算每一層的輸出每個節點的輸出，直到最後一層

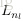
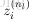
        2. 對於輸出層（層），計算每個節點相對於輸入的誤差：

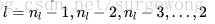
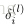
        3. 對於隱層，中的每一個節點誤差，這裡是將後面一層的誤差傳播到前面一層，前面一層通過連線的權值將這些誤差累計起來：

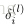
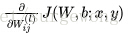
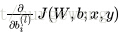
        4. 計算得到每層的每個節點的，就可以計算和了：

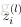
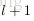
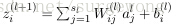
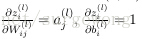
        怎麼理解上述中的兩個公式呢？還記得的定義麼？為了更加容易理解，這裡給出第的求解公式，求偏導有，使用鏈式規則很容易得到上面的結果。

        上面得到的結果是單個分量的形式，下面將其表達成矩陣和向量形式。將激勵函式的導數應用於向量的每個元素，類似的有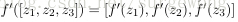：。同時用表示向量或矩陣的元素之間的乘法，而不是矩陣運算，相當於matlab中的點乘。於是上面的反向傳播演算法可以表述為：

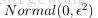
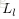
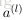
        1. 使用初始化網路引數，計算每一層的輸出向量，直到最後一層

        2. 對於輸出層（層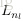），計算每層的誤差向量：

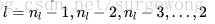
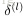
        3. 對於隱層，中的層的誤差向量，

        4. 計算得到每層的 誤差向量，就可以計算每層引數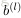的梯度了：

   

四、演算法實現

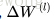
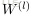
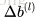
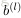
       首先定義為的各個元素變化構成的矩陣，為的各個元素變化構成的矩陣。那麼實現步驟如下

       1. 初始化網路，，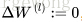

       2. 對於

           使用後向傳播演算法計算和

           更新，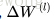

           更新，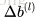

      4. 最後跟新

       本文基本上算是對【1】的翻譯和註釋，現在基本上算是整理清楚了網路的結構，可以進行下一步的學習了。下面附上UFLDL教程下，matlab的實現程式碼。由於是MNIST手寫數字是一個多分類問題，最後一層使用的損失函式和Softmax的類似，與上文中的二次損失函式不同，在程式碼supervised_dnn_cost.m的實現部分需要注意。另外程式碼可以參考【5】。

function [ cost, grad, pred_prob] = supervised_dnn_cost( theta, ei, data, labels, pred_only)
%SPNETCOSTSLAVE Slave cost function for simple phone net
%   Does all the work of cost / gradient computation
%   Returns cost broken into cross-entropy, weight norm, and prox reg
%        components (ceCost, wCost, pCost)

%% default values
po = false;
if exist('pred_only','var')
  po = pred_only;
end;

%% reshape into network
stack = params2stack(theta, ei);
numHidden = numel(ei.layer_sizes) - 1;
hAct = cell(numHidden+1, 1);
gradStack = cell(numHidden+1, 1);
% stack 記錄著網路的引數W1,b1;W2,b2(這是隱層數為1的結果，多層的情況類似)
% numHidden 隱層的數目
% hAct 網路每一層的輸入與輸出結果（輸入層除外）(為了更清楚地瞭解神經網路的執行過程，下面的計算過程，每層的中間結果都儲存在這個節點中)
% gradStack 訓練網路的梯度

%% forward prop
for l = 1:numHidden+1
    if(l == 1)
        hAct{l}.z = stack{l}.W*data;  % 第一個隱層，將訓練資料集作為其資料
    else
        hAct{l}.z = stack{l}.W*hAct{l-1}.a; % 第l層的輸入，是第l-1層的輸出，
    end
    hAct{l}.z = bsxfun(@plus,hAct{l}.z,stack{l}.b); % 第l層的節點的輸入加上偏置
    hAct{l}.a = sigmoid(hAct{l}.z); % 應用啟用函式
end

% 預測概率為softmax方式，可能由於框架的原因，使用二次損失函式計算出來的效果不是很好
total_e = exp(hAct{numHidden+1}.z);
pred_prob = bsxfun(@rdivide,total_e,sum(total_e,1));
hAct{numHidden+1}.a = pred_prob;

%% return here if only predictions desired.
if po
  cost = -1; ceCost = -1; wCost = -1; numCorrect = -1;
  grad = [];  
  return;
end;

%% compute cost
% 使用softmax方法，計算J(W,b),最後一個層的輸出結果就是hw,b(x) = hAct{numHidden+1}.a
label_index = sub2ind(size(hAct{numHidden+1}.a),labels',1:size(hAct{numHidden+1}.a,2));
ceCost = -sum(log(hAct{numHidden+1}.a(label_index)));   % softmax 的方式計算損失函式，不帶正則項

%% compute gradients using backpropagation
% 計算每層輸出的誤差（對輸入z的偏導）
% sigmoid的導函式 f'(z) = f(z)(1-(f(z)))
% a = f(z) 
tabels = zeros(size(hAct{numHidden+1}.a));
tabels(label_index) = 1;
for l = numHidden+1:-1:1 
    if(l == numHidden+1)
        hAct{l}.delta = -(tabels - hAct{l}.a);  % 輸出層使用softmax的損失函式，所以和二次項損失函式不同，其他的都是一樣的
    else
        hAct{l}.delta = (stack{l+1}.W'* hAct{l+1}.delta) .* (hAct{l}.a .*(1- hAct{l}.a));
    end
    
    if(l == 1)
        gradStack{l}.W = hAct{l}.delta*data';
        gradStack{l}.b = sum(hAct{l}.delta,2);
    else
        gradStack{l}.W = hAct{l}.delta*hAct{l-1}.a';
        gradStack{l}.b = sum(hAct{l}.delta,2);        
    end    
end


%% compute weight penalty cost and gradient for non-bias terms
wCost = 0;
for l = 1:numHidden
    wCost = wCost+ sum(sum(stack{l}.W.^2));   %  網路引數W 的累計和,正則項損失
end
cost = ceCost + .5 * ei.lambda * wCost; % 帶正則項的損失

% Computing the gradient of the weight decay.
for l = numHidden+1: -1 : 1
    gradStack{l}.W = gradStack{l}.W + ei.lambda * stack{l}.W;
end

%% reshape gradients into vector
[grad] = stack2params(gradStack);
end

【1】UFLDL：Multi-Layer Neural Network

【2】CSDN：反向傳播BP演算法

【3】UFLDL：Logistic Regression

【4】Wikipedia：activation function

【5】CSDN：ufldl學習筆記與程式設計作業：Multi-Layer Neural Network