解決離群值得方法有很多簡單來說一下--箱形圖-

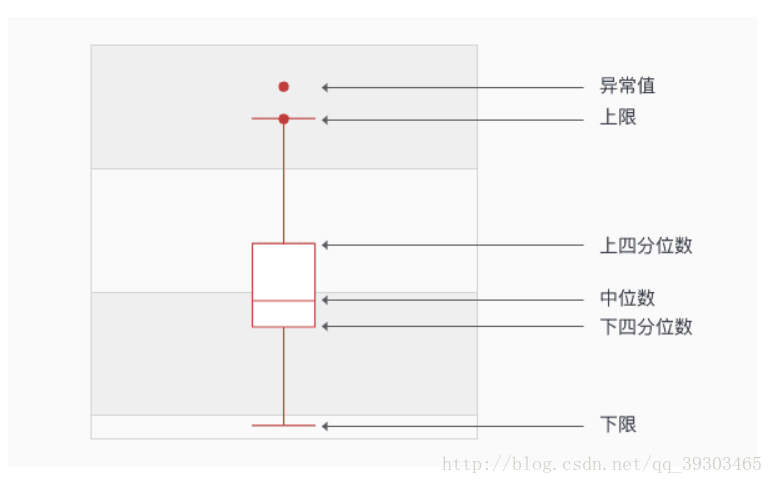
箱形圖（英文：Box plot），又稱為盒須圖、盒式圖、盒狀圖或箱線圖，是一種用作顯示一組資料分散情況資料的統計圖。因型狀如箱子而得名。在各種領域也經常被使用，常見於品質管理，快速識別異常值。

箱形圖最大的優點就是不受異常值的影響，能夠準確穩定地描繪出資料的離散分佈情況，同時也利於資料的清洗

想要搞懂箱形圖，那麼一定要了解...

五大因“數”

1、下四分位數Q1

（1）確定四分位數的位置。Qi所在位置=i（n+1）/4，其中i=1，2，3。n表示序列中包含的項數。

（2）根據位置，計算相應的四分位數。

例中：

Q1所在的位置=（14+1）/4=3.75，

Q1=0.25×第三項+0.75×第四項=0.25×17+0.75×19=18.5；

2、中位數（第二個四分位數）Q2

中位數，即一組數由小到大排列處於中間位置的數。若序列數為偶數個，該組的中位數為中間兩個數的平均數。

例中：

Q2所在的位置=2（14+1）/4=7.5，

Q2=0.5×第七項+0.5×第八項=0.5×25+0.5×28=26.5

3、上四分位數Q3

計算方法同下四分位數。

例中：

Q3所在的位置=3（14+1）/4=11.25，

Q3=0.75×第十一項+0.25×第十二項=0.75×34+0.25×35=34.25。

4、上限

上限是非異常範圍內的最大值。

首先要知道什麼是四分位距如何計算的？

四分位距IQR=Q3-Q1，那麼上限=Q3+1.5IQR

5、下限

下限是非異常範圍內的最小值。

下限=Q1-1.5IQR

講了這麼多的“數學知識”，那麼箱形圖到底如何通過BDP應用到實際的工作呢？我們還是用一個例項來幫助大家理解。

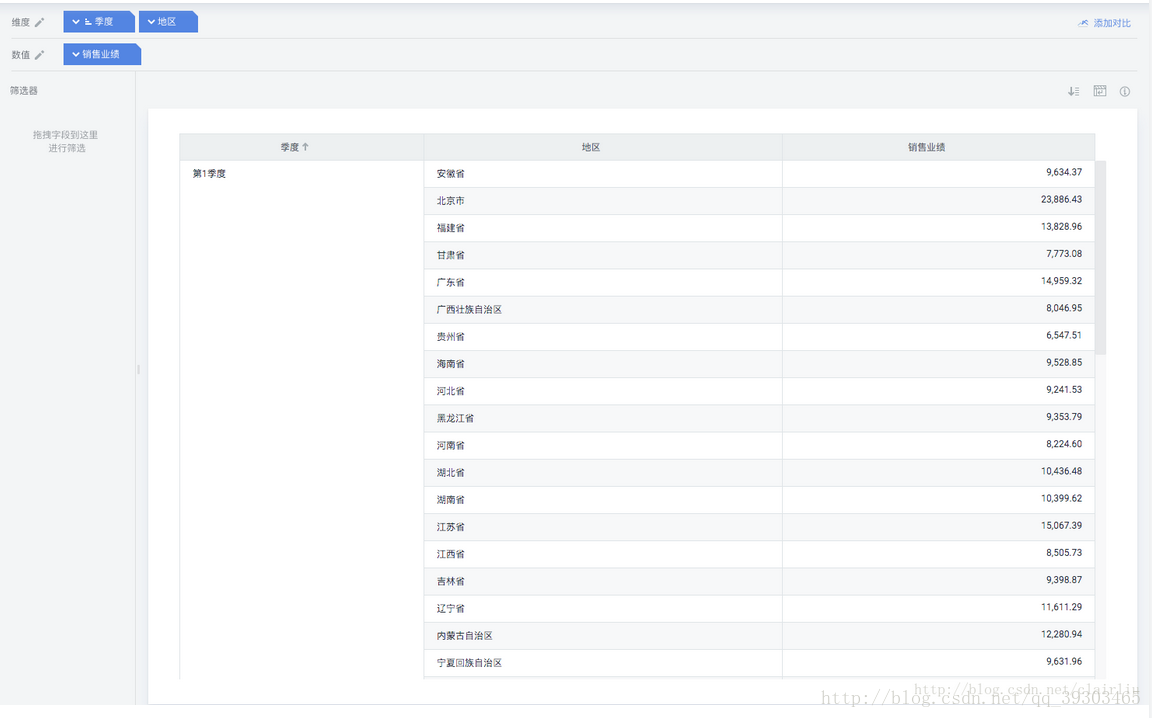
現在有“2017年各季度各地區分公司銷售業績”工作表，我們想要找出各季度哪些分公司業績屬於不正常範圍內。

資料示例如下圖：

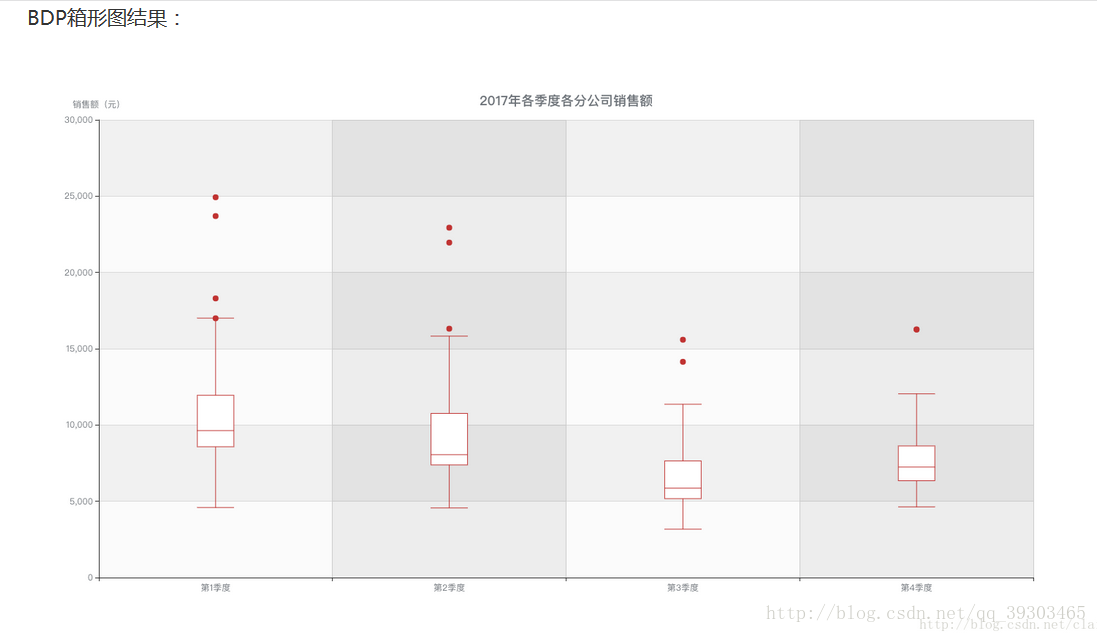
從上圖可以清晰的找出異常點，例如第二季度北京分公司的銷售額為22147元，該值比上限10759元還要大，所以定義為異常值。

箱形圖的價值

1.直觀明瞭地識別資料批中的異常值

上文講了很久的識別異常值，其實箱線圖判斷異常值的標準以四分位數和四分位距為基礎，四分位數具有一定的耐抗性，多達25%的資料可以變得任意遠而不會很大地擾動四分位數，所以異常值不會影響箱形圖的資料形狀，箱線圖識別異常值的結果比較客觀。由此可見，箱線圖在識別異常值方面有一定的優越性。

2.利用箱線圖判斷資料批的偏態和尾重

對於標準正態分佈的樣本，只有極少值為異常值。異常值越多說明尾部越重，自由度越小（即自由變動的量的個數）；

而偏態表示偏離程度，異常值集中在較小值一側，則分佈呈左偏態；異常值集中在較大值一側，則分佈呈右偏態。

3.利用箱線圖比較幾批資料的形狀

同一數軸上，幾批資料的箱線圖並行排列，幾批資料的中位數、尾長、異常值、分佈區間等形狀資訊便昭然若揭。如上圖，可直觀得看出第三季度各分公司的銷售額大體都在下降。

但箱形圖也有他的侷限性，比如：不能精確地衡量資料分佈的偏態和尾重程度；對於批量比較大的資料，反映的資訊更加模糊以及用中位數代表總體評價水平有一定的侷限性。