評判演算法的標準

• 時效高和儲存低
• 「時效」是指時間效率，也就是演算法的執行時間
• 「儲存」是指演算法在執行的時候需要的儲存空間

時間複雜度(一般是最壞情況下的時間複雜度)

根據數量級，描述時間複雜度，一般用「大 O」表示，記做 O(f(n)),n為資料的規模

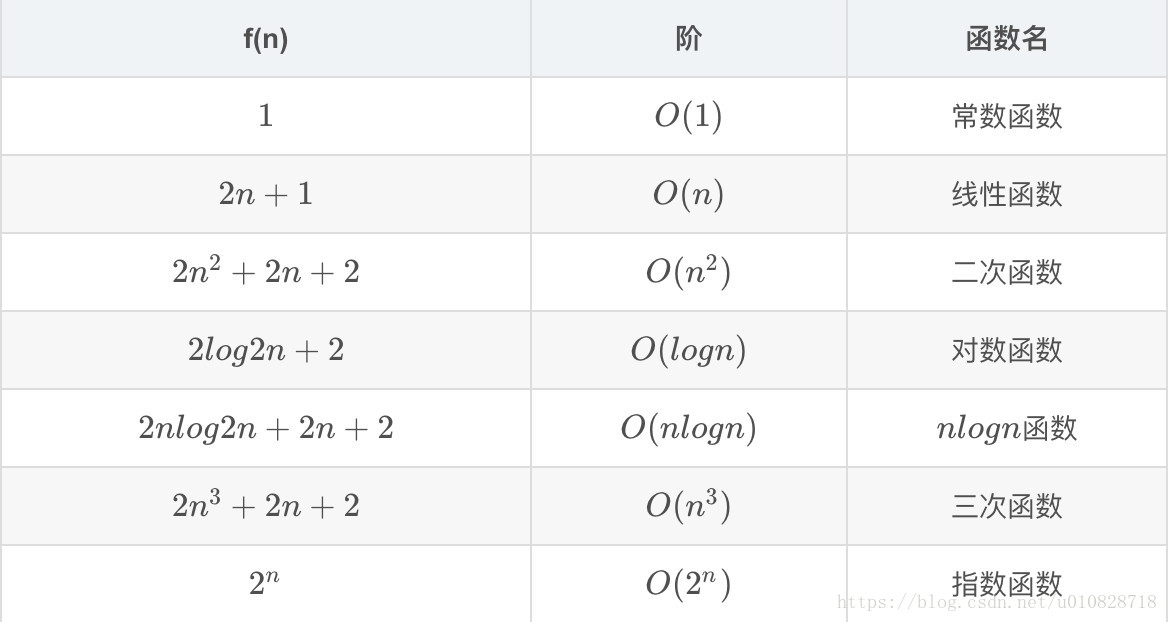
常見數量級函式

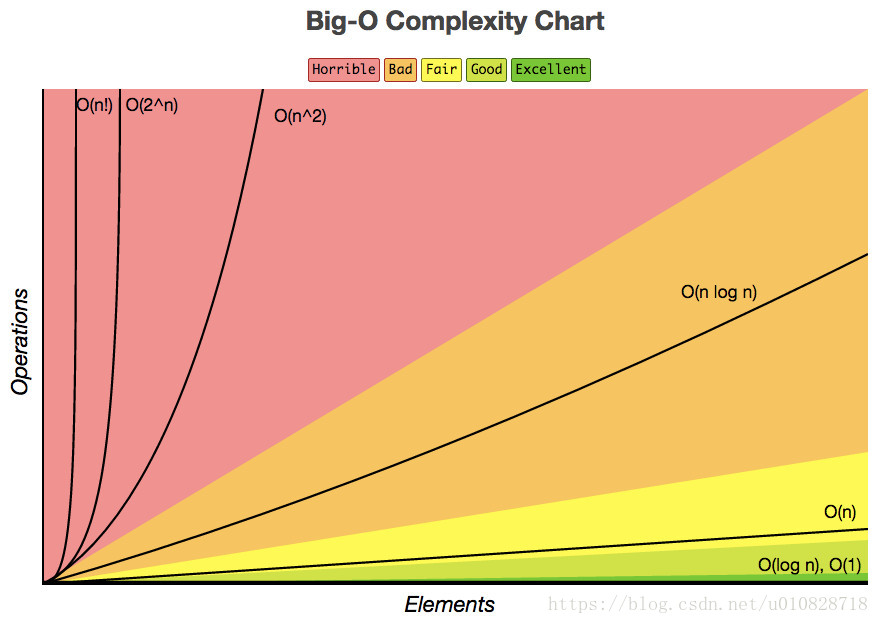
當 n 增大時，數量級函式增長幅度排名

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n)

1.常數函式

n = 100  # 1 次
sum  = (1 + n) *n / 2 # 1 次
print(sum)
 
 # 1 次

上面的演算法程式的時間複雜度就是 O(1)

無論 n 為多少，程式碼就是 執行 3 次。這種與資料的規模大小 n 無關，執行時間恆定的演算法我們就叫它具有 O(1) 的時間複雜度。

2.對數函式

cnt = 1
while cnt < n:
   cnt *= 2 # O(1)

上面的演算法程式的時間複雜度就是 O(logn)

上述的程式碼可以解釋成 cnt 乘以多少個 2 以後才能大於等於 n，我們假設個數是 x，也就是求 2^x = n，即 x = log2n，所以這個迴圈的時間複雜度就是 O(logn)。

3.綜合

a = 1
b = 2
c = 3

for
 
 i in range(n):
   for j in range(n):
       x = i * i
       y = j * j
       z = i * j

for k in range(n):
   u = a * k + b
   v = c * c

d = 4

上面程式的時間複雜度就是 O(n^2)

可以分成 4 部分：
第 1 部分是 a，b，c 這 3 個賦值語句，執行次數也就是 3 次；
第二部分是 3n^2，因為是迴圈結構，裡面有 x，y，z 這 3 個賦值語句，每個語句執行了 n^2 次；
第 3 部分是 2n，因為裡面是 2 個賦值語句，每條語句被執行了 n 次；
第 4 部分是常數 1，只有 d 這麼 1 條賦值語句。
所以我們得到的 T(n) = 3+3n^2 +2n+1 = 3n^2+2n+4，看到指數項，我們自然的發現是 n^2 做主導，當 n 增大時，後面兩項可以忽略掉，所以這個程式碼片段的數量級就是 O(n^2)

空間複雜度

演算法所耗費的儲存空間，計算公式計作：S(n) = O(f(n))。其中 n 也為資料的規模，f(n) 在這裡指的是 n 所佔儲存空間的函式。

一般情況下，我們的程式在機器上執行時，刨去需要儲存程式本身的輸入資料等之外，還需要儲存對資料操作的「儲存單元」。如果輸入資料所佔空間和演算法無關，只取決於問題本身，那麼只需要分析演算法在實現過程中所佔的「輔助單元」即可。如果所需的輔助單元是個常數，那麼空間複雜度就是 O(1)。

空間複雜度其實在這裡更多的是說一下這個概念，因為當今硬體的儲存量級比較大，一般不會為了稍微減少一點兒空間複雜度而大動干戈，更多的是去想怎麼優化演算法的時間複雜度。所以我們在日常寫程式碼的時候就衍生出了用「空間換時間」的做法，並且成為常態。比如我們在求解斐波那契數列數列的時候我們可以直接用公式去遞迴求，用哪個求哪個，同樣也可以先把很多結果都算出來儲存起來，然後用到哪個直接呼叫，這就是典型的用空間換時間的做法，但是你說這兩種具體哪個好，偉大的馬克思告訴我們「具體問題具體分析」。