評價一般用來評估某件事物的成績、水平或程度。通常每個個體都有多個不同的指標去衡量，除開資料的預處理之外，評價的過程可分為三大步：

    一對於每個指標給每個個體打分；

    二賦予每個指標一個權重；

    三根據權重將指標得分綜合起來，從而獲得該個體的綜合評價。

    常見的評價演算法有：TOPSIS理想解法、模糊綜合評價、層次分析法、熵權法、秩和比綜合評價、灰色關聯分析、粗糙集綜合評價、主成分分析法等。這些演算法根據上面的三個步驟可以分為客觀評價和主觀評價兩個大類。

Step1 首先是指標的給分，除非國際或者相關領域有著標準的給分，比如：每一級水質中各成分的含量都有一個標準，那麼根據這個標準，我們就可以將各個成分指標劃分到各自的級別。除開這種有標準的情況，評價演算法中還有所謂的專家打分

機制（其實大多數情況也是自己打分的，即自己給每個指標一個評分標準，然後根據這個人造標準來打分zz），從而完成第一步，使用這種專家打分方法的有模糊綜合評價、層次分析法、秩和比綜合評價、粗糙集法。

        當然也有客觀的評分機制，比如說TOPSIS理想解法和灰色關聯度法，這兩種方法是將每個指標中的最好資料合併，作為理想解，然後比較各個樣本與它的距離或者相關性，從而進行評價。

        Step2 接下來就是指標權重的確定，同樣也分為主觀定權和客觀定權兩種，上一步說的TOPSIS理想解法和灰色關聯度法沒有這一步，所以不考慮。
       主觀定權的方法有層次分析法、模糊綜合評價、秩和比綜合評價，看起來好像跟上一步主觀定權的一樣，但是還有一個方法在這一步變成了客觀定權，即粗糙集綜合評價，因為這個方法可以通過一個公式計算出每個指標的有無對結果的影響，從而確定每個指標的權重。
       關於客觀定權

，還有熵權法（指標內資料結構越複雜權重越大）、主成分分析。

       主成分分析（通過對多個指標的不同加權組合來表達原資料的結構，即降維，每個組合的貢獻率就是其權重），這類演算法的定權方式實質上就是如果某一指標內個樣本的區別越大，該指標的權重就越大。

       Step3 最後一步是綜合評價，就是將第一步各指標的分數與第二步的權重進行加權平均，就可以得到最終的評價。後文將以模糊綜合評價為例進行講解。

       以上這些演算法在比賽中可以嘗試進行組合，因為前兩個步驟都存在主客觀的問題，所以可以嘗試用專家打分方法完成第一步，客觀定權方法完成第二步。

       正如我在前文所說到的，在做評價問題時，我們可以利用客觀定權和主觀評分

的方式來進行評價，這樣的合理性和效果往往會比單一方法的效果好。這裡，我就拿熵權法和模糊綜合評價的結合來講，不過該例子中評價步驟經常用於對個體的評價，而很少用於對多個個體的評價排序，如果想用可以修改一下過程。

例：現有一面試小組對某人知識面、理解能力、應變能力和表達能力的評價表，請根據此表給此人一個綜合評價。

•  確定因素集，這裡已經有現成的四個評價指標了，即知識面，應變能力，表達能力和理解能力；
  
•  確定評語集，這裡就需要我們自己劃分等級了，比如說最簡單的：
•  確定各因素權重，這裡我們採用熵權法進行客觀定權：
  

          第一步，資料標準化，即去除資料量綱，所以我們要將每一個指標下的10所有10個數據轉化到[0,1]之間，用的公式是：

          第二步，根據資訊熵公式計算各指標的資訊熵（如果p值為0，那麼plnp=0）：

           第三步，根據指標權重計算公式公式計算各指標的權重：

           到這一步，各指標的資訊熵和權重就得到了：

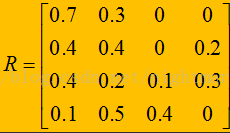
•  確定模糊綜合判斷矩陣，這一步我們先要將每個分數劃分到各自的等級中，因此該評分表可以改成：

       由此可得模糊綜合判斷矩陣：

      這個矩陣應該一行行去理解，比如說第一行，這代表著知識面這一指標中有70%的人認為此人的等級為A,30%的人認為此人的等級為B，以此類推可得。

• 模糊綜合評判，這一步我們直接將上面的矩陣與權重合成運算.

     可以發現0.3741最大，也就是說此人在等級B的隸屬度最高，因此最終給此人評價為B。