A、使用卷積進行特徵提取

一、概述

       在前面的練習中，你解決了畫素相對較低的影象的相關問題，例如小的圖片塊和手寫數字的小影象。在這個節，我們將研究能讓我們將這些方法拓展到擁有較大影象的更加實際的資料集的方法。

二、全連線網路

       在稀疏自編碼器中，我們所做的設計選擇是將所有隱藏層單元與輸入單元全部連線。在我們處理的相對小的影象中（例如在稀疏自編碼器作業中的8×8小塊，MNIST資料集中的28×28影象），學習整幅影象的特徵在計算上是非常靈活的。然而，對於大一點的影象（例如96×96影象），學習涵蓋在整幅影象上的特徵（全連線網路）在計算上是代價非常高——你將有大約10⁴個輸入單元，假設你想學習100個特徵，你將依次學習10⁶

三、區域性連線網路

       這個問題的一個簡單解決方法是限制隱藏層單元和輸入單元的連線，只允許隱藏單元與輸入單元的小的子集相連線。具體而言，每個隱藏單元只與輸入的小的一塊鄰域畫素相連線。（對於與影象不同的輸入形式，通常也有一種自然的方法選擇輸入單元的“鄰組”來與一個隱藏單元連線；例如，對於音訊，一個隱藏單元可以只與相當於某一時間長度的輸入音訊片段的輸入單元相連線。）

       這個區域性連線網路的想法也是從生物學中初期的視覺系統如何構建得到的靈感。具體而言，視覺皮層上的神經元有區域性感受野（即，它們只對某一個區域的刺激作出反應）。

四、卷積

       自然影象有一個叫“不變性”的特點，意思是影象某一部分的統計特性和其它部分是一樣的。這暗示著我們在某一部分學習到的特徵也能應用到影象的其它部分，所以我們可以在所有的區域都用相同的特徵（所以可以用相同的特徵篩選器，這裡在說權值共享）。

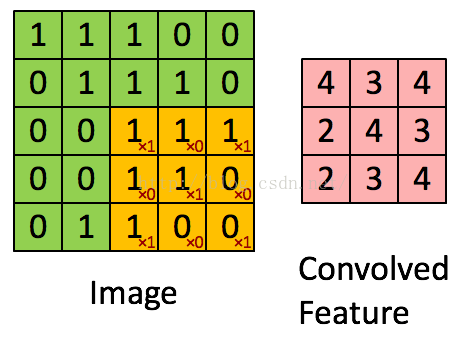
       更精確地說，在一幅大影象中隨機取樣的小塊（例如8×8）上學習了特徵後，我們可以將這塊訓練的8×8小塊作為特徵檢測器應用到影象的任何地方。具體而言，我們可以拿訓練的8×8特徵（檢測器）與大點的影象“卷積”，於是在影象的各個區域得到不同的特徵啟用值。

       為了給個具體的例子，假設你已經在從96×96的影象取樣得到的8×8小塊上學習了特徵。進一步假設這是由含100個隱藏單元的自動編碼器完成的（就像自動編碼器學習特徵一樣，假設要學100

       正式的說，給定一些r×c影象xlarge，我們首先在從這些影象中取樣的a×b小塊xsmall中訓練一個稀疏自動編碼器（k個隱藏單元），利用從視覺化單元到隱藏單元得到的權重W(1)和偏置b(1)，學習到k個特徵f=σ(W(1)xsmall+b(1))（其中σ是sigmoid函式）。對大影象的每個a×b小塊xs，我們計算fs=σ(W(1)xs+b(1))，得到fconvolved，一個k×(r−a+1)×(c−b+1)的卷積特徵。

       （上面那段最主要的意思應該是下面那幅圖：

兩個訊息：

1、 多卷積核——多通道，一個卷積核一個特徵；

2、 每個通道權值共享。

）

       在下一節，我們會深入描述如何一起“池化”這些特徵來得到甚至更好的特徵用來分類。

B、池化

一、概述

       使用卷積得到特徵後，我們接下來想用它們分類。在理論上，分類器可以使用所提取的所有特徵例如softmax分類器，但這在計算上充滿挑戰。例如對96×96畫素的影象考慮，假設我們已經在8×8的輸入學習了400種特徵。每個卷積結果的輸出大小為(96−8+1)∗(96−8+1)=7921，而且既然我們有400種特徵，每個例項將得到89²∗400=3,168,400的特徵向量。由擁有三百多萬特徵的輸入來學習分類器是很難處理的，而且容易過擬合。

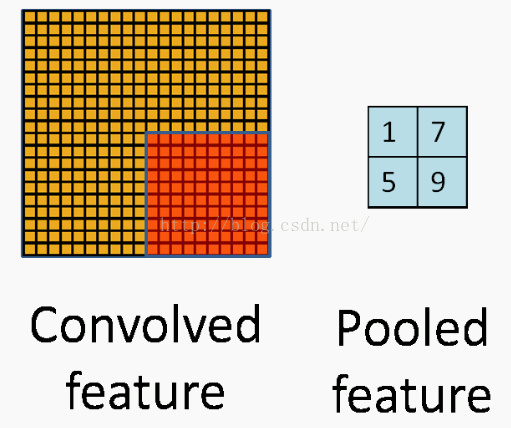
       為對付這種情況，首先回憶，我們決定得到卷積後的特徵是因為影象有“不變”的特性，它意味著在一個區域有用的特徵在其它地方也可能有用。因此，為了描述一副大影象，一個自然的方法是總結在不同區域的統計特徵。例如，可以計算影象中某一區域的特定特徵的平均（或最大）值。這些總結的統計特性在維度上小很多（與使用所有提取到的特徵比起來），也可以改善結果（減少過擬合的可能）。我們總結的操作稱為“池化”操作，或者有時候稱“平均池化”或“最大值池化”（取決於應用的池化操作方式）。

       下圖展示瞭如何在影象的4個非重疊區域做池化。

二、池化得到不變性

       如果選擇影象的連續區域作為池化區域並且只池化從相同的（重複的）隱藏單元得到的特徵，那麼這些池化單元具有“平移不變性”。這意味著相同的（池化的）特徵被激活了，即使影象作了（小的）平移。平移不變特徵經常是需要的；在許多工中（例如目標檢測，語音識別），即使影象平移了，例項（影象）的標籤是相同。例如，如果你拿到MNIST數字並將它向左或向右平移，你想讓你的分類器依舊能準確地將它歸為同一類，不管它們最終位置在哪裡。

三、正式說明

       正式地說，在得到我們之前描述的卷積特徵後，我們決定用大小例如m×n的區域，池化我們的卷積特徵。然後，我們將我們的卷積特徵分成不想交的m×n區域，然後在這些區域取平均（或最大）的特徵啟用值得到池化後的卷積特徵。這些池化後的特徵可以用作分類。