全排列的實現方法--遞迴&字典序
一:背景
全排列在很多筆試都有應用,是一個很常見的演算法,關於這類的題目變化很多。這種演算法的得到基於以下的分析思路。 給定一個具有n個元素的集合(n>=1),要求輸出這個集合中元素的所有可能的排列。
例如:給定{1,2,3},全排列為3!個,即:
{1,2,3},{1,3,2}
{2,1,3},{2,3,1}
{3,1,2},{3,2,1}
下來分別說下遞迴法,字典序演算法來實現全排列。
二:實現演算法
1.遞迴法
遞迴的話就很簡單了,以{1,2,3}為例,它的排列是:
以1開頭,後面接著{2,3}的全排列,
以2開頭,後面接著{1,3}的全排列,
以3開頭,後面接著{1,2}的全排列。
程式碼如下:
#include<iostream> #include<algorithm> using namespace std; int arry[3] = { 1,2,3 }; void Recursion(int s, int t) { if (s == t) for_each(arry, arry + 3, [](int i) {printf("%d", i); }), printf("\n"); else { for (int i = s; i <= t; i++) { swap(arry[i], arry[s]); Recursion(s + 1, t); swap(arry[i], arry[s]); } } } int main() { Recursion(0, 2); return 0; }
2.字典序演算法
首先看什麼叫字典序,顧名思義就是按照字典的順序(a-z, 1-9)。以字典序為基礎,我們可以得出任意兩個數字串的大小。比如 "1" < "12"<"13"。 就是按每個數字位逐個比較的結果。對於一個數字串,“123456789”, 可以知道最小的串是 從小到大的有序串“123456789”,而最大的串是從大到小的有序串“*987654321”。這樣對於“123456789”的所有排列,將他們排序,即可以得到按照字典序排序的所有排列的有序集合。
如此,當我們知道當前的排列時,要獲取下一個排列時,就可以範圍有序集合中的下一個數(恰好比他大的)。比如,當前的排列時“123456879”, 那麼恰好比他大的下一個排列就是“123456897”。 噹噹前的排列時最大的時候,說明所有的排列都找完了。
於是可以有下面計算下一個排列的演算法:
設P是1~n的一個全排列:p=p1p2......pn=p1p2......pj-1pjpj+1......pk-1pkpk+1......pn
1)從排列的右端開始,找出第一個比右邊數字小的數字的序號j(j從左端開始計算),即 j=max{i|pi<pi+1}
2)在pj的右邊的數字中,找出所有比pj大的數中最小的數字pk,即 k=max{i|pi>pj}(右邊的數從右至左是遞增的,因此k是所有大於pj的數字中序號最大者)
3)對換pi,pk
4)再將pj+1......pk-1pkpk+1......pn倒轉得到排列p'=p1p2.....pj-1pjpn.....pk+1pkpk-1.....pj+1,這就是排列p的下一個排列。
證明:
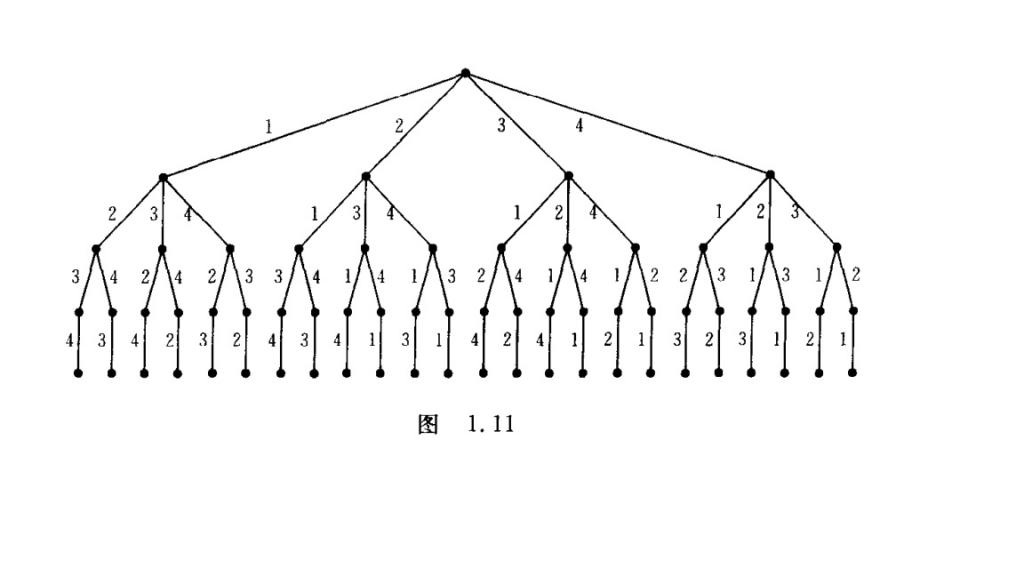
要證明這個演算法的正確性,我們只要證明生成的下一個排序是恰好比當前排列大的一個序列即可。圖1.11是從盧開澄老師的《組合數學》中擷取的一個有1234生成所有排序的字典序樹。從左到右的每一個根到葉子幾點的路徑就是一個排列。下面我們將以這個圖為基礎,來證明上面演算法的正確性。
演算法步驟1,得到的子串 s = {pj+1,.....,pn}, 是按照從大到小進行排列的。即有 pj+1 > pj+2 > ... > pn, 因為 j=max{i|pi<pi+1}。
演算法步驟2,得到了最小的比pj大的pk,從n往j數,第一個比j大的數字。將pk和pj替換,保證了替換後的數字比當前的數字要大。於是得到的序列為p1p2...pj-1pkpj+1...pk-1pjpk-1...pn.注意這裡已經將pk替換成了pk。這時候我們注意到比p1..pj-1pk.....,恰好比p1....pj.....pn大的數字集合。我們在這個集合中挑選出最小的一個即時所要求的下一個排列。
演算法步驟3,即是將pk後面的數字逆轉一下(從從大到小,變成了從小到大。)
由此經過上面3個步驟得到的下個排列時恰好比當前排列大的排列。
同時我們注意到,當所有排列都找完時,此時數字串從大到小排列。步驟1得到的j < 0,演算法結束。
程式碼如下:
#include<iostream>
#include<algorithm>
using namespace std;
int arry[3] = { 1,2,3 };//len==3;
void Permutation()
{
int len = 3;
int j, k;
while (true)
{
printf("%d%d%d\n", arry[0], arry[1], arry[2]);
for (j = len - 2; j >= 0 && arry[j] > arry[j + 1]; j--);//注意此處 j >= 0 判斷條件在前
if (j < 0) return;//結束
for (k = len - 1; k > j&&arry[k] < arry[j]; k--);
swap(arry[k], arry[j]);
for (int l = j + 1, r = len - 1; l < r; l++, r--)
swap(arry[l], arry[r]);
}
}
int main()
{
Permutation();
return 0;
}不知道大家是否記得STL---《algorithm》中的兩個函式next_permutation和prev_permutation。連結分別是next_permutation,prev_permutation。
next_permutation:對於當前的排列,如果在字典序中還存在下一個排列,返回真,並且將下一個排列賦予當前排列,如果不存在,就把當前排列進行遞增排序。
prev_permutation對於當前的排列,如果在字典序中還存在前一個排列,返回真,並且將前一個排列賦予當前排列,如果不存在,就把當前排列進行遞減排序。
那麼利用next_permutation可以很輕鬆的實現全排列。
程式碼如下:
#include<iostream>
#include<algorithm>
using namespace std;
int arry[3] = { 1,2,3 };//len==3;
void Permutation()
{
do
printf("%d%d%d\n", arry[0], arry[1], arry[2]);
while (next_permutation(arry, arry + 3));
}
int main()
{
Permutation();
return 0;
}三:改進
上面我們講了兩種方法來求解全排列,但是上面的問題是不可重複全排列,給出的初始序列各個元素互不相同,但是如果其中有相同的呢?結果會是如何?這個問題就是可重複全排列了。
我們知道對於一個n個元素的序列(分別是n1,n2,n3,,,,nn),如果其中有k個元素相等,那麼這個序列的全排列個數就是 n!/k!。這是數學內容了,不做細講。
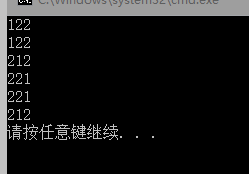
假如給出序列{1,2,2},用上述的遞迴和字典樹法求全排列:
對於遞迴:
明顯不對,有多個重複的排列。如何解決?
其實只要在交換元素之前判斷是否相等即可,改進程式碼如下:
#include<iostream>
#include<algorithm>
using namespace std;
int arry[3] = { 1,2,2 };
bool IsEqual(int s, int t)
{
for (int i = s; i < t; i++)
if (arry[i] == arry[t])
return true;
return false;
}
void Recursion(int s, int t)
{
if (s == t)
for_each(arry, arry + 3, [](int i) {printf("%d", i); }), printf("\n");
else
{
for (int i = s; i <= t; i++)
{
if (!IsEqual(s, i))//不相等才能交換
{
swap(arry[i], arry[s]);
Recursion(s + 1, t);
swap(arry[i], arry[s]);
}
}
}
}
int main()
{
Recursion(0, 2);
return 0;
}輸出如下:
為什麼那樣判斷?舉個例子:對於 1abc2xyz2 這樣的排列,我們交換1與第一個2,變成2abc1xyz2,按照遞迴的順序,接下來對abc1xyz2進行全排列;但是1是不能和第二個2交換的,如果交換了,變成了2abc2xyz1,按照遞迴的順序,接下來對abc2xyz1進行全排列,那麼問題來了,注意我紅色突出的兩個地方,這兩個全排列進行的都是同樣的工作,也就是如果1和第二個2交換必然會和前面重複。
同樣的對於字典序法,改進如下:
#include<iostream>
#include<algorithm>
using namespace std;
int arry[3] = { 1,2,2 };//len==3;
void Permutation()
{
int len = 3;
int j, k;
while (true)
{
printf("%d%d%d\n", arry[0], arry[1], arry[2]);
for (j = len - 2; j >= 0 && arry[j] >= arry[j + 1]; j--);//注意此處 j >= 0 判斷條件在前,加個等號即可
if (j < 0) return;//結束
for (k = len - 1; k > j&&arry[k] <= arry[j]; k--);//加個等號即可
swap(arry[k], arry[j]);
for (int l = j + 1, r = len - 1; l < r; l++, r--)
swap(arry[l], arry[r]);
}
}
int main()
{
Permutation();
return 0;
}對於STL中的next_permutation呢?這就不需多慮了,STL裡已經把相同元素的情況考慮進去了,程式碼不變。讀者可以自己試試。