評價方法大體可分為兩類,其主要區別在確定權重的方法上。一類是主觀賦權法,多數採取綜合諮詢評分確定權重,如綜合指數法,模糊綜合評價法,層次分析法,功效係數法等.另一類是客觀賦權,根據各指標間相關關係或各指標變異程度來確定權數,如主成分分析法,因子分析法,TOPSIS法等.
下面以2010年數學建模B題為例

基於主成分分析法的評價步驟如下:




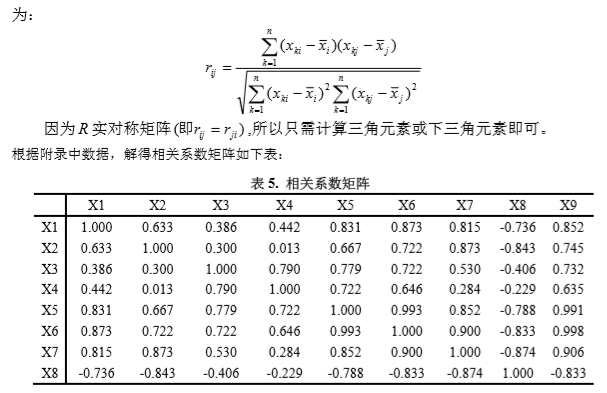
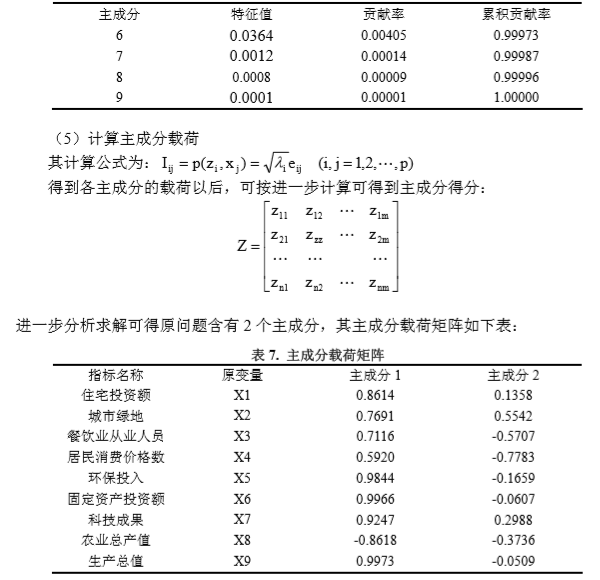
matlab求解:

clc;clear; 
da=... 
    [443.9  12601 25.91   250.9 141.91  1869.67  1102 220.9  4771.17 
    466.71  14771
 
 26.95   250.9 152.93  1994.73  1338 236.5  5210.12 
    584.51  18758 27.15   252.2 162.39  2187.06  1418 243.6   5741.03 
    694.3  24426 27.02   252.5 191.53  2452.11  1508 246.3  6694.23 
    922.61  26689 25.04   257.8 225.37  3084.66  1629 229.6  8087.83 
    936.36  28865 26.32   260.3 281.18  3542.55
 
  1701 205.5   9247.66 
    854.15  30609 29.02   263.4 310.85  3925.09  1953 206.9  10572.24 
    853.13  31795 28.96   271.7 366.12  4458.61  2396 210    12494.01 
    871.5  34256 30.12   287.4 422.37  4829.45  1866 210.2   14069.87 
    922.8  116929 30.17   286.3 460.42  5273.33  2166 209.1   15046.45 
    1136  351232
 
 28.43   254.5 484.5  6116     3408 153.5  18151.35]; 
%%%標準化矩陣 
cwsum=sum(da,1);       
[a,b]=size(da);   
for i=1:a     
    for j=1:b         
        vector1(i,j)= da(i,j)/cwsum(j);   %化為標準化矩陣     
    end
end %%%相關係數矩陣 
fprintf('相關係數矩陣：\n') 
std=corrcoef(da)      %計算相關係數矩陣 
[vec,val]=eig(std);   %求特徵值(val)及特徵向量(vec) 
newval=diag(val) ;    
[y,i]=sort(newval) ;   %對特徵根進行排序，y 為排序結果，i 為索引 
fprintf('特徵根排序：\n')
for   z=1:length(y)     
    newy(z)=y(length(y)+1-z); 
end
fprintf('%g\n',newy)  %%%顯示特徵根
rate=y/sum(y); 
fprintf('貢獻率：\n') 
newrate=newy/sum(newy) 
sumrate=0; 
newi=[]; 
for k=length(y):-1:1     
    sumrate=sumrate+rate(k);     
    newi(length(y)+1-k)=i(k);     
    if sumrate>0.85 
        break;     
    end
end       %記下累積貢獻率大 85%的特徵值的序號放入 newi 中 
fprintf('主成分數：%g\n\n',length(newi)); 
for p=1:length(newi)     
    for q=1:length(y)      
        vector2(q,p)=sqrt(newval(newi(p)))*vec(q,newi(p));%%%主成分載荷     
    end
end
fprintf('顯示載荷:\n'); 
disp(vector2); %顯示載荷 %%%求各主成分得分 
sco=vector1*vector2; 
csum=sum(sco,2); 
[newcsum,i]=sort(-1*csum); 
[newi,j]=sort(i); 
fprintf('計算得分：\n') %得分矩陣：sco 為各主成分得分；csum 為綜合得分；j 為排序結果 
score=[sco,csum,j]