線段樹+掃描線(有關掃描線的理解)
掃描線:
下面是來自soar轉載的一篇部落格。
這篇部落格解決了我對算區間長度時的不理解。實際上這個線段樹的葉子節點儲存的是這個點x座標到下一個x座標(排序後的)的區間長度。
題意:
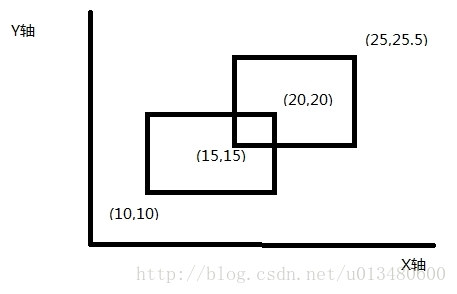
二維平面有n個平行於座標軸的矩形,現在要求出這些矩形的總面積. 重疊部分只能算一次.
分析:
線段樹的典型掃描線用法.
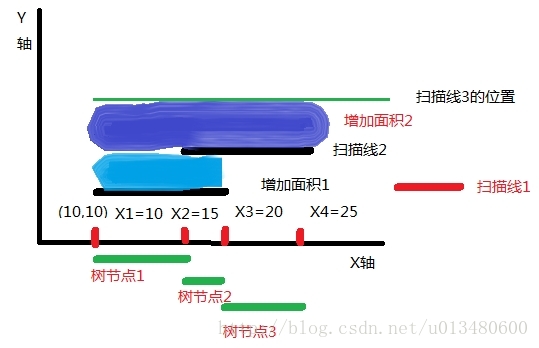
首先假設有下圖兩個矩陣,我們如果用掃描線的方法如何計算它們的總面積呢?
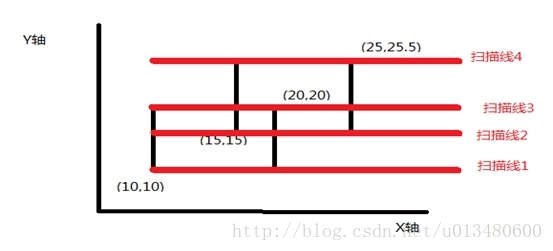
首先我們將矩形的上下邊分為上位邊(即y座標大的那條平行於x軸的邊),和下位邊(y座標小的平行於x軸的邊).然後我們把所有矩形的上下位邊按照他們y座標從小到大排序,可以得到4條掃描線:
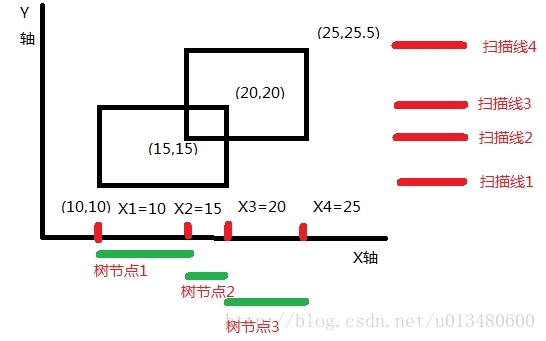
又因為上面2個矩形有4個不同的浮點數x座標,所以我們需要把x座標離散化,這樣才能用線段樹來維護資訊.所以我們這樣離散化:
由上圖可知,4個不同的x座標把x軸分成了3段有效的區間.這裡要注意我們線段樹中每個葉節點(控制區間[L,L])不是指X[L]座標,而是指區間[X[L],X[L+1]].線段樹中其他節點控制的區間[L,R],也是指的x座標軸的第L個區間到第R個區間的範圍,也就是X[L]到X[R+1]座標的範圍.
然後我們Y座標從小到大的順序讀入每條掃描線,並維護當前我們所讀入的所有掃描線能有效覆蓋X軸的最大長度sum[1].這裡特別要注意如果我們讀入的掃描線是矩形的下位邊,那麼我們就使得該範圍的標記cnt位+1,如果是上位邊,那麼該範圍的cnt就-1.所以如果cnt=0時,表示該節點控制的範圍沒有被覆蓋,只要cnt!=0 就表示該節點控制的幾塊區間仍然被覆蓋.
下面依次讀入每條矩陣邊,來一一分析,首先是讀入第一條矩陣邊:
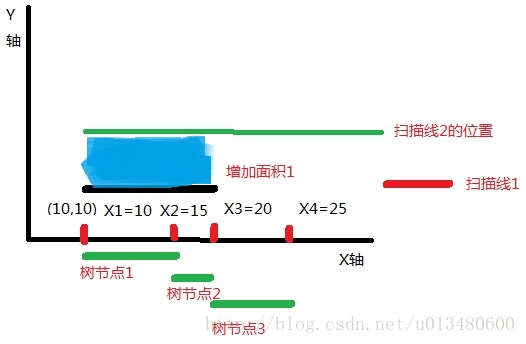
我們讀入了矩形1的下位邊,那麼該區域的cnt就+1=1了,所以該區域[10,20]就被覆蓋了,然後可以推出整個區域被覆蓋的長度是10.再根據第二條掃描線離第一條掃描線的高度差為5.所以不管你第二條掃描線是哪個矩形的什麼邊,或者能覆蓋到X軸的什麼範圍,我上圖中藍色的矩形面積肯定是要算到總面積裡面去的.即總面積ret+=sum[1]*(掃描線2的高度-掃描線1的高度). (想想看是不是這樣).
下面讀第二條掃描線:
由於第二條掃描線也是下位邊,所以[15,20]和[20,25]的cnt+1.使得我們覆蓋的範圍變成了[10,25]了,並且第3條掃描線在20高度,所以這次我們必然增加的面積是上面深藍色的長條=sum[1]*(掃描線3的高度-掃描線2的高度).
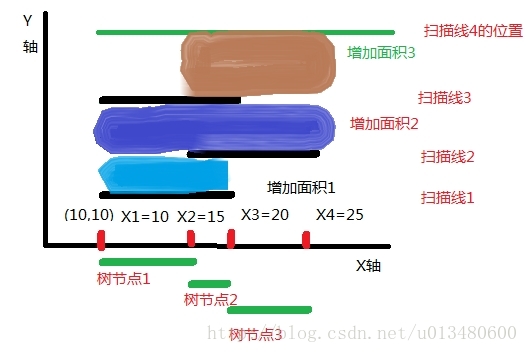
下面我們要讀第三條掃描線了:
由於第三條掃描線是區間[10,20]的上位邊,所以對應區間的cnt要-1,所以使得區間[10,15]的cnt=0了,而[15,20]區間的cnt-1之後變成了1.[20,25]的cnt仍然為1,不變.所以當前覆蓋的有效x軸長度為10,即區間[15,25].所以增加的面積是圖中褐色的部分.
到此,矩形的面積和就算出來了.由於對於任一矩形都是先讀下位邊(cnt+1),再讀上位邊(cnt-1)的,所以在更新線段樹的過程中,任意節點的cnt都是>=0的.
下面說程式碼實現部分:
首先建立一個node結構體用來儲存每條掃描線,node中有資訊:
l: 表示掃描線的左端x座標
r:表示掃描線的右端x座標
h: 表示掃描線的高度
d: 為1或-1,標記掃描線是矩形的上位還是下位邊.
我們首先讀入所有矩形的資訊,每讀入一個矩形資訊我們就更新兩條掃描線,並且把矩形的兩個端點x座標放入X[MAXN]陣列中,
然後我們對node和X都排序,node按h值從小到大排序.
X按從小到大排序.
然後我們在X的本地陣列內,對X去重,並且用k表示一共有多少個X.
當我們需要找到第i個區域的兩端點座標時,只需要X[i]和X]i+1].
線段樹維護cnt(根本資訊)和sum兩個資訊,其中sum為double,cnt為int型.
cnt: >=0時表示本節點控制的區域內下位邊個數-上位邊個數的結果.如果==-1時,表示本節點左右子樹的上下位邊數不一致.
sum: 本節點控制的區域內cnt值不為0的區域總長度.
線段樹操作:
PushDown(i,l,r):如果cnt!=-1,那麼下放cnt資訊,並更新子節點的sum資訊.
PushUp(i,l,r): 根據子節點的cnt值和sum值更新父節點的cnt和sum值.
update(ql,qr,v,i,l,r): 使得[ql,qr]與[l,r]區間的公共部分cnt值+v.
如果ql<=l && r<=qr 且 cnt[i]!=-1的話,直接更新並return
否則先PushDown
在一次遞迴更新左右兒子
最後PushUp.
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<queue>
#include<algorithm>
#include<map>
#include<iomanip>
#define INF 99999999
using namespace std;
const int MAX=200+10;
int mark[MAX<<2];//記錄某個區間的下底邊個數
double sum[MAX<<2];//記錄某個區間的下底邊總長度
double hash[MAX];//對x進行離散化,否則x為浮點數且很大無法進行線段樹
//以橫座標作為線段(區間),對橫座標線段進行掃描
//掃描的作用是每次更新下底邊總長度和下底邊個數,增加新面積
struct seg{//線段
double l,r,h;
int d;
seg(){}
seg(double x1,double x2,double H,int c):l(x1),r(x2),h(H),d(c){}
bool operator<(const seg &a)const{
return h<a.h;
}
}s[MAX];
void Upfather(int n,int left,int right){
if(mark[n])sum[n]=hash[right+1]-hash[left];//表示該區間整個線段長度可以作為底邊
else if(left == right)sum[n]=0;//葉子結點則底邊長度為0(區間內線段長度為0)
else sum[n]=sum[n<<1]+sum[n<<1|1];
}
void Update(int L,int R,int d,int n,int left,int right){
if(L<=left && right<=R){//該區間是當前掃描線段的一部分,則該區間下底邊總長以及上下底邊個數差更新
mark[n]+=d;//更新底邊相差差個數
Upfather(n,left,right);//更新底邊長
return;
}
int mid=left+right>>1;
if(L<=mid)Update(L,R,d,n<<1,left,mid);
if(R>mid)Update(L,R,d,n<<1|1,mid+1,right);
Upfather(n,left,right);
}
int search(double key,double* x,int n){
int left=0,right=n-1;
while(left<=right){
int mid=left+right>>1;
if(x[mid] == key)return mid;
if(x[mid]>key)right=mid-1;
else left=mid+1;
}
return -1;
}
int main(){
int n,num=0;
double x1,x2,y1,y2;
while(cin>>n,n){
int k=0;
for(int i=0;i<n;++i){
cin>>x1>>y1>>x2>>y2;
hash[k]=x1;
s[k++]=seg(x1,x2,y1,1);
hash[k]=x2;
s[k++]=seg(x1,x2,y2,-1);
}
sort(hash,hash+k);
sort(s,s+k);
int m=1;
for(int i=1;i<k;++i)//去重複端點
if(hash[i] != hash[i-1])hash[m++]=hash[i];
double ans=0;
//memset(mark,0,sizeof mark);
//memset(sum,0,sizeof sum);如果下面是i<k-1則要初始化,因為如果對第k-1條線段掃描時會使得mark,sum為0才不用初始化的
for(int i=0;i<k;++i){//掃描線段
int L=search(s[i].l,hash,m);
int R=search(s[i].r,hash,m)-1;
Update(L,R,s[i].d,1,0,m-1);//掃描線段時更新底邊長度和底邊相差個數
ans+=sum[1]*(s[i+1].h-s[i].h);//新增加面積
}
printf("Test case #%d\nTotal explored area: %.2lf\n\n",++num,ans);
}
return 0;
}
/*
這裡注意下掃描線段時r-1:int R=search(s[i].l,hash,m)-1;
計算底邊長時r+1:if(mark[n])sum[n]=hash[right+1]-hash[left];
解釋:假設現在有一個線段左端點是l=0,右端點是r=m-1
則我們去更新的時候,會算到sum[1]=hash[mid]-hash[left]+hash[right]-hash[mid+1]
這樣的到的底邊長sum是錯誤的,why?因為少算了mid~mid+1的距離,由於我們這利用了
離散化且區間表示線段,所以mid~mid+1之間是有長度的,比如hash[3]=1.2,hash[4]=5.6,mid=3
所以這裡用r-1,r+1就很好理解了
*/ 無註釋精簡版:
#include<bits/stdc++.h>
using namespace std;
#define lson i<<1,l,m
#define rson i<<1|1,m+1,r
const int maxn=222;
double x[maxn];
struct node
{
double l,r,h;//左右座標,高度
int d;//標記上位邊還是下位邊
node() {}
node(double l,double r,double h,int d):l(l),r(r),h(h),d(d) {}
bool operator < (const node &a)const
{
return h<a.h;
}
} line[maxn];
int cnt[maxn<<2];
double sum[maxn<<2];
void pushup(int i,int l,int r)
{
if(cnt[i])
{
sum[i]=x[r+1]-x[l];
}
else
{
sum[i]=sum[i<<1]+sum[i<<1|1];
}
}
void update(int ql,int qr,int v,int i,int l,int r)
{
if(ql<=l && qr>=r)
{
cnt[i]+=v;
pushup(i,l,r);
return ;
}
int m=(l+r)>>1;
if(ql<=m)update(ql,qr,v,lson);
if(qr>m)update(ql,qr,v,rson);
pushup(i,l,r);
}
int main()
{
int q;
int kase=0;
while(cin>>q&&q)
{
memset(cnt,0,sizeof(cnt));//相當於build
memset(sum,0,sizeof(sum));//相當於build
int n=0,m=0;
for(int i=1; i<=q; i++)
{
double x1,y1,x2,y2;
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
x[++n]=x1;
x[++n]=x2;
line[++m]=node(x1,x2,y1,1);
line[++m]=node(x1,x2,y2,-1);
}
sort(x+1,x+1+n);
sort(line+1,line+1+m);
int k=1;
/* for(int i=2;i<=n;i++)//去重
{
if(x[i]!=x[i-1])x[++k]=x[i];
}*/
k=unique(x+1,x+n+1)-x-1;//直接用STL中的unique函式。
double ans=0.0;
for(int i=1; i<m; i++)
{
int l=lower_bound(x+1,x+k+1,line[i].l)-x;
int r=lower_bound(x+1,x+k+1,line[i].r)-x;
r--;
if(l<=r)update(l,r,line[i].d,1,1,k-1);
ans+=sum[1]*(line[i+1].h-line[i].h);
}
printf("Test case #%d\nTotal explored area: %.2f\n\n",++kase,ans);
}
}