剛學習了計算機圖形學這門課程，為奠定根基的演算法所傾倒，特此記錄一二。

• 區域填充是指從區域內的某一個象素點（種子點）開始，由內向外將填充色擴充套件到整個區域內的過程。
• 區域是指已經表示成點陣形式的填充圖形，它是相互連通的一組畫素的集合。（前面描述的 X - 掃描線演算法適用於頂點表達的多邊形）
• 區域填充演算法（邊界填充演算法和泛填充演算法）是根據區域內的一個已知象素點（種子點）出發，找到區域內其他象素點的過程，所以把這一類演算法也成為種子填充演算法。

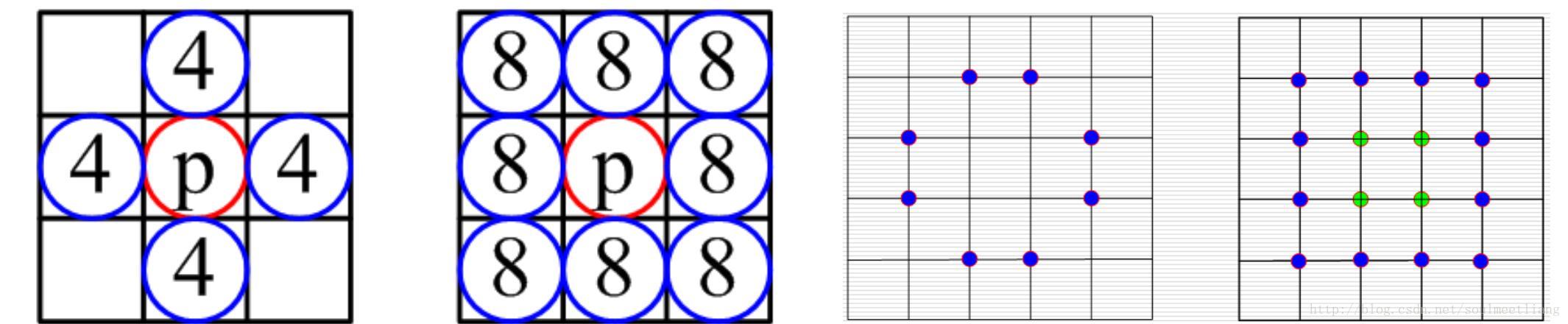
邊界填充演算法—4 - 連通區域與 8 - 連通區域

• 4-連通區域：從區域上的一點出發，通過訪問已知點的4-鄰接點，在不越出區域的前提下，遍歷區域內的所有象素點。
• 8-連通區域：從區域上的一點出發，通過訪問已知點的8-鄰接點，在不越出區域的前提下，遍歷區域內的所有象素點。
  

邊界填充演算法

• 演算法的輸入：種子點座標(x,y)，填充色以及邊界顏色。
• 利用堆疊實現簡單的種子填充演算法：
  演算法從種子點開始檢測相鄰位置是否是邊界顏色，若不是就用填充色著色，並檢測該畫素點的相鄰位置，直到檢測完區域邊界顏色範圍內的所有畫素為止。

演算法步驟

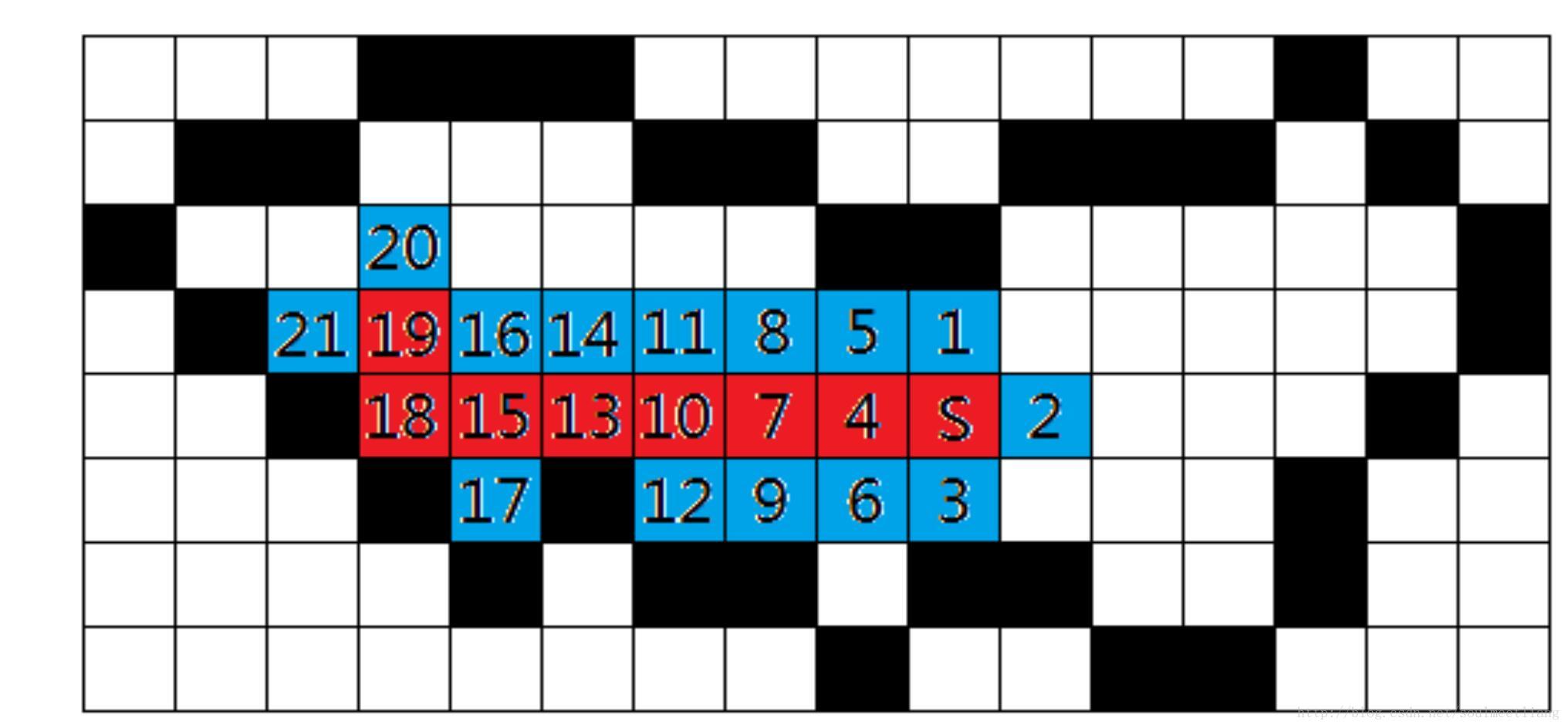
• 棧結構實現4-(8-)連通邊界填充演算法的演算法步驟為：
  種子象素入棧；當棧非空時重複執行如下三步操作：
  
  • (a) 棧頂象素出棧；
  • (b) 將出棧象素置成填充色；
  • (c) 檢查出棧象素的4-(8-)鄰接點，若其中某個象素點不是邊界色且未置成多邊形色，則把該象素入棧。

圖示

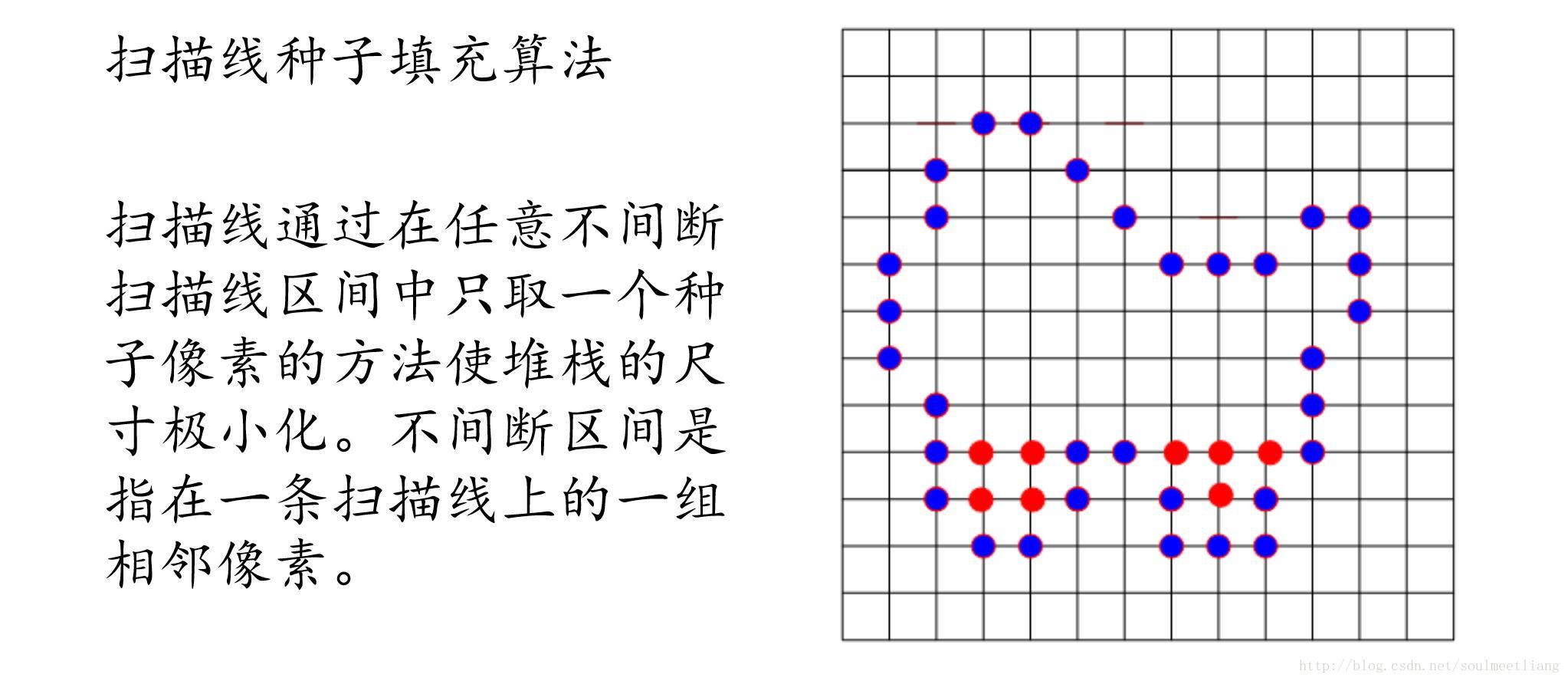
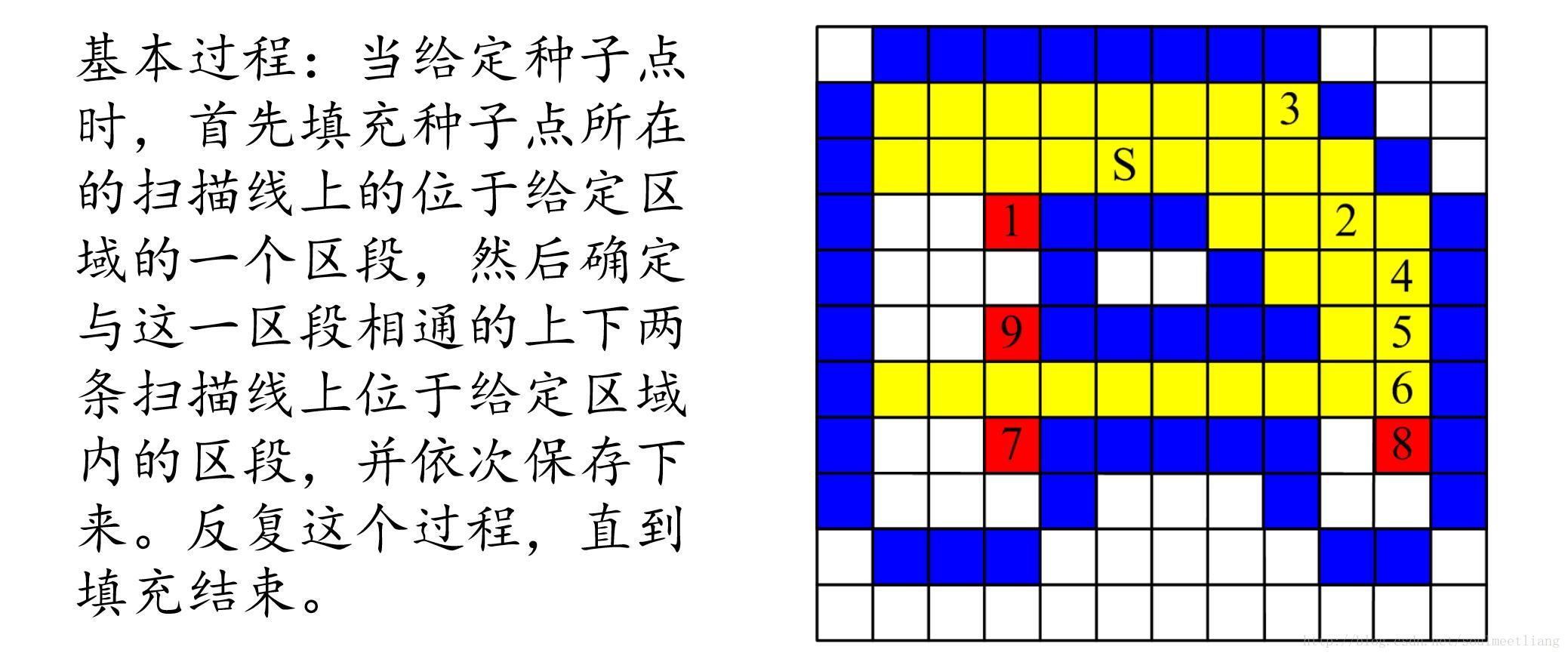
掃描線種子填充演算法

內外測試

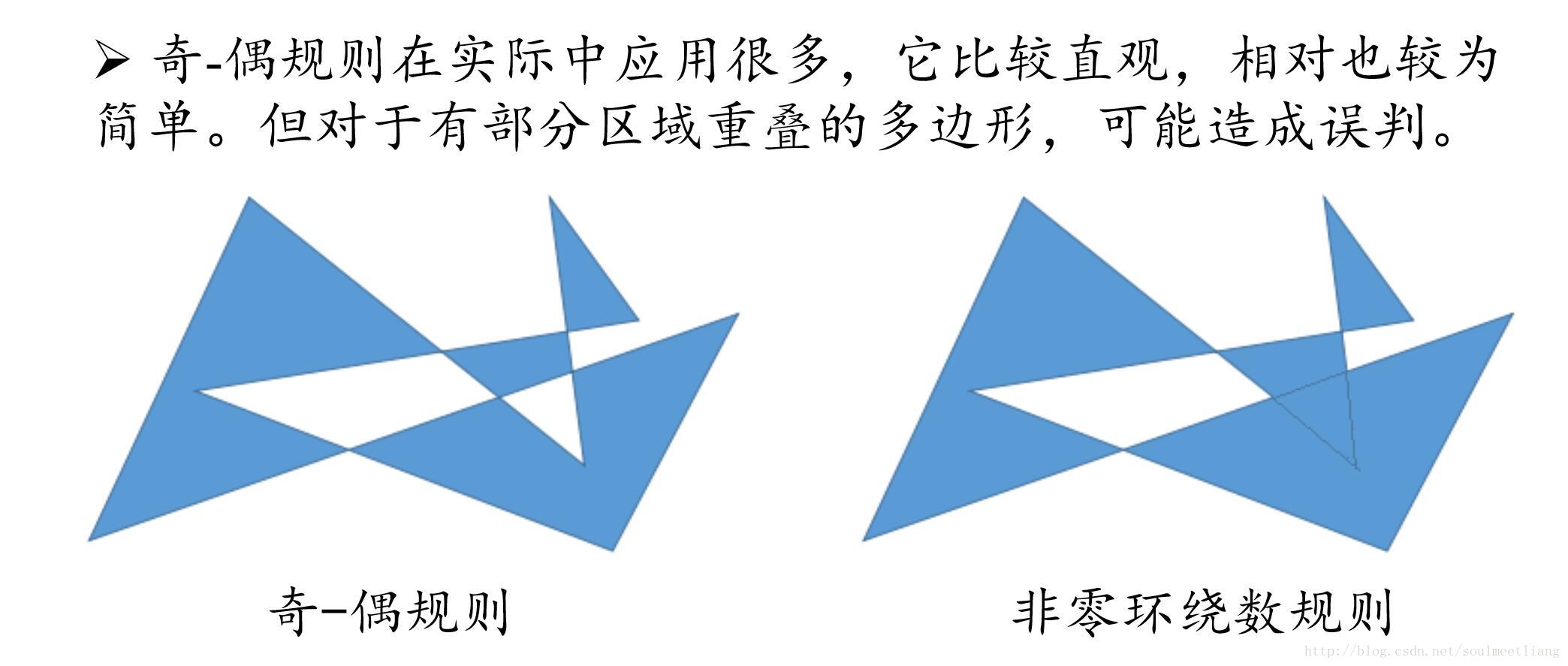
奇-偶規則

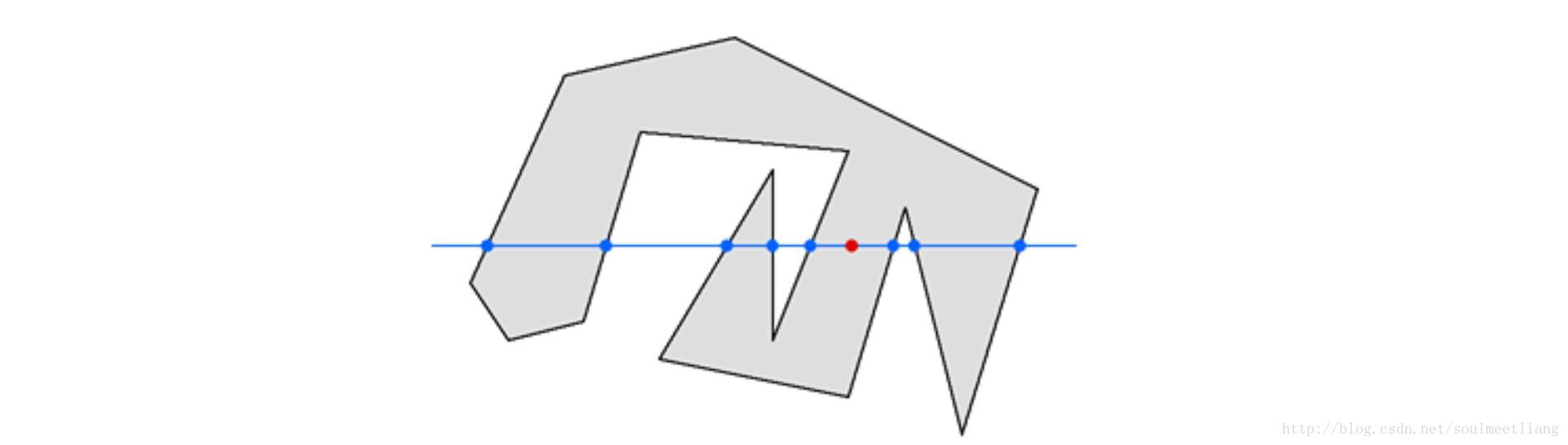
• 奇-偶規則（Odd-even Rule）
  從任意位置p作一條射線，若與該射線相交的多邊形邊的數目為奇數，則p是多邊形內部點，否則是外部點。

非零環繞數規則

非零環繞數規則（Nonzero Winding Number Rule）

• 首先使多邊形的邊變為向量。
• 將環繞數初始化為零。
• 再從任意位置p作一條射線。當從p點沿射線方向移動時，對在每個方向上穿過射線的邊計數，每當多邊形的邊從右到左穿過射線時，環繞數加1，從左到右時，環繞數減1。
• 處理完多邊形的所有相關邊之後，若環繞數為非零，則p為內部點，否則，p是外部點。

兩種規則的比較