[圖形學] 經典演算法 - Kajiya三維紋理渲染毛髮
簡介
渲染複雜度高細節豐富的場景一直是影象繪製的重要目標。一個想法是引入不同尺度的層次,每一層次對應一種精度幾何模型。因此那些複雜的小物體可以被歸類為可被簡化的幾何物體。
但是,繪製毛皮表面依然面臨著一個重大的問題,傳統的方法會產生一個嚴重的走樣問題。我們認為這是幾何物體的尺度定義不正確導致的。還有一種方法是把精細的幾何物體作為紋理而不是幾何物體來看待。我們在此將討論這種方法。
本文描述了一種新型的紋理對映,稱作texel,它是按照體積密度來計算的。texel是一個三維的紋理對映,包含法線、切線和次法線。光照模型的引數根據體積自由分佈。一個texel和特定表面的幾何形狀沒有關聯。實際上,它的目的是包含在特定體積中的高複雜度的曲面集合,由於texel的渲染時間和幾何表面的複雜度無關。事實上,使用texel後,我們可以摒棄通常的幾何模型表面概念。也就是說,我們可以直接渲染texel,它能用於任意定義的表面幾何體。
我們將使用texel的概念來描述毛皮表面,並提出一種渲染這類表面的演算法。
高精度物體渲染概述
針對高精度的模型場景的渲染,已經有了不少嘗試的解決方案。一種方法是使用暴力運算來解決這一問題,比較早的工作是由Csuri做出的,它用大量多邊形生成了煙和毛髮的影象。最近,Weil使用上千個lambert圓柱渲染布料。不幸的是,在較大尺度下,微觀幾何表面會引起嚴重的走樣現象,它們無法通過傳統的反走樣演算法來消除。這些影象看起來會比較破碎,也就是說,對於頭髮而言,看起來會像刺。
暴力演算法是失敗的,因為我們應該通過紋理和光照模型來繪製我們所需要的細節,而非幾何體的堆疊。我們可以利用像畫家使用的視錯覺來表現,來暗示場景中的細節遠遠超過了影象的解析度。當一個人走得更近來觀察畫作時,畫家的伎倆就會被識破 —— 此時繪畫中細緻的物體,只呈現出無意義的色彩斑點。
最為成功的渲染高複雜度場景的嘗試是基於粒子系統的。我們相信他們的成功是因為粒子系統體現了無幾何圖形繪製的思想。沿著粒子系統的思路,我們使用光照模型和紋理來直接渲染畫素,而不通過細節的幾何體。從某種意義上來說,本文將粒子系統推廣到了光線追蹤。正如讀者很容易看到的,雖然我們的渲染演算法是非常不同的,但粒子系統和texel是互補的,例如,可以使用粒子系統產生texel模型。事實上,本篇文章經過修改後,可以獨立於粒子的數量進行粒子系統的渲染。
Miller提出了一種幾何和光照模型結合的辦法,同樣出於本文中繪製毛絨動物的目的。但是,和粒子系統一樣,演算法的幾何體複雜度取決於頭髮的數量。texel的概念來自於Blinn渲染體積密度的思想。Bllin描述了一種繪製大量均勻分佈在平面內的微觀球形顆粒來描述外觀,以生成雲、塵土以及土星的光環。因為Blinn對大氣定向運動感興趣,他分析整合了它的方程得到了一個簡單的光照模型。
對於Kajiya和Von Herren而言,Blinn的方程是為了通過直接計算來求解各向異性材質,它本質上是光線追蹤的體積繪製技術。由於我們的工作基於他們的早期成果,現在我們將簡要地討論一下Kajiya和Von Herzen的方程。
當一束光穿過球形粒子時,它會發生散射和衰減。衰減主要取決於光線體積的區域性密度,而散射依賴於例子散射光的密度和每個粒子的反照率。由於粒子在某些方向上會部分遮擋散射,散射的數量在不同方向上發生變化。這種散射作用然後被其它粒子衰減以及重新散射。
這一模型忽略了散射粒子周圍的衍射。
在光線追蹤中,我們跟隨來自眼睛的光線向後朝向光源的位置。由於粒子遮擋引起的沿光線逐漸衰減是根據從眼睛發出的射線上的每個點來計算的。在光線穿過粒子體積的每個點,我們計算向眼睛方向散射的光的量,然後將所有值加起來得到達到眼睛的總光量。在這項技術中,我們使用Blinn方程的反照率和單散射來近似。也就是說,我們假設來自多重散射的貢獻是可以忽略不計的,並假設光從光源到眼睛只散射一次。這個假設對於低反照率粒子而言準確性較好,並且會隨著反照率的增加而受到影響。

圖1顯示了該情況的示意圖。上圖是一個包含了粒子的體積,它被一條射線穿過,線上每個點的密度為P(x,y,z)。到達眼睛的光線沿著R進行計算。對於距離t上的點P = (x(t), y(t),z(t)),每個光源光照l(i)乘以相位因子p(cos theta)的結果反映了有多少光從光源散射到光線中。然後,這個點上的亮度還會經過粒子密度p的加權運算。由介質引起的點P和A之間的衰減可由射線上粒子密度的積分得到,方程為:

方程1計算了密度p的透明度T,沿著每個單位距離ds的密度累積乘以透射係數![]() 。係數
。係數![]() 將粒子的密度轉換為衰減係數。值tfar和tnear是參與運算的密度的遠近距離。
將粒子的密度轉換為衰減係數。值tfar和tnear是參與運算的密度的遠近距離。
方程2根據三個因子對沿射線(x(t),y(t),z(t))的每個dt的亮度進行積分來計算亮度B。第一個因子將介質中的光線衰減到表面,粒子密度體積裡深埋了許多被其它粒子隱藏的明亮粒子,因此累積的透射係數低,並且對於最終的畫素,粒子並不會貢獻太多的光。請注意,這個係數是根據等式1來計算的。第二個因子將到達粒子的每個光源的光強l(i)(如等式1那樣作為透射率給出)乘以每個粒子的照明模型,這由相位因子p(cos theta)給出。這個相位因子是光和眼睛之間的夾角的函式,它代表了散射光的遮擋量,就像月相一樣。第三個因子根據給定點的粒子密度來加權亮度。少量明亮的粒子貢獻的光比大量暗淡粒子要少。
有多種方式計算光照分量I(i)。Blinn假設材質是各向同性的,並計算每個光源從點P到C的介質透明度。 Kajiya 和 Von Herzen則認為光源在無限遠的距離,併為沿著一個平行的波陣面預計算體積中每個點的強度。Rushmeier和Torrance求解一個Ii域上的線性方程。
繼Blinn之後,很多人對體積密度這一領域進行了擴充套件:Voss(1983), Max(1983), Kajiya and Von Herzen(1984),
Max(1986b, 1986e), Rushmeier and Torrance(1987), 以及 Nishita,Miyawaki and Nakamae(1987)。他們的演算法都是在Blinn的原始工作上進行擴充套件,用於繪製非均勻分佈密度的物體,考慮高反照率粒子的解決方案,以及更一般的幾何形狀。Rushmeier and Torrance(1987)的工作是至今為止最為複雜的:它計算了多次散射後光的物理精確分佈——儘管使用的是各向同性散射的模型。
近年來,科學視覺化的普及帶動了大量在體積渲染上的研究。例如 Sabella(1988), Upson and Keeler (1988), Drebin, Carpenter, 以及 Hanrahan(1988)。本文介紹的技術可以直接用於向量場的體積繪製。特別地,這項工作的一個結果和體積渲染有所關聯,即陰影的重要性。在結果的小節中,我們渲染了一個沒有陰影的相同紋理。如圖11,12所示,在不考慮陰影的情況下進行渲染會造成一種不切實際的情況,導致我們的視覺系統不能很好地解釋這一畫面。
我們還指出,本文提出的技術非常適合光線追蹤/分散式光線追蹤/渲染方程的框架。也就是說,texels可以和光線追蹤可控的各種各樣的基元(primitive)進行混合。我們尚不清楚texel是否和影象渲染的光照相容。
Texels
Kajiya and Von Herzeu(1984) 提出,體積密度可能能夠呈現除了塵埃、煙塵顆粒之外的許多複雜物體:將包含諸如毛髮和毛絨表面等現象。我們開始嘗試推廣這項工作。在研究過程中,我們發現使用體積密度來模擬表面的想法並不完全合適。雖然在積極密度內使用照明模型而非球形粒子的思路是正確的,但是我們已經發現,不能簡單地用表面照明模型來代替粒子照明模型,因為表面散射的物理過程和粒子散射的物理過程有著很大不同,因此必須推匯出控制渲染過程的新方程。
為了推廣體積密度,我們現在介紹texels。在實際應用中,texel是一個三維陣列,引數與一組微觀表面的視覺特性近似。如果用texels來代替幾何圖形,比如山上的樹木,那麼像樹葉樹枝這樣的微觀表面將儲存到體積陣列中。在空間中的每個點,都儲存了多項資料。首先是微觀表面的密度,在某些點上,空間是空的;在另一些點上,有葉子密集的陣列。第二項是整個空間的光照模型。在texel中,每個葉子不再儲存為多邊形,而是用散射函式來代表葉子的集合,散射函式模擬了光是如何從體積單元包含的表面集合中散射的。這個散射函式是由一對資料來表示的,第一個是組織,它代表了每個單位微觀表面的主要朝向,其次是反射率函式。
texels可由多種方式產生。對於很多有趣的情況,我們還沒有研究過產生texel的方式。例如,可以使用某種三維掃描轉換技術,將樹的幾何結構取樣成三維陣列。然而,我們還沒有完成這項工作。為了表現毛皮,texel的生成是比較簡單的,我們將在這一節中給出。
texel用於模擬包含了不少表面的體積單元,而非球形粒子。因此texel的第一個分量是標量密度p,他不表示相對體積,而是表示包含在體積單元內微觀表面的相對投影面積的近似值。texel的第二個分量是體積單元中微觀表面的區域性朝向B。第三個分量是光照模型部分,它決定了光是如何從表面散射的。
定義。texel是一個三元組![]() ,即一個標量密度
,即一個標量密度![]() ,一組向量
,一組向量![]() ,以及一個光反射函式
,以及一個光反射函式![]()
標量密度p描述了微觀表面覆蓋的體積單元的投影單位面積。它本應是考慮到視線的張量,但是我們採用了近似法,所以將其設計為各向同性的標量。
向量組B描述了texel裡表面的區域性方向。它是一個座標系的基底N-T-B,也就是法線,切線和次法線。
雙向反射方程描述了其中包含的表面型別。我們可以將![]() 和B組合到單個各向異性照明模型場中,但是我們在這裡將它們分開了,這是因為其中一個分量在整個體積中是常數時,另一分量會變化。
和B組合到單個各向異性照明模型場中,但是我們在這裡將它們分開了,這是因為其中一個分量在整個體積中是常數時,另一分量會變化。
texels是體積密度的一種自然的擴充套件。因為在體積密度中,球體是基於物理以及各向同性的,所以反射場是均勻的。因此,它們不需要分佈在整個密度中,而是可以被建模為單個量。texel就能很好地描述這一點。
渲染texels
如何修改體積密度來模擬頭髮?一種樸素的方法是僅僅重新定義密度p,來反射每個體積處的頭髮密度。計算對應於圓柱而非球體的散射光照模型。不幸的是,這種直接的方法雖然在某種程度上是對的,但也有缺點。
為了深入理解為什麼體積密度不適合渲染微觀物體,我們考慮通過體積密度渲染單個平面表面。假設表面被儲存為體積密度,它平分了整個立方體(如圖2)。表面的光學深度很高,它模擬了一個不透明的表面。假設粒子照明模型的相位粒子是方程1和2中的lamber表面照明模型。現在我們不使用方程1,2來計算表面的透明度和亮度。
對於透明度計算,即使光學深度引數設定的很高,密度在指數的線性積分也會非常小,這是因為表面是無限薄的,所以線性積分只將在一個點上穿透表面,也就是0點處。
亮度計算也會出現同樣的問題。亮度積分函式產生一個有限的值,它對沿射線的積分貢獻為0,因為亮度積分函式只在單個點處為非零。
這個表面的透明度和亮度都將是0——這意味著一個看不見的表面。顯然,我們需要對體繪製進行一些修改,使其能夠繪製表面。問題在於微觀表面的相對體積並不像粒子密度那樣可以決定表面的亮度和不透明度,並且可以反射其入射光的100%,而它的相對體積將為0。因此,我們使用的所謂密度是由Dirac函式給出的,這一點再加上一個更通用的光照模型,就是texel概念的精髓。

texels以類似於體積密度推廣的形式呈現。同樣的,方程模擬了圖1所示的情況。texel包含了許多表面,表面上投影區域密度為P(x,y,z),每個點都被射線穿透。達到眼睛的光沿著射線R進行計算。在射線上距離為t的點P = (x(t),y(t),z(t)) 處,每個光源的光強L(i)乘以雙向反射函式![]() ,表示了從光源到射線散射了多少光。然後該點上的投影區域密度將對亮度進行加權。由介質引起的點P和A之間的衰減由射線的密度之和給出。
,表示了從光源到射線散射了多少光。然後該點上的投影區域密度將對亮度進行加權。由介質引起的點P和A之間的衰減由射線的密度之和給出。
texel光照的方程如下:

方程3,4和方程1,2非常類似。方程3和1的區別在於用求和取代了線性積分。我們使用總和,是因為可以整合Dirac函式在每個微觀表面上的貢獻。
方程4和方程2的關係也非常明顯,同樣是用求和取代了線性積分。第一項代表了圖1中沿著射線段AP的衰減,第二項模擬微觀表面上的散射。在方程1中有一項包含了每個光源,到達微觀表面的光照I(i)乘上微觀表面的雙向反射函式。最後,第三項,乘以投影區域密度來縮放反射光強度。
texels的投射方程3是一個總和而非積分。這個總和是在每個表面上沿著光線的密度進行的,如果這個和是無限的,那麼傳輸係數為0,表明密度是完全不透明的。亮度方程4也是一個總和而非積分,這是因為,在每一個和光線相交的表面上,我們都在該點上增加了表面的亮度貢獻。
等式4似乎總會得到一個無限的量,但請記住,總和的項在沒有表面的地方為0,而在任一表面之後,光學深度將很高,並且衰減所有貢獻到0。因此,這個和是有限的。
我們可以用方程1遞迴計算入射強度I的計算,也就是說,光線從點P射向每個光源i(如圖1)。方程1可以計算出透射係數。強度I(i)僅是光源沿著線段PC透射係數衰減的亮度。
如果通過加上沿著原始射線的每個點對應的項來評估總和,則剛剛描述的演算法的計算不會太耗時。在下一節提出的演算法將通過一種蒙特卡洛處理來近似這些和,根據光線跟蹤的思想來計算射線隨機取樣的期望值。
Texel渲染演算法
texel渲染演算法使用沿著射線的隨機樣本的期望值來近似,從而計算上述和。為了求得從給定光線向後發射的光的強度,我們計算光線和每個texel邊界的交點,然後沿著交點射線的距離形成了從t(near)到t(far)的間隔,如圖1中的A,D所示。為了能夠計算總和,我們使用稱為分層取樣的技術。我們把光線分成一個個片段(如圖1中繪製的那樣)。在每個區段中,隨機選擇點來計算散射項,例如點P。光照I(i)是遞迴地朝每個光源射出一條射線來計算的,正如前面討論的。最後計算段的總和,來近似方程3,4中的量。
1.將光線和所有的texel邊界求交,找到每一個texel的t(near)和t(far)。從前到後的位置排序所有交點,並和距離匹配。找到所有線段中最小值,使得Tnear = min[t(near)],同樣地,找到Tfar = max[t(far)]。
2. 將從Tnear到Tfar的射線分成多個長度為Li的線段Si,其中1/L是一個相對的長度,即使用使用者設定的世界座標中每單位距離的取樣數(最後一段可能比L要短)。
3.統一設定透明度。
4.對於每個線段:
4.1 從取樣點向每個光源發射陰影光線,來計算到達該點的光的總量。
4.2 根據光照模型和照明強度來計算亮度,並乘以透明度給出畫素的總體亮度貢獻:![]()
4.3 用![]() 乘以透明度,即線段的透射係數。
乘以透明度,即線段的透射係數。
5. 在末端的線段上,像前文所提一樣計算亮度,但是需要根據線段的分數長度進行歸一化。
在上述演算法中需要步驟5來避免蒙特卡洛計算中的偏差。如果末端線段被認為是完整長度的線段,那麼平均值將被丟棄,這會使得體積的邊緣看起來比表面稍暗。
這一章節討論了渲染單個texel的演算法。然而,為了繪製毛絨物體的影象,必須執行四個步驟。也就是texels的建立,texels到世界空間的對映,光線和texels求交,以及光照模型的計算。
為毛髮生成texels
我們現在討論生成毛髮片段texel的方法。一般的問題在於生成飄逸的長髮。可以使用粒子系統記錄三維陣列來跟蹤單個頭發的運動軌跡。粒子將會留下一個反走樣的密度軌跡,並和之前的密度相加。
可以通過僅在每個點儲存密度p和向量組B(法線/切線/次法線)來簡化毛髮的texel。因為雙向反射函式對於每個頭髮都是固定的,相同的(如果頭髮不變色的話)。因此,不必將其儲存在每個資料結構中。對於光照模型的推導,我們可以把一個人的頭髮看做一個無限薄的圓柱表面,因此,向量組B所需的唯一元素是沿著頭髮的切向向量,而其餘的部分,法線以及次法線,不會進入光照計算,因而被省略。因此,產生毛髮的粒子系統不僅會留下密度軌跡,還會儲存表示p的速度方向的切向量。
本文中給出的泰迪熊模型使用了一個單一texel在熊的面板上重複繪製。texel的內容是使用粒子系統方法的一個非常簡化的版本生成的。泰迪熊的所有毛髮都是直線,指向同一個方向,即垂直於頭皮的方向(在texel座標空間)。這意味著毛髮將沿著儲存texel的三維陣列的軸線。因此,切線向量都是相同的,因為它們都垂直於頭皮。因此,它們也被排除在體積結構之外。


熊的毛髮texel被儲存在一個40x40x10的數組裡。陣列的內容是基於以下原則設計的:
1. “毛髮”按照Possion disk來分佈。
2. Possion disk使用圓環拓撲進行建立,因此單個紋理可以在不顯示接縫的情況下覆蓋整個熊的表面。
3. 動物的皮毛通常有兩層,“外層”以及"內層"。內層使用短毛皮覆蓋,外層則是稀疏的長毛皮。我們發現這是一個避免毛髮看上去像刷出來的重要的特徵。
一個建模程式允許我們搜尋引數空間並向我們展示texel的頂部和側面投影。我們從審美角度(帶有隨意性),建立了圖15和16中的texel。
texels對映到世界空間
通過在熊的表面覆蓋texel,我們建立了一隻被毛皮覆蓋的熊,毛髮的分佈自然平滑而又具有隨機性。然而,texel表達為一個三維陣列,至少在texel空間中,它表現為一個立方體。texel需要連續地對映到熊的形狀上,以避免縫隙。
泰迪熊是使用一種叫做生成模型的新技術來建模的。每個身體部分(頭部,身體,耳朵,手臂,腿部和鼻子)都是通過一個設計一個從矩形(由u,v表示)到世界座標R^3的引數對映![]() 來構建的。如果我們使用多邊形來渲染這隻熊(就像我們對熊鼻子的渲染一樣),我們會把這個矩形切成包含nxm個小正方形的網格,每個網格都會逐頂點按照
來構建的。如果我們使用多邊形來渲染這隻熊(就像我們對熊鼻子的渲染一樣),我們會把這個矩形切成包含nxm個小正方形的網格,每個網格都會逐頂點按照![]() 轉換到世界座標系。最終渲染通過雙線性插值得到的物件(每個正方形近似用兩個三角形表達)。圖3演示了這種方法,為了簡單起見,圖片只顯示兩個維度。可以很容易推廣到三維。
轉換到世界座標系。最終渲染通過雙線性插值得到的物件(每個正方形近似用兩個三角形表達)。圖3演示了這種方法,為了簡單起見,圖片只顯示兩個維度。可以很容易推廣到三維。

texels立方體用同樣的方法對映到世界空間。引數化的矩形被切割成nxm的小正方形,每一部分被對映到世界空間,並且使用texel的基礎進行標識(圖4)(在泰迪熊的例子中,一個texel是在整個表面上不斷複製的)

由可生成的模型定義的對映![]() 僅對於每個texel基定義了會發生什麼。texel的第三維度(高度)也需要對映到世界空間,這一對映決定了熊的毛髮是直立的還是躺下的。將
僅對於每個texel基定義了會發生什麼。texel的第三維度(高度)也需要對映到世界空間,這一對映決定了熊的毛髮是直立的還是躺下的。將![]() 擴充套件到texel第三維度僅需要為texel的角進行定義。一旦texel的角點也被對映,它們就不再是盒子狀的了。此外,相鄰texel之間的間隙也會消失(圖5)。texel的線性插值將在接下來的章節介紹,在此我們假設texel裡向有著相同方向的毛髮為一個角點。
擴充套件到texel第三維度僅需要為texel的角進行定義。一旦texel的角點也被對映,它們就不再是盒子狀的了。此外,相鄰texel之間的間隙也會消失(圖5)。texel的線性插值將在接下來的章節介紹,在此我們假設texel裡向有著相同方向的毛髮為一個角點。
我們建立一個建模的程式,允許設計師來操作texel角點的朝向。這個程式從每個texel的角點開始直接計算(每個texel的角點對應頭皮一個表面法線)。然後建立全域性傅立葉對映來擾動角點。

光線和texels求交
在texel空間中,texel是作為一個立方體存在的。如上所述,我們將texel對映到世界空間中,將立方體的六個面轉化為雙線性塊。光線和texel的交點是通過在世界空間中將光線和六個面相交得到的。
將光線和雙線性塊相交
對於每個雙線性塊的邊緣,包括面體上所有水平和垂直的橫截面都是直接。而雙線性塊的其它其它截面都是二次曲面。因此光線和塊相交計算涉及到二次方程的求解是合理的。
射線可由方程R = at + b(0<=t)定義。三維向量a,b分別代表了原點和射線的方向餘弦。一個雙線性塊可由公式 P = Auv + Bu + Cv + D(0<=u<=1,0<=v<=1)來表達,其中A,B,C,D都是三元組。
射線R和塊P的交點在R = P時產生。我們可以列出以下三個方程:
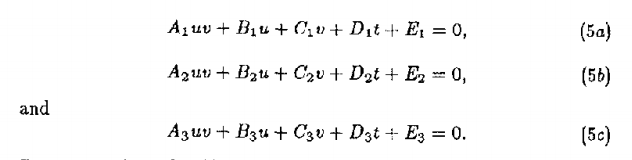
這些方程需要重新排序保證第一個方程有著最大的D係數。這可以保證,在塊與軸對齊的情況下,方程的分母將是合理的(從而避免浮點溢位)。
第一個方程按t來求解:

代入下面兩個方程可以消除t,從而得到兩個方程:

上面兩個方程可以分別乘以F3和F2,然後可以消除uv項,得到一個u,v的線性方程。將u當做一個值可以得到一個關於v的方程,一旦v確定,u便能確定,t也是一樣。
當我們求解這個二元一次方程(形式為ax^2 + bx + c = 0)時,有可能平方項的係數非常小,這在雙線性塊四個點共面的時候可能發生。由於我們只求解0<=u<=1的值,在a的值很小的時候我們可以使用以下式子計算:
![]()
如果方程不成立,則根超過範圍-1 < u < 1,並且不需要計算。這一簡單的測試可以避免浮點數溢位。
將光線-texel交點對映到texel空間
一旦計算出了光線和texel的交點,它們需要對映到texel空間。然後可以通過texel陣列進行三線性插值得到texel的屬性(如密度以及切線向量)。
為了計算對映,我們需要對所有交點進行排序。理想情況下,它們是成對出現的,第一個(近處)表示進入texel的光線,第二個(遠處)表示離開texel的光線。這些交點的形式為(f(near),u(near),v(near),t(near)), 以及(f(far),u(far),v(far),t(far))。其中f是相交面的下標,(u,v)是塊在面f上的座標,t是交點沿著射線的距離。
每個交點都需要重新映射回texel空間,以(x(near),y(near),z(near),t(near)),(x(far),y(far),z(far),t(far))的形式。其中(x,y,z)是交點單元texeld的座標,t值保持不變。
texel空間的交點(x,y,z)座標將會落在一個單位立方體裡,至少有一個分量為0或者1,除了t<0處的交點。在這一例子中,對於t=0時,交點的(x,y,z)座標需要通過插值來校正來匹配射線上的點。
為了渲染場景,shader需要知道在射線上每個點的texel值。因為t引數在從texel空間到世界空間對映的過程是不變的,我們可以使用它插值來計算任意t處的texel空間座標。這三個分量為:

毛髮的光照模型
單個毛髮的光照模型包含兩個組成部分:漫反射和鏡面反射。漫反射是由應用於一個非常小的圓柱體的lambert模型推匯出的,鏡面反射近似於一個應用於圓柱曲面的phong反射模型。
定義光照模型更嚴格的方法是按照Kajiya(1985)、Cabral、Max和Springmeyer(1987)或Krueger(1988)的方式來定義。他們的淪為論文了將微觀表面直接轉換為光照模型的演算法。然而,我們發現光照模型的細節的形式對影象的質量並不那麼關鍵。通過幾個例子測試,我們的預設方法已經足夠了。
繪製毛髮的光照模型的幾何結構如圖6所示。單個毛髮是由位置x0和切線向量t指定的線段。光線L從x0點指向光源。視線向量e指示了散射光向眼睛的方向。所有的向量都將被歸一化。L在垂直於t的平面的投影L'形成了第二個基向量,第三個基的向量b是垂直於前兩個基的向量。

漫反射分量
毛髮的漫反射分量是沿著一個朝向光源的半圓柱體應用Lambert表面模型得到的,如圖7所示,我們在光源可見的半圓形上進行積分。表面的背面未被照亮。我們可以很容易算出三個向量t,l',b構成的正交基。第一個基為t,它垂直於texel單元,第二個基為l',它是光線向量在texel的法線平面上的投影。l'可由下式計算:
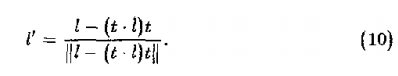
垂直於t和l‘的b的計算方法非常簡單:
![]()
這三個向量在圖6中都有標註。

圓柱單位長度上的光照總量是沿著陰影終端進行半圓形積分(如圖7)。讓我們設當前繞圓柱的角度為![]() ,範圍在0~Pi之間。圓柱的n關於
,範圍在0~Pi之間。圓柱的n關於![]() 的方程為:
的方程為:

lamber模型給出的反射光強為![]()
![]() ,其中kd是漫反射係數。為了求得單位長度上的光的總量,我們沿著半圓形進行積分。沿著圓柱的線性積分元ds可由
,其中kd是漫反射係數。為了求得單位長度上的光的總量,我們沿著半圓形進行積分。沿著圓柱的線性積分元ds可由![]() 來表達,記為
來表達,記為![]() ,因此,可得:
,因此,可得:

kd是和l,l'無關的量。將l'的定義代入上式得到一個漫反射的簡單表示式:

因此,我們得到,漫反射分量和光和切線向量之間的正弦成正比。此時,如果頭髮的正切指向光源,頭髮將是黑色的,這和現實是相符合的。
鏡面反射分量
計算頭髮的高光需要引入映象。我們可以從ad hoc Phong鏡面反射以類似的方法計算。但是,過程會更加困難,結果模型也會相當複雜。因此,我們設計了一種特殊的鏡面模型,它的思想和修改後的Phong模型類似,用於近似模擬頭髮周圍的衍射,該模型在圖8中展現。

任何照向頭髮的光都會沿著切線形成映象角。由於圓柱上的法線垂直於切線的所有方向,所以反射光為獨立於視線的方位角分量。反射光形成一個圓錐,其頂點處的角度等於入射角,如圖8所示,實際上的高光強度可以表達為:
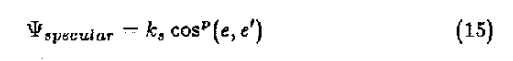
其中,ks是鏡面反射係數,e是指向眼睛的向量,e'是圓錐靠近眼睛向量的鏡面反射向量。p是phong指數,用於指定高光的亮度。當眼睛向量包含在反射椎體,對Phong的依賴下降時,亮度是最大的。
為了計算這一模型,我們注意到,需要計算的唯一量是相對於切線向量的入射角和反射角![]() 和
和![]() :
:
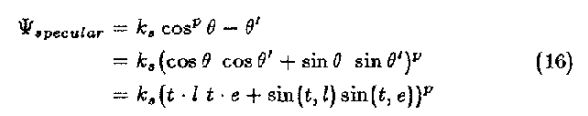
我們可以從原始向量中很快求得這些值。
結果
圖9展現了毛髮的單個texel。除了最基本的平面,沒有使用幾何模型來建立影象。圖10是圖9的近距離觀察,我們發現這裡並不存在畫家視錯覺的現象。我們需要將texel的表達切換到實際的幾何體結構上。
圖11,12,13,14展現了texels轉換後的多個測試影象,繪製的是一個毛絨的表面。這些例子展示了texel的角點沒有經過![]() 變形時的結果。
變形時的結果。
圖11和12是相同的,區別在於11關閉了陰影,所以每個部分都被照亮了。顯然陰影的自遮蔽是texel真實感的重要來源。
圖15和16是泰迪熊的兩個版本,每個熊的幾何模型都是相同的,使用了不同的傅立葉係數來定義每個區域性texel形式。。圖15中使用了更大,更少的texel。每個影象的處理器時間基本相同,解析度都為1280x1024,沒有反走樣處理。
準確的CPU時間測量還有問題,因為每個影象是在大型IBM主機網路上同時渲染的,我們總共使用了12個3090處理器和4個3081處理器,平均下來,每個處理器大致耗費了30%~50%,總時間約為2小時。

更多的工作
將幾何體轉化為文理的問題仍未解決。這篇文章僅僅是該問題的一個開端。一個從任意複雜幾何模型生成texel密度的自動化方法現在仍是無法實現的。我們猜測幾何測量理論可能可以為這個問題提供一些思路。
將texels應用到其他複雜場景的問題也是一個開放的問題:考慮渲染一個山上覆蓋的森林,使用合適的texel為樹和灌木建模,而不使用多邊形。當texels自身非常小時,可以把多個texels合成一個大的texel,從而增加密度併合並照明函式。
我們沒有建模長髮或者捲髮,僅僅考慮了毛皮。這會是一個有趣的建模工作,特別是當我們決定包含動畫的長頭髮的動態行為時,我們相應,一旦建模問題得到解決,本文提出的方法將可以應用到渲染長髮上。
