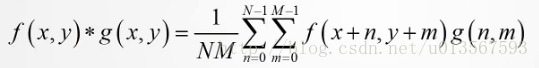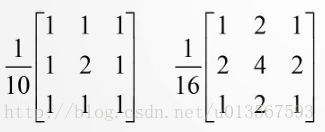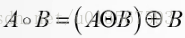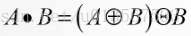影象濾波及去噪初步
定義
說到濾波,不得不提的就是卷積。關於卷積的定義,知乎上有個很有名的段子:

這個話大致講出了卷積的物理意義。
而在影象中,影象濾波的定義也是由卷積進行定義的:
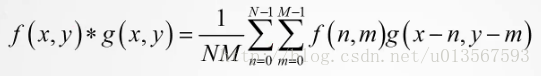
其中f(x,y)是原始影象,g(x,y)是濾波器,他們做卷積的意思是將原始影象與濾波器的視窗對齊後,將其對應位置的元素相乘後,將得到的結果進行累加,最後得到的值即濾波後得到的結果,其位置位於原始影象與濾波器對齊時的視窗中心的位置。如下圖:
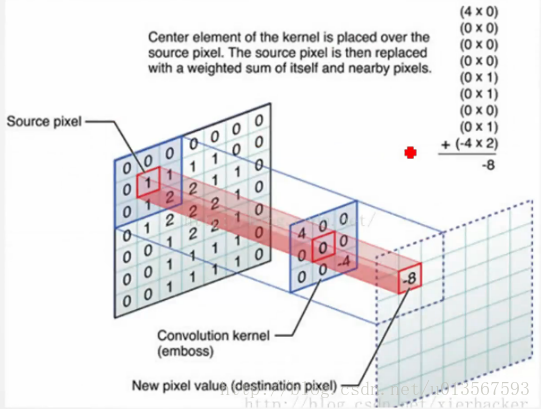
而對於邊緣畫素的處理方法,有一種做法是將原圖邊緣位置擴大一圈並填充以新的元素,新的元素的值與原影象邊緣的值保持一致,這樣一來得到的濾波結果就會比原始影象少一圈,但剛好與擴大之前的原圖尺寸保持一致。
另一個問題,在上式中,g(x-n,y-m)在數學上代表將原始訊號進行了一次左右和上下的反轉,在實際處理時這樣做會造成一些麻煩,每進來一個訊號都要對g進行反轉。為避免這種情況因此我們也經常採用下面的模板形式去定義:
當濾波器對稱時(如圓錐濾波器),兩種定義式是等價的。
去噪
均值濾波
所謂均值濾波顧名思義即對原圖的一個小區域內(如3x3)中所有畫素取平均值:
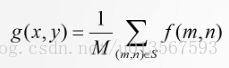
常用的濾波器有4領域,8鄰域及除去自身的8鄰域:
加權平均濾波
加權平均濾波與上面的均值濾波類似,但會做加權平均,即在前面乘上一個對應的係數:
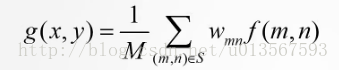
常用的濾波器有2種(3x3),一種是中心點權值是2其餘為1,另一種是高斯濾波器,即中心點權值為4,其4領域的權值為2,其餘為1:
中值濾波
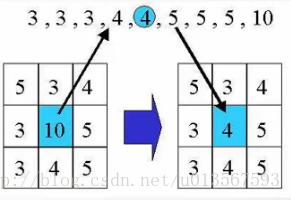
中值濾波與上面的兩種最大的不同之處在於他是一種非線性的濾波方式。這種濾波的步驟通常是:
- 確定濾波視窗及位置(通常含有奇數個畫素)
- 將視窗內的畫素值按灰度大小進行排序
取其中位數代替原視窗中心的畫素值
對比
- 均值濾波能夠濾除白噪聲,但會使原始影象丟掉一些細節(原圖變得模糊)
- 加權均值濾波(高斯濾波)也可以有效的濾除白噪聲,同時不會丟掉原圖中的細節(甚至原圖更清晰)
- 中值濾波可以有效濾除椒鹽噪聲
形態學操作
膨脹
定義:A⊕B膨脹表示集合A用結構元素B去進行膨脹。
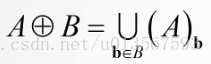
什麼意思。就是說首先結構元素B有一個原點,那麼我們將B放入A中,並將B的原點不斷地對其A的每一個元素,那麼在這種情況下一定有一些元素原先不屬於A,將這種元素併入A中,最後得到的結果即為膨脹後的結果。如圖:
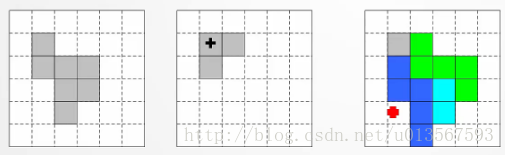
在上圖中,左邊圖為集合A,中間圖為結構元素B,B中標十字的元素為其原點,現在考慮將這個B放在A上,並將B的原點對著A的第一個元素A(2,2),那麼原圖中原先不屬於集合A的元素A(2,3)由於被B覆蓋現在就會被併入集合A,即右圖中的綠色部分。而元素A(3,2)由於原先就屬於A那麼就無需進行操作,即右圖中的藍色部分。不斷地重複此過程,直到將B的原點滑過原集合A的每一個元素。最後得到的結果即為膨脹。
腐蝕
定義:AΘB腐蝕表示集合A用結構元素B去腐蝕。
他的意思就是說還是那麼個集合A和結構元素B,用B的原點去滑過A的每一個元素,在滑的過程中如果B剩下的每一個元素都被原集合A所包含,那麼這個元素即併入腐蝕後的結果,否則直接捨去。如下圖:
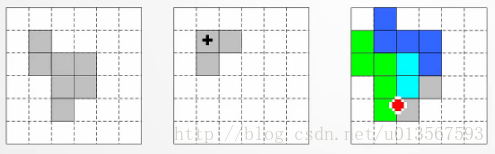
左圖是原集合A,中間圖是結構元素B,右圖中的青色區域即為腐蝕後的結果。
開閉運算
上面值得注意的一點就是,腐蝕和膨脹是對偶操作(不是互逆操作),那麼也就是說若對一幅圖進行膨脹後再腐蝕,得到的並不是原影象。自然而然的,若將二者進行級聯使用便可生成新的形態學運算:
- 開運算:先腐蝕後膨脹
開運算的結果會比原始影象小一些,因為如果原圖中有一個噪聲點,先腐蝕後噪聲點消失,而再膨脹後並不會再膨脹出此噪聲點。故開運算可以減少原圖中的毛刺。 - 閉運算:先膨脹後腐蝕
閉運算的作用是可以將原圖中的小孔給填充上。
由此可以得到一種新的去噪方式:先開後閉。