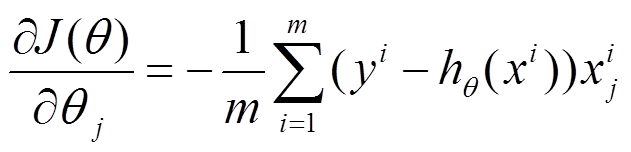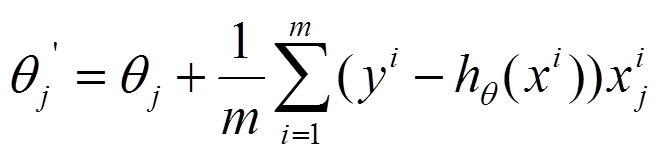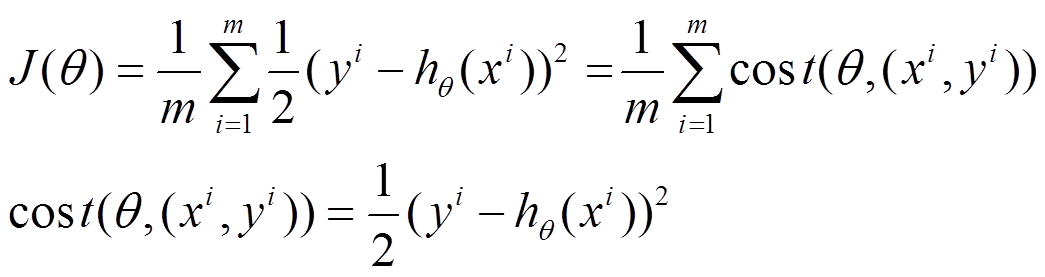1、批量梯度下降的求解思路如下：

（1）將J( θ)對theta求偏導，得到每個 θ對應的的梯度

（2）由於是要最小化風險函式，所以按每個引數theta的梯度負方向，來更新每個theta

（3）從上面公式可以注意到，它得到的是一個全域性最優解，但是每迭代一步，都要用到訓練集所有的資料，如果m很大，那麼可想而知這種方法的迭代速度！！所以，這就引入了另外一種方法，隨機梯度下降。

2、隨機梯度下降的求解思路如下：

（1）上面的風險函式可以寫成如下這種形式，損失函式對應的是訓練集中每個樣本的粒度，而上面批量梯度下降對應的是所有的訓練樣本：

（2）每個樣本的損失函式，對theta求偏導得到對應梯度，來更新theta

（3）隨機梯度下降是通過每個樣本來迭代更新一次，如果樣本量很大的情況（例如幾十萬），那麼可能只用其中幾萬條或者幾千條的樣本，就已經將theta迭代到最優解了，對比上面的批量梯度下降，迭代一次需要用到十幾萬訓練樣本，一次迭代不可能最優，如果迭代10次的話就需要遍歷訓練樣本10次。但是，SGD伴隨的一個問題是噪音較BGD要多，使得SGD並不是每次迭代都向著整體最優化方向。

3、Mini-batch Gradient Descent

（1）這是介於BSD和SGD之間的一種優化演算法。每次選取一定量的訓練樣本進行迭代。

（2）從公式上似乎可以得出以下分析：速度比BSD快，比SGD慢；精度比BSD低，比SGD高。

4、帶Mini-batch的SGD

（1）選擇n個訓練樣本（n<m，m為總訓練集樣本數）

（2）在這n個樣本中進行n次迭代，每次使用1個樣本

（3）對n次迭代得出的n個gradient進行加權平均再並求和，作為這一次mini-batch下降梯度

（4）不斷在訓練集中重複以上步驟，直到收斂。