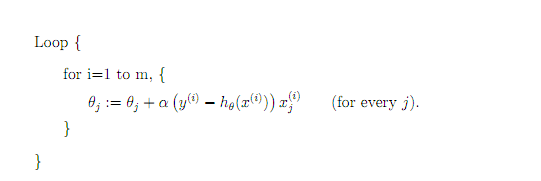一、梯度下降法

　　在機器學習演算法中，對於很多監督學習模型，需要對原始的模型構建損失函式，接下來便是通過優化演算法對損失函式進行優化，以便尋找到最優的引數。在求解機器學習引數的優化演算法中，使用較多的是基於梯度下降的優化演算法(Gradient Descent, GD)。

　　梯度下降法有很多優點，其中，在梯度下降法的求解過程中，只需求解損失函式的一階導數，計算的代價比較小，這使得梯度下降法能在很多大規模資料集上得到應用。梯度下降法的含義是通過當前點的梯度方向尋找到新的迭代點。

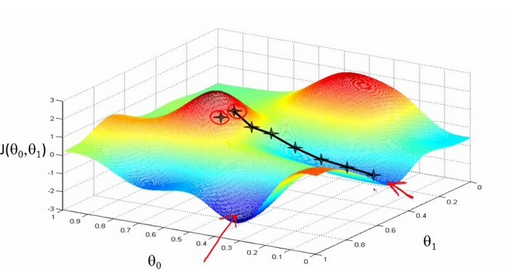
　　基本思想可以這樣理解：我們從山上的某一點出發，找一個最陡的坡走一步（也就是找梯度方向），到達一個點之後，再找最陡的坡，再走一步，直到我們不斷的這麼走，走到最“低”點（最小花費函式收斂點）。
　　

二、梯度下降法的變形形式

　　在具體使用梯度下降法的過程中，主要有以下幾種不同的變種，即：batch、mini-batch、SGD。其主要區別是不同的變形在訓練資料的選擇上。

1、批量梯度下降法BGD
　　批梯度下降法(Batch Gradient Descent)針對的是整個資料集，通過對所有的樣本的計算來求解梯度的方向。
　　批量梯度下降法的損失函式為：
　　
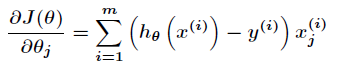
　　進一步得到批量梯度下降的迭代式為：
　　
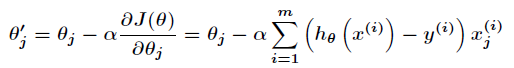
　　每迭代一步，都要用到訓練集所有的資料，如果樣本數目很大，那麼可想而知這種方法的迭代速度！
　　優點：全域性最優解；易於並行實現；
　　缺點：當樣本數目很多時，訓練過程會很慢。
　　從迭代的次數上來看，BGD迭代的次數相對較少。其迭代的收斂曲線示意圖可以表示如下：
　　

2、小批量梯度下降法MBGD
　　在上述的批梯度的方式中每次迭代都要使用到所有的樣本，對於資料量特別大的情況，如大規模的機器學習應用，每次迭代求解所有樣本需要花費大量的計算成本。是否可以在每次的迭代過程中利用部分樣本代替所有的樣本呢？基於這樣的思想，便出現了mini-batch的概念。
　　假設訓練集中的樣本的個數為1000，則每個mini-batch只是其一個子集，假設，每個mini-batch中含有10個樣本，這樣，整個訓練資料集可以分為100個mini-batch。虛擬碼如下：
　　
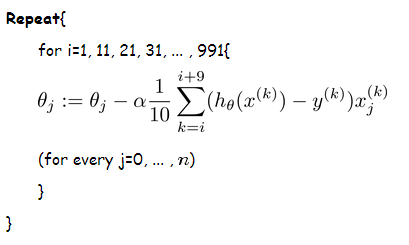
3、隨機梯度下降法SGD

　　隨機梯度下降演算法(stochastic gradient descent)可以看成是mini-batch gradient descent的一個特殊的情形，即在隨機梯度下降法中每次僅根據一個樣本對模型中的引數進行調整，等價於上述的b=1情況下的mini-batch gradient descent，即每個mini-batch中只有一個訓練樣本。
　　隨機梯度下降法的優化過程為：
　　

　　隨機梯度下降是通過每個樣本來迭代更新一次，如果樣本量很大的情況（例如幾十萬），那麼可能只用其中幾萬條或者幾千條的樣本，就已經將theta迭代到最優解了，對比上面的批量梯度下降，迭代一次需要用到十幾萬訓練樣本，一次迭代不可能最優，如果迭代10次的話就需要遍歷訓練樣本10次。但是，SGD伴隨的一個問題是噪音較BGD要多，使得SGD並不是每次迭代都向著整體最優化方向。
　　優點：訓練速度快；
　　缺點：準確度下降，並不是全域性最優；不易於並行實現。
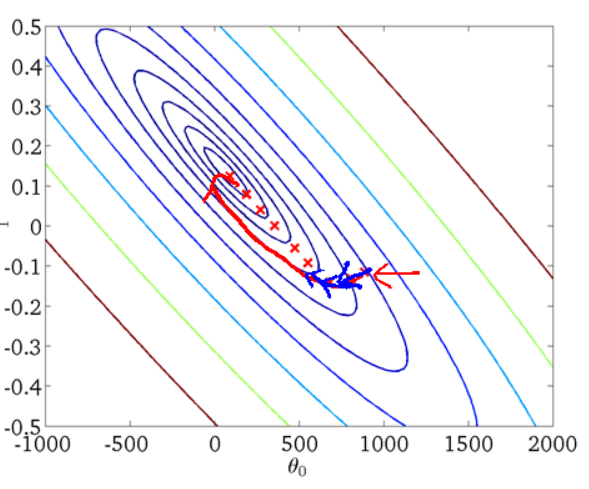
　　從迭代的次數上來看，SGD迭代的次數較多，在解空間的搜尋過程看起來很盲目。其迭代的收斂曲線示意圖可以表示如下：
　　
　　
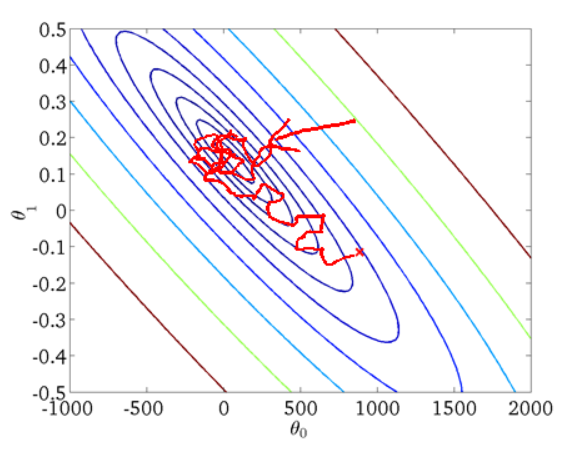
三 、通俗的理解梯度下降

　　（1）批量梯度下降—最小化所有訓練樣本的損失函式（對全部訓練資料求得誤差後再對引數進行更新），使得最終求解的是全域性的最優解，即求解的引數是使得風險函式最小。批梯度下降類似於在山的某一點環顧四周，計算出下降最快的方向（多維），然後踏出一步，這屬於一次迭代。批梯度下降一次迭代會更新所有theta，每次更新都是向著最陡的方向前進。

　　（2）隨機梯度下降—最小化每條樣本的損失函式，雖然不是每次迭代得到的損失函式都向著全域性最優方向， 但是大的整體的方向是向全域性最優解的，最終的結果往往是在全域性最優解附近。隨機也就是說我用樣本中的一個例子來近似我所有的樣本，來調整theta，其不會計算斜率最大的方向，而是每次只選擇一個維度踏出一步；下降一次迭代只更新某個theta，報著並不嚴謹的走走看的態度前進。

四、Batch_Size 的解釋

Batch_Size（批尺寸）是機器學習中一個重要引數，涉及諸多矛盾，下面逐一展開。

1，首先，為什麼需要有 Batch_Size 這個引數？

Batch 的選擇，首先決定的是下降的方向。如果資料集比較小，完全可以採用全資料集 （ Full Batch Learning ）的形式，這樣做至少有 2 個好處：其一，由全資料集確定的方向能夠更好地代表樣本總體，從而更準確地朝向極值所在的方向。其二，由於不同權重的梯度值差別巨大，因此選取一個全域性的學習率很困難。 Full Batch Learning 可以使用 Rprop 只基於梯度符號並且針對性單獨更新各權值。

對於更大的資料集，以上 2 個好處又變成了 2 個壞處：其一，隨著資料集的海量增長和記憶體限制，一次性載入所有的資料進來變得越來越不可行。其二，以 Rprop 的方式迭代，會由於各個 Batch 之間的取樣差異性，各次梯度修正值相互抵消，無法修正。這才有了後來 RMSProp 的妥協方案。

2，既然 Full Batch Learning 並不適用大資料集，那麼走向另一個極端怎麼樣？

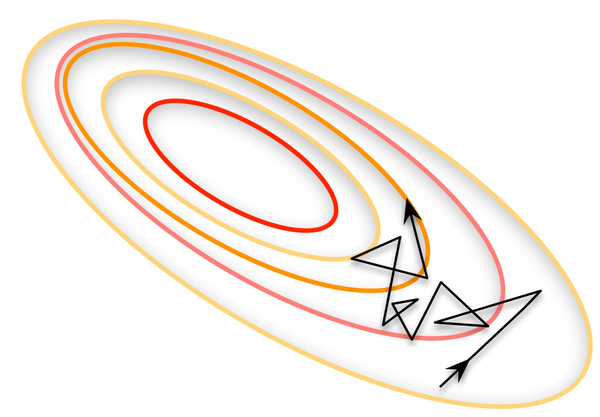
所謂另一個極端，就是每次只訓練一個樣本，即 Batch_Size = 1。這就是線上學習（Online Learning）。線性神經元在均方誤差代價函式的錯誤面是一個拋物面，橫截面是橢圓。對於多層神經元、非線性網路，在區域性依然近似是拋物面。使用線上學習，每次修正方向以各自樣本的梯度方向修正，橫衝直撞各自為政，難以達到收斂。如圖所示：

3，可不可以選擇一個適中的 Batch_Size 值呢？

當然可以，這就是批梯度下降法（Mini-batches Learning）。因為如果資料集足夠充分，那麼用一半（甚至少得多）的資料訓練算出來的梯度與用全部資料訓練出來的梯度是幾乎一樣的。

4，在合理範圍內，增大 Batch_Size 有何好處？

記憶體利用率提高了，大矩陣乘法的並行化效率提高。
跑完一次 epoch（全資料集）所需的迭代次數減少，對於相同資料量的處理速度進一步加快。
在一定範圍內，一般來說 Batch_Size 越大，其確定的下降方向越準，引起訓練震盪越小。

5，盲目增大 Batch_Size 有何壞處？

記憶體利用率提高了，但是記憶體容量可能撐不住了。
跑完一次 epoch（全資料集）所需的迭代次數減少，要想達到相同的精度，其所花費的Batch_Size 增大到一定程度，其確定的下降方向已經基本不再變化。

6，調節 Batch_Size 對訓練效果影響到底如何？

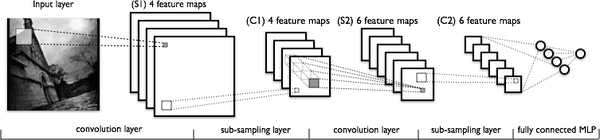
這裡跑一個 LeNet 在 MNIST 資料集上的效果。MNIST 是一個手寫體標準庫，我使用的是 Theano 框架。這是一個 Python 的深度學習庫。安裝方便（幾行命令而已），除錯簡單（自帶 Profile），GPU / CPU 通吃，官方教程相當完備，支援模組十分豐富（除了 CNNs，更是支援 RBM / DBN / LSTM / RBM-RNN / SdA / MLPs）。在其上層有 Keras 封裝，支援 GRU / JZS1, JZS2, JZS3 等較新結構，支援 Adagrad / Adadelta / RMSprop / Adam 等優化演算法。如圖所示：


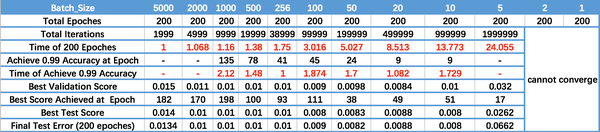
執行結果如上圖所示，其中絕對時間做了標么化處理。執行結果與上文分析相印證：

Batch_Size 太小，演算法在 200 epoches 內不收斂。
隨著 Batch_Size 增大，處理相同資料量的速度越快。
隨著 Batch_Size 增大，達到相同精度所需要的 epoch 數量越來越多。
由於上述兩種因素的矛盾， Batch_Size 增大到某個時候，達到時間上的最優。
由於最終收斂精度會陷入不同的區域性極值，因此 Batch_Size 增大到某些時候，達到最終收斂精度上的最優。