IEEE754浮點數的表示方法
1.浮點數的儲存格式
浮點數在C/C++中對應float和double型別,我們有必要知道浮點數在計算機中實際儲存的內容。
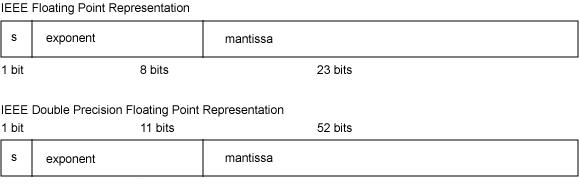
IEEE754標準中規定float單精度浮點數在機器中表示用 1 位表示數字的符號,用 8 位來表示指數,用23 位來表示尾數,即小數部分。對於double雙精度浮點數,用 1 位表示符號,用 11 位表示指數,52 位表示尾數,其中指數域稱為階碼。IEEE 浮點值的格式如下圖所示。
注意,IEE754規定浮點數階碼E採用”指數e的移碼-1”來表示,請記住這一點。為什麼指數移碼要減去1,這是IEEE754對階碼的特殊要求,以滿足特殊情況,比如對正無窮的表示。
2.浮點數的規格化
若不對浮點數的表示作出明確的規定,同一個浮點數的表示就不是唯一的。例如(1.75)10可以表示成1.11×20,0.111×21,0.0111×22等多種形式。當尾數不為0時,尾數域的最高有效位為1,這稱為浮點數的規格化。否則,以修改階碼同時左右移動小數點位置的辦法,使其成為規格化數的形式。
2.1單精度浮點數真值
IEEE754標準中,一個規格化32位的浮點數x的真值表示為:
e=E−127
其中尾數域表示的值是1.M。因為規格化的浮點數的尾數域最左位總是1,故這一位不予儲存,而認為隱藏在小數點的左邊。
在計算指數e時,對階碼E的計算採用原始碼的計算方式,因此32位浮點數的8bits的階碼E的取值範圍是0到255。其中當E為全0或者全1時,是IEEE754規定的特殊情況,下文會另外說明。
2.2雙精度浮點數真值
64位的浮點數中符號為1位,階碼域為11位,尾數域為52位,指數偏移值是1023。因此規格化的64位浮點數x的真值是:
e=E−1023
3.移碼
移碼(又叫增碼)是對真值補碼的符號位取反,一般用作浮點數的階碼,引入的目的是便於浮點數運算時的對階操作。
對於定點整數,計算機一般採用補碼的來儲存。正整數的符號位為0,反碼和補碼等同於原始碼。
負整數符號位都固定為1,原始碼,反碼和補碼的表示都不相同,由原碼錶示法變成反碼和補碼有如下規則:
(1)原始碼符號位為1不變,整數的每一位二進位制數位求反得反碼;
(2)反碼符號位為1不變,反碼數值位最低位加1得補碼。
比如,以一個位元組8bits來表示-3,那麼[−3]原=10000011,[−3]反=11111100,[−3]補=11111101,那麼-3的移碼就是[−3]移=01111101。
如何將移碼轉換為真值-3呢?先將移碼轉換為補碼,再求值。
4.浮點數的具體表示
4.1十進位制到機器碼
(1)0.5
0.5=(0.1)2,符號位S為0,指數為e=−1,規格化後尾數為1.0。
單精度浮點數尾數域共23位,右側以0補全,尾數域:
階碼E:
對照單精度浮點數的儲存格式,將符號位S,階碼E和尾數域M存放到指定位置,得0.5的機器碼:
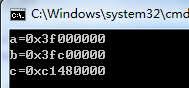
十六進位制表示為0.5=0x3f000000。
(2)1.5
1.5=[1.1]2,符號位為0,指數e=0,規格化後尾數為1.1。
尾數域M右側以0補全,得尾數域:
階碼E:
得1.5的機器碼:
十六進位制表示為1.5=0x3fc00000。
(3)-12.5
−12.5=[−1100.1]2,符號位S為1,指數e為3,規格化後尾數為1.1001,
尾數域M右側以0補全,得尾數域:
階碼E:
即-12.5的機器碼:
十六進位制表示為-12.5=0xc1480000。
用如下程式驗證上面的推算,程式碼編譯執行平臺Win32+VC++ 2012:
#include <iostream>
using namespace std;
int main(){
float a=0.5;
float b=1.5;
float c=-12.5;
unsigned int* pa=NULL;
pa=(unsigned int*)&a;
unsigned int* pb=NULL;
pb=(unsigned int*)&b;
unsigned int* pc=NULL;
pc=(unsigned int*)&c;
cout<<hex<<"a=0x"<<*pa<<endl;
cout<<hex<<"b=0x"<<*pb<<endl;
cout<<hex<<"c=0x"<<*pc<<endl;
return 0;
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
輸出結果:
驗證正確。
4.2機器碼到十進位制
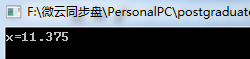
(1)若浮點數x的IEEE754標準儲存格式為0x41360000,那麼其浮點數的十進位制數值的推演過程如下:
0x41360000=[01000001001101100000000000000000]根據該浮點數的機器碼得到符號位S=0,指數e=階碼-127=1000 0010-127=130-127=3。
注意,根據階碼求指數時,可以像上面直接通過 “階碼-127”求得指數e,也可以將階碼+1=移碼,再通過移碼求其真值便是指數e。比如上面階碼10000010+1=10000011[移碼]=>00000011[補]=3(指數e)。
包括尾數域最左邊的隱藏位1,那麼尾數1.M=1.011 0110 0000 0000 0000 0000=1.011011。
於是有:
通過程式碼同樣可以驗證上面的推算:
#include <iostream>
using namespace std;
int main(){
unsigned int hex=0x41360000;
float* fp=(float*)&hex;
cout<<"x="<<*fp<<endl;
return 0;
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
輸出結果:
驗證正確。
5.浮點數的幾種特殊情況
(1)0的表示
對於階碼為0或255的情況,IEEE754標準有特別的規定:
如果 階碼E=0並且尾數M是0,則這個數的真值為±0(正負號和數符位有關)。
因此+0的機器碼為:0 00000000 000 0000 0000 0000 0000。
-0的機器碼為:1 00000000 000 0000 0000 0000 0000。
需要注意一點,浮點數不能精確表示0,而是以很小的數來近似表示0。因為浮點數的真值等於(以32bits單精度浮點數為例):
e=E−127
那麼+0的機器碼對應的真值為1.0×2−127。同理,-0機器碼真值為−1.0×2−127。
(2)+∞和−∞的表示
如果階碼E=255 並且尾數M全是0,則這個數的真值為±∞(同樣和符號位有關)。因此+∞的機器碼為:0 11111111 000 0000 0000 0000 0000。-∞的機器嗎為:1 11111111 000 0000 0000 0000 0000。
(3)NaN(Not a Number)
如果 E = 255 並且 M 不是0,則這不是一個數(NaN)。
6.浮點數的精度和數值範圍
6.1浮點數的數值範圍
根據上面的探討,浮點數可以表示-∞到+∞,這只是一種特殊情況,顯然不是我們想要的數值範圍。
以32位單精度浮點數為例,階碼E由8位表示,取值範圍為0-255,去除0和255這兩種特殊情況,那麼指數e的取值範圍就是1-127=-126到254-127=127。
(1)最大正數
因此單精度浮點數最大正數值的符號位S=0,階碼E=254,指數e=254-127=127,尾數M=111 1111 1111 1111 1111 1111,其機器碼為:0 11111110 111 1111 1111 1111 1111 1111。
那麼最大正數值:
這是一個很大的數。
(2)最小正數
最小正數符號位S=0,階碼E=1,指數e=1-127=-126,尾數M=0,其機器碼為0 00000001 000 0000 0000 0000 0000 0000。
那麼最小正數為:
相關推薦
IEEE754浮點數的表示方法
1.浮點數的儲存格式 浮點數在C/C++中對應float和double型別,我們有必要知道浮點數在計算機中實際儲存的內容。 IEEE754標準中規定float單精度浮點數在機器中表示用 1 位表示數字的符號,用 8 位來表示指數,用23 位來表示尾數,即小數部分。對於dou
-1.1的浮點數表示(IEEE754標準)
‐1.1 = ‐1.00011 [0011]...B = ‐1.00011001100110011001100B(注:尾數取 23 位) 符號位 S = 1,階碼 exp= 0 + 127 = 0111 1111,尾數:00011001100110011001100 則其
java 浮點數表示詳解及解決方法(例項函式)
定點數表達法的缺點在於其形式過於僵硬,固定的小數點位置決定了固定位數的整數部分和小數部分,不利於同時表達特別大的數或者特別小的數。 計算機系統採納了所謂的浮點數表達方式。這種表達方式利用科學計數法來表達實數,即用一個尾數(Mantissa也叫有效數字 ),一個基數(Base
C# IEEE754浮點數的轉換方法
ref: https://blog.csdn.net/jvouge/article/details/589417416進位制轉換為10進位制的公式如下: SGL = (-1)^SIGN * 1.MANTISSA * 2^(EXPONENT-127)1。位元組轉換為浮點數int
IEEE754標準浮點數表示與舍入
原文地址:[https://blog.fanscore.cn/p/26/](https://blog.fanscore.cn/p/26/) > 友情提示:本文排版不太好,但內容簡單,請耐心觀看,總會搞懂的。 # 1. 定點數 對於一個無符號二進位制小數,例如`101.111`,如果我們要用2個位元組
float與 double型數據存儲---IEEE浮點數表示法
0.12 理解 float 標準 顯示 運算 details .com c/c++ 目前C/C++編譯器標準都遵照IEEE制定的浮點數表示法來進行float,double運算。 這種結構是一種科學計數法,用符號、指數和尾數來表示,底數定為2——即把一個浮點數表示為尾數乘以2
IEEE754浮點數即其加法
參考:《計算機組成與設計(原書第5版)》 中國大學MOOC,國防科技大學的《計算機原理》課程 浮點數加法步驟 • A=Ma * 2^a,B=Mb * 2^b, Ea≥Eb:
機器中的浮點數表示
在初學C語言時,一直體會不到所謂的浮點數容易造成誤差,最近看到一篇關於浮點數的文章,加上現在的學習,對浮點數的內部儲存方式有了更加深入的理解,於是也漸漸理解了浮點數的誤差。 相比int等整型,float等浮點型別的表示和儲存較為複雜,但它又是一
計組—浮點數表示和運算
浮點數的表示 科學計數法 任意一個十進位制數N可以寫成: 同樣,在計算機中一個任意進位制數N可以寫成 在計算機的世界裡R預設是2,表示二進位制,因此R在計算機中不用單獨儲存,而M和e需要單獨儲存 尾數(M):用定點小數表示,給出有效數字的位數,決定了浮點
CS:APP3e Homework 2.97 關於整型轉單精度浮點數的方法討論
CS:APP3e Homework 2.97 關於整型轉單精度浮點數的方法討論 關於整型轉單精度浮點數的方法討論 CS:APP原題 題目分析 實現程式碼 原理解釋 其他方法 啟示與思考 關
IEEE754浮點數轉換
IEEE754規定如下的計算方法, 計算公式: V=(-1)^s*2^E*M 當e(各位)為全'0'時,E=1-(2^(e(位數)-1)-1),;M=m。 如:real*4是8位,E=1-(2^(8-1)-1)=1-127=-126 即,
IEEE浮點數表示
IEEE浮點標準:V=(-1)^s*M*2^E 1.符號(sign)s決定這個數是負數(s=1)還是正數,0(s=0)。 2.尾數(significand) M是一個二進位制小數. 3.階碼(exponent)E對浮點數加權。 單精度,雙精度的表示如下
關於IEEE754浮點數階碼
問題: 1、為什麼和定點數的移碼偏置值不同,定點數是2^n,浮點數是2^n-12、而且為什麼範圍是1~254(8位),按理說不應該是0~255嗎? 回答: IEEE754浮點數表示方法:(-1)^s * 1.M * 2^(E-127) 對於階碼為0或255的情況,IEEE7
c/c++中的浮點數的表示方法
轉自:http://www.cnblogs.com/dolphin0520/archive/2011/10/02/2198280.html 任何資料在記憶體中都是以二進位制的形式儲存的,例如一個short型資料1156,其二進位制表示形式為00000100 100001
IEEE 754——計算機中浮點數的表示方法
楔子 #include <iostream> int main(int, char**) { std::cout.precision(20); float a = 123.45678901234567890;
IEEE 754 浮點數的表示精度探討
選擇 固定 images 方向 post 可用 分用 lan text IEEE 754 浮點數的表示精度探討 前言 從網上看到不少程序猿對浮點數精度問題有非常多疑問,在論壇上發貼詢問。非常多熱心人給予了解答,但我發現一些解答中有些許小的錯誤和認識不
浮點數的二進制表示
命令 如果 initial 計算機 做的 大於 round 得到 pre 轉載自:http://www.ruanyifeng.com/blog/2010/06/ieee_floating-point_representation.html 前幾天,我在讀一本C語言教
cout<<fixed表示按一般方式輸出浮點數
AI pan bsp style int double spa end turn int main() { double num=0.00001; cout<<num<<endl; cout<<fixe
JVM之浮點數(float)表示
img 但是 nbsp alt 符號 否則 形式 十進制 浮點數 1. 浮點數的組成:符號位、指數位、尾數位。 1.1 符號位: 占1位,表示正負數; 1.2 指數位: 占8位; 1.3 尾數位: 占23位。 2. 浮點數的表示: 2.1
浮點數是如何表示的
如何編碼浮點數?我們知道計算機表示的任何資訊都是一串bit,具體內容決定於如何解釋。IEEE浮點標準用 V = (-1)^s * M * 2^E 的形式來表示一個數。s表示符號(1表示負,0表示正); M表示尾數,二進位制小數,取值範圍為1~2或者0~1,不包括上限值;E表示階碼