1.正式開始之前的描述

(1)

PLA：Perceptron Learning Algorithm。
在正式開始之前，我想先說一下，PLA到底是幹嘛的。大部分機器學習的書以及視訊都是以感知機演算法作為開頭的。既然放在最前面，它應該就是一個很簡單的機器學習演算法。事實上，它確實很簡單。
如下圖所示: 紅色和藍色的點分別表示訓練集中的正樣本和負樣本，PLA的任務就是尋找下面那條能將訓練集完全分開的藍色直線。(一般簡單的認為，這個樣本的類別是-1，那它就是負樣本；反之，它就是正樣本。正負樣本共同構成訓練集。)
注：圖片是從這篇部落格盜的，(:|。

http://blog.sina.com.cn/s/blog_59fabe030101ji4r.html

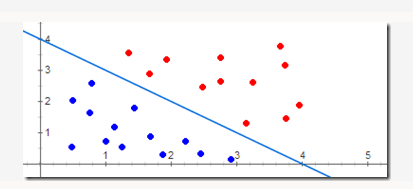
注意：這裡只是為了方便理解，我們才用二維座標系下的點表示樣本。事實上，樣本的特徵的維度往往要比2大的多，想象一下一個6維的點，我們很難去用圖形化的方式把它表示出來。

(2)

說了PLA是幹什麼的之後，我把正式開始PLA之前需要說清楚的一些概念先寫出來。

我們的訓練集裡面有N個樣本，trainingSet={(X1,Y1),(X2,Y2),...,(XN,YN)}
(Xi,Yi)表示第i個樣本，這個樣本是由特徵和標籤(label)構成。
第i個樣本的特徵是：Xi=[xi1,xi2,...,xin],Xi是一個n維的向量，我們在這裡假設樣本的特徵是n維的。
第i個樣本的標籤(label)是：Y

i∈{+1,−1}，Yi是+1或者-1。

！！！！一定要分清楚X和x,一定要分清楚上標和下標(上標表示第幾個樣本，下標表示這個樣本的第幾個特徵)，一定要區分清楚樣本和特徵的概念,一定要分清楚N和n所表示的含義的不同(N表示樣本數量，n表示特徵的數量)！！！！

！！！！一定要分清楚X和x,一定要分清楚上標和下標(上標表示第幾個樣本，下標表示這個樣本的第幾個特徵)，一定要區分清楚樣本和特徵的概念,一定要分清楚N和n所表示的含義的不同(N表示樣本數量，n表示特徵的數量)！！！！

！！！！一定要分清楚X和x,一定要分清楚上標和下標(上標表示第幾個樣本，下標表示這個樣本的第幾個特徵)，一定要區分清楚樣本和特徵的概念,一定要分清楚N和n所表示的含義的不同(N表示樣本數量，n表示特徵的數量)！！！！

如果你對！！！！所說的內容有所疑惑的話，請暫停你前進的步伐，先百度把這幾個問題弄清楚，這個真的很重要。

(3)

PLA的輸出模型(也叫作目標函式)：h(X)=sign(WX+b)
注：W是一個n維的行向量，通常叫做權值向量，W=[w1,w2,....wn]。
X是一個n維的列向量，是樣本特徵,X=[x1,x2,...,xn]T。
sign函式：當k>0時,sign(k)=+1;當k<0時,sign(k)=-1。
（每次說到輸出模型，我總會想多叨嘮幾句，以確保看者能理解我想表達的意思。在PLA中輸出模型是h(X)函式，我們可以發現：只要我們知道了引數W和b，那麼h(X)也就可以確定了。所以可以說PLA演算法真正的輸出是W和b。能為了讓表述更系統化，我們通常都會說輸出模型是h(X)函式。）

W和X是兩個向量，我們做如下改寫：
W=[b,w1,w2,....wn];X=[1,x1,x2,...,xn]T
那麼原來的WX+b就可以直接寫成WX了。為了方便我們的描述，在本文如果沒有特別說明，都會沿用這種表達方式。

我們在(1)說了，PLA的任務是找到那條能把訓練樣本正確分類的直線（現在可以直觀的看出來，它不是一條直線那麼簡單了吧。在(1)中，只是為了方便描述，我們才把X的維度設定為2。當X的維度>2時，WX所表示的就是一個平面了，我們通常稱這個平面為分隔(分離)超平面）。

我覺得有必要先說一下,我們得到一個模型，這個模型怎麼用？
假設現在我們通過PLA演算法已經求得了一個模型。現在需要去預測一個不知道標籤的樣本的標籤是多少？
我們把這個樣本的特徵X帶入到h(X)中，h(X)就會等於+1或者-1(這個模型判斷的這個樣本最有可能屬於哪個類別)，我們就預測出來這個樣本的標籤了。

2.正式的描述PLA演算法

假設訓練資料集是線性可分的（可以通過一條直線或者一個平面將訓練集完全分類正確）。
PLA演算法流程：
輸入：訓練資料集{(X1,Y1),(X2,Y2),...,(XN,YN)}
輸出：W
(1)選取初值W0
(2)從訓練集中選取樣本(Xi,Yi)
(3)更新。如果Yi(WtXi)≤0, 則Wt+1=Wt+ηYiXi
(4)轉至(2),直至訓練集中的所有樣本被完全正確分類。

注：
1.在(1)中，我們總是喜歡令W0=0。初始值是隨便選的，只是通常人們總是喜歡從0開始。
2.在(3)中，如果Yi(WtXi)≤0，這是什麼意思？
如果sign(WtXi)≠Yi.我們在這個時候就稱以這個Wt為引數的模型錯誤分類了這個樣本。
sign(WtXi)≠Yi的等價的寫法是Y

相關推薦

機器學習總結2_感知機演算法(PLA)

1.正式開始之前的描述 (1) PLA：Perceptron Learning Algorithm。 在正式開始之前，我想先說一下，PLA到底是幹嘛的。大部分機器學習的書以及視訊都是以感知機演算法作為開頭的。既然放在最前面，它應該就是一個很簡單的機器學

機器學習入門實戰——感知機演算法實戰Iris資料集

感知機演算法實戰Iris資料集 關於感知機的相關理論知識請檢視：感知機 關於Iris資料集 Iris也稱鳶尾花卉資料集，是一類多重變數分析的資料集。資料集包含150個數據集，分為3類，每類50個數據，每個資料包含4個屬性。可通過花萼長度，花萼寬度，花

機器學習演算法【感知機演算法PLA】【5分鐘讀完】

本來想說3分鐘可以讀完的，但是想到自己的表達水平。我覺得可能需要多出2分鐘來理解我說的話。 感知機演算法 一開始這個名字，不懂的人覺得這個逼格很高，感覺很厲害的樣子，其實這個演算法很水的…. 對於這個演算法，我們只需要知道下面這幾樣東西： 1.

機器學習第一站——感知機

話不多說，先上圖： 看完這個圖相信大家對感知機會有一個比較感性的認識：可以根據不同點的顏色用一條線將整個圖形平面劃分為兩個區域。 這聽起來對我們來說是非常容易的（目測一下就大概知道該怎麼劃線），但對於一個機器或電腦呢，他們是怎麼知道這條線該劃在哪？怎麼保

記一下機器學習筆記 Rosenblatt感知機

一入ML深似海啊… 這裡主要是《神經網路與機器學習》（Neural Networks and Learning Machines，以下簡稱《神機》）的筆記，以及一些周志華的《機器學習》的內容，可能夾雜有自己的吐槽，以及自己用R語言隨便擼的實現。 話說這個《神

《李航：統計學習方法》--- 感知機演算法原理與實現

感知機模型 感知機是一個二類分類的線性分類模型。所謂二類分類就是它只能將例項分為正類和負類兩個類別。那麼為什麼是線性分類模型呢，我的理解是感知機學習旨在求出可以將資料進行劃分的分離超平面，而分離超平面的方程 w⋅x+b=0 為線性方程，所以感知機為線性分類模型

機器學習之支援向量機演算法例項

此例項是利用svm演算法預測乳腺癌腫瘤是良性還是惡性，資料格式如下圖所示：第一列表示編號，2到10列表示資料屬性，第11列表示腫瘤標籤2表示良性4表示惡性。 程式碼如下 from sklearn import svm # x = [[2, 0], [1, 1], [

機器學習之支援向量機演算法(一)

一、問題引入 　　支援向量機(SVM，Support Vector Machine)在2012年前還是很牛逼的，但是在12年之後神經網路更牛逼些，但是由於應用場景以及應用演算法的不同，我們還是很有必要了解SVM的，而且在面試的過程中SVM一般都會問到。支援向量機是一個非常經典且高效的分類模型。我們的目標：基

機器學習之支援向量機演算法(二)

五、SVM求解例項 　　上面其實已經得出最終的表示式了，下面我們會根據一些具體的點來求解α的值。資料：3個點，其中正例 X1(3,3) ，X2(4,3) ，負例X3(1,1) 如下圖所示 　　　 　　我們需要求解下式的極小值 　　　 　　注意約束條件（在這裡不要忘記了yi代表的是資料

教你6步從頭寫機器學習演算法——以感知機演算法為例

自己從頭寫一個演算法，不僅能給你帶來成就感，也能幫你真正理解演算法的原理。可能你之前用 Scikit-learn 實現過演算法，但是從零開始寫個演算法簡單嗎？絕對不簡單。 有些演算法要比其它演算法複雜的多，所以在寫演算法時可以先從簡單的開始，比如單層的感知機。 下面就介紹機器學家 John S

機器學習演算法原理與實踐（六）、感知機演算法

感知機 感知機是二分類的線性分類模型，輸入為例項的特徵向量，輸出為例項的類別（取+1和-1）。感知機對應於輸入空間中將例項劃分為兩類的分離超平面。感知機旨在求出該超平面，為求得超平面匯入了基於誤分類的損失函式，利用梯度下降法對損失函式進行最優化（最優

機器學習筆記（1） 感知機演算法 之 實戰篇

我們在上篇筆記中介紹了感知機的理論知識，討論了感知機的由來、工作原理、求解策略、收斂性。這篇筆記中，我們親自動手寫程式碼，使用感知機演算法解決實際問題。 先從一個最簡單的問題開始，用感知機演算法解決OR邏輯的分類。 import numpy as np import matplotlib.pyplot as

機器學習總結（八）決策樹ID3，C4.5演算法，CART演算法

本文主要總結決策樹中的ID3,C4.5和CART演算法，各種演算法的特點，並對比了各種演算法的不同點。 決策樹：是一種基本的分類和迴歸方法。在分類問題中，是基於特徵對例項進行分類。既可以認為是if-then規則的集合，也可以認為是定義在特徵空間和類空間上的條件概率分佈。 決策樹模型：決策樹由結點和有向邊組

《機器學習實戰》學習總結1——K-近鄰演算法

新手入門學習機器學習，根據ApacheCN的視訊學習程式碼，視訊可以在bilibili線上播放。 有需要資料的可以在GitHub下載：https://github.com/RedstoneWill/MachineLearning 本文最主要的是分析程式碼的功能與實現，相應的原理大家拿看就好了

NG機器學習總結-（七）SVM支援向量機

一、損失函式 在邏輯迴歸中，我們的預測函式和損失函式為： 預測函式： 損失函式： 我們知道當y分別是1和0的時候，其cost函式如下黑色曲線部分： 不難看出，當 y=1時，隨著 z 取值變大，預測損失變小，因此，邏輯迴歸想要在面對正樣本 y=1時

《機器學習實戰》學習總結1——K-近鄰演算法（程式清單2-1）

程式碼如下： def classify0(inX, dataSet, labels, k): # inX是用於分類的輸入向量，dataSet是輸入的訓練樣本集，lebels是標籤向量，k是用於選擇最近鄰居的數目 dataSetSiz

機器學習總結（十）：常用聚類演算法（Kmeans、密度聚類、層次聚類）及常見問題

任務：將資料集中的樣本劃分成若干個通常不相交的子集。 效能度量：類內相似度高，類間相似度低。兩大類：1.有參考標籤，外部指標；2.無參照，內部指標。 距離計算：非負性，同一性（與自身距離為0），對稱性

機器學習之支援向量機SVM Support Vector Machine (五) scikit-learn演算法庫

一、scikit-learn SVM演算法庫概述         scikit-learn中SVM的演算法庫分為兩類，一類是分類演算法庫，包括SVC、 NuSVC和LinearSVC三個類。另一類是迴歸演算法庫，包括SVR、NuSVR和LinearSVR三個類。相關的

機器學習總結 選擇一個合適的演算法

演算法的分類 收集的一個很實用的思維導圖 SKlearn的演算法地圖 具體地址：http://scikit-learn.org/stable/tutorial/machine_learning_m

機器學習總結（三）：SVM支援向量機（面試必考）

基本思想：試圖尋找一個超平面來對樣本分割，把樣本中的正例和反例用超平面分開，並儘可能的使正例和反例之間的間隔最大。 演算法推導過程： （1）代價函式：假設正類樣本y =wTx+ b>=+1,負