二分圖的概念

二分圖又稱作二部圖，是圖論中的一種特殊模型。
設G=(V, E)是一個無向圖。如果頂點集V可分割為兩個互不相交的子集X和Y，並且圖中每條邊連線的兩個頂點一個在X中，另一個在Y中，則稱圖G為二分圖。

二分圖的性質

定理：當且僅當無向圖G的每一個迴路的次數均是偶數時，G才是一個二分圖。如果無迴路，相當於任一回路的次數為0，故也視為二分圖。

二分圖的判定

如果一個圖是連通的，可以用如下的方法判定是否是二分圖：
在圖中任選一頂點v，定義其距離標號為0，然後把它的鄰接點的距離標號均設為1，接著把所有標號為1的鄰接點均標號為2（如果該點未標號的話），如圖所示，以此類推。
標號過程可以用一次BFS實現。標號後，所有標號為奇數的點歸為X部，標號為偶數的點歸為Y部。
接下來，二分圖的判定就是依次檢查每條邊，看兩個端點是否是一個在X部，一個在Y部。
如果一個圖不連通，則在每個連通塊中作判定。

二分圖匹配

給定一個二分圖G，在G的一個子圖M中，M的邊集{E}中的任意兩條邊都不依附於同一個頂點，則稱M是一個匹配。
圖中加粗的邊是數量為2的匹配。

最大匹配

選擇邊數最大的子圖稱為圖的最大匹配問題(maximal matching problem)
如果一個匹配中，圖中的每個頂點都和圖中某條邊相關聯，則稱此匹配為完全匹配，也稱作完備匹配。
圖中所示為一個最大匹配，但不是完全匹配。

增廣路徑

增廣路徑的定義：設M為二分圖G已匹配邊的集合，若P是圖G中一條連通兩個未匹配頂點的路徑（P的起點在X部，終點在Y部，反之亦可），並且屬M的邊和不屬M的邊(即已匹配和待匹配的邊)在P上交替出現，則稱P為相對於M的一條增廣路徑。
增廣路徑是一條“交錯軌”。也就是說, 它的第一條邊是目前還沒有參與匹配的,第二條邊參與了匹配,第三條邊沒有..最後一條邊沒有參與匹配,並且起點和終點還沒有被選擇過，這樣交錯進行,顯然P有奇數條邊（為什麼？）

尋找增廣路

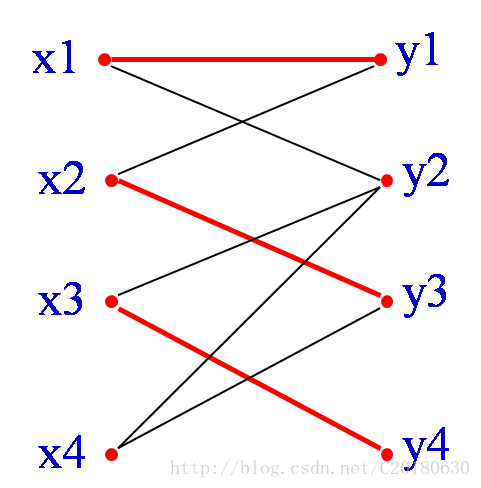
紅邊為三條已經匹配的邊。從X部一個未匹配的頂點x4開始，找一條路徑：
x4,y3,x2,y1,x1,y2
因為y2是Y部中未匹配的頂點，故所找路徑是增廣路徑。
其中有屬於匹配M的邊為{x2,y3},{x1,y1}
不屬於匹配的邊為{x4,y3},{x2, y1}, {x1,y2}
可以看出：不屬於匹配的邊要多一條！

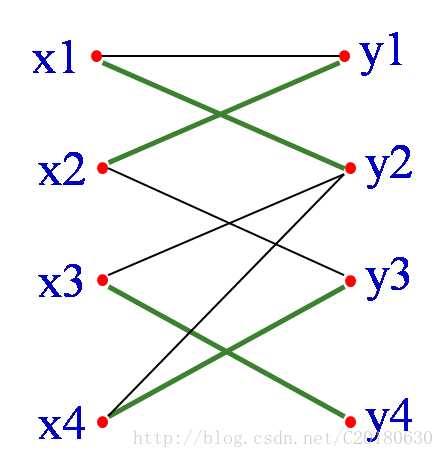
如果從M中抽走{x2,y3},{x1,y1}，並加入{x4,y3},{x2, y1}, {x1,y2}，也就是將增廣路所有的邊進行”反色”,則可以得到四條邊的匹配M’={{x3,y4}, {x4,y3},{x2, y1}, {x1,y2}}
容易發現這樣修改以後,匹配仍然是合法的,但是匹配數增加了一對。另外,單獨的一條連線兩個未匹配點的邊顯然也是交錯軌.可以證明,當不能再找到增廣軌時,就得到了一個最大匹配.這也就是匈牙利演算法的思路.
可知四條邊的匹配是最大匹配

增廣路徑性質

由增廣路的定義可以推出下述三個結論：

1. P的路徑長度必定為奇數，第一條邊和最後一條邊都不屬於M，因為兩個端點分屬兩個集合，且未匹配。
2. P經過取反操作可以得到一個更大的匹配M’。
3. M為G的最大匹配當且僅當不存在相對於M的增廣路徑。

匈牙利演算法

用增廣路求最大匹配(稱作匈牙利演算法，匈牙利數學家Edmonds於1965年提出)
演算法輪廓：

1. 置M為空
2. 找出一條增廣路徑P，通過取反操作獲得更大的匹配M’代替M
3. 重複2操作直到找不出增廣路徑為止

找增廣路徑的演算法

我們採用DFS的辦法找一條增廣路徑：
從X部一個未匹配的頂點u開始，找一個未訪問的鄰接點v（v一定是Y部頂點）。對於v，分兩種情況：

1. 如果v未匹配，則已經找到一條增廣路
2. 如果v已經匹配，則取出v的匹配頂點w(w一定是X部頂點)，邊(w,v)目前是匹配的，根據“取反”的想法，要將(w,v)改為未匹配，(u,v)設為匹配，能實現這一點的條件是看從w為起點能否新找到一條增廣路徑P’。如果行，則u-v-P’就是一條以u為起點的增廣路徑。

匈牙利演算法

cx[i]表示與X部i點匹配的Y部頂點編號
cy[i]表示與Y部i點匹配的X部頂點編號

//虛擬碼
bool dfs(int u)//尋找從u出發的增廣路徑
{
    for each v∈u的鄰接點
        if(v未訪問){
            標記v已訪問;
            if(v未匹配||dfs(cy[v])){
                cx[u]=v;
                cy[v]=u; 
                return true;//有從u出發的增廣路徑
            }
        }
    return false;//無法找到從u出發的增廣路徑
}
//程式碼
bool dfs(int u){
    for(int v=1;v<=m;v++)
        if(t[u][v]&&!vis[v]){
            vis[v]=1;
            if(cy[v]==-1||dfs(cy[v])){
                cx[u]=v;cy[v]=u;
                return 1;
            }
        }
    return 0;
}
void maxmatch()//匈牙利演算法主函式
{
    int ans=0;
    memset(cx,0xff,sizeof cx);
    memset(cy,0xff,sizeof cy);
    for(int i=0;i<=nx;i++) 
        if(cx[i]==-1)//如果i未匹配
        { 
            memset(visit,false,sizeof(visit)) ; 
            ans += dfs(i); 
        }
    return ans ;
} 

演算法分析

演算法的核心是找增廣路徑的過程DFS
對於每個可以與u匹配的頂點v，假如它未被匹配，可以直接用v與u匹配；
如果v已與頂點w匹配，那麼只需呼叫dfs(w)來求證w是否可以與其它頂點匹配，如果dfs(w)返回true的話，仍可以使v與u匹配；如果dfs(w)返回false,則檢查u的下一個鄰接點…….
在dfs時，要標記訪問過的頂點（visit[j]=true），以防死迴圈和重複計算；每次在主過程中開始一次dfs前，所有的頂點都是未標記的。
主過程只需對每個X部的頂點呼叫dfs，如果返回一次true，就對最大匹配數加一；一個簡單的迴圈就求出了最大匹配的數目。

時空分析

• 時間複雜度：
  
  • 找一次增廣路徑的時間為：
    
    • 鄰接矩陣： O(n^2)
    • 鄰接表：O(n+m)
  • 總時間：
    
    • 鄰接矩陣：O(n^3)
    • 鄰接表：O(nm)
• 空間複雜度：
  
  • 鄰接矩陣：O(n^2)
  • 鄰接表： O(m+n)