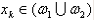判別函式（七）勢函式法
用勢函式的概念來確定判別函式和劃分類別介面。
基本思想
假設要劃分屬於兩種類別ω1和ω2的模式樣本，這些樣本可看成是分佈在n維模式空間中的點xk。把屬於ω1的點比擬為某種能源點，在點上，電位達到峰值。隨著與該點距離的增大，電位分佈迅速減小，即把樣本xk附近空間x點上的電位分佈，看成是一個勢函式K(x, xk)。對於屬於ω1的樣本叢集，其附近空間會形成一個“高地”，這些樣本點所處的位置就是“山頭”。同理，用電位的幾何分佈來看待屬於ω2的模式樣本，在其附近空間就形成“凹地”。只要在兩類電位分佈之間選擇合適的等高線，就可以認為是模式分類的判別函式。
模式分類的判別函式可由分佈在模式空間中的許多樣本向量{xk, k=1,2,…且
從勢函式可以看出，積累位勢起著判別函式的作用，當xk+1屬於ω1時，Kk(xk+1)>0；當xk+1屬於ω2時，Kk(xk+1)<0，則積累位勢不做任何修改就可用作判別函式。由於一個模式樣本的錯誤分類可造成積累位勢在訓練時的變化，因此勢函式演算法提供了確定ω1和ω2兩類判別函式的迭代過程。判別函式表示式：取d(x)=K(x)，則有：dk+1(x)=
dk(x)+rk+1K(x, xk+1 )
判別函式產生逐步分析：
設初始勢函式K0(x) = 0
第一步：加入第一個訓練樣本x1，則有
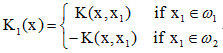這裡第一步積累勢函式K1(x)描述了加入第一個樣本時的邊界劃分。當樣本屬於ω1時，勢函式為正；當樣本屬於ω2時，勢函式為負。第二步：加入第二個訓練樣本x2，則有
（i）若
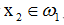且K1(x2)>0，或 且K1(x2)<0，則分類正確，此時K2(x) = K1(x)，即積累勢函式不變。（ii）若
且K1(x2)<0，則
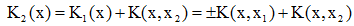（iii）若
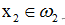且K1(x2)>0，則
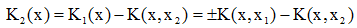以上（ii）、（iii）兩種情況屬於錯分。假如x2處於K1(x)定義的邊界的錯誤一側，則當
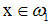時，積累位勢K2(x)要加K(x, x2)，當
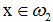時，積累位勢K2(x)要減K(x, x2)。第K步：設Kk(x)為加入訓練樣本x1，x2，…，xk後的積累位勢，則加入第(k+1)個樣本時，Kk+1(x)決定如下：
（i）若
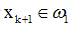且Kk(xk+1)>0，或 且Kk(xk+1)<0，則分類正確，此時Kk+1(x) = Kk(x)，即積累位勢不變。（ii）若
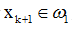且Kk(xk+1)<0，則
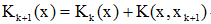（iii）若
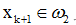且Kk(xk+1)>0，則
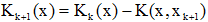因此，積累位勢的迭代運算可寫成：
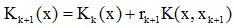，rk+1為校正係數：
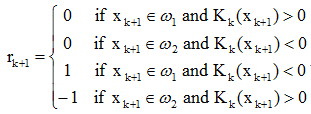若從給定的訓練樣本集{x1, x2, …, xk, …}中去除不使積累位勢發生變化的樣本，即使Kj(xj+1)>0且
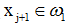，或Kj(xj+1)<0且
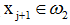的那些樣本，則可得一簡化的樣本序列
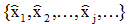，它們完全是校正錯誤的樣本。此時，上述迭代公式可歸納為：
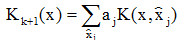其中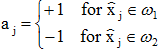
也就是說，由k+1個訓練樣本產生的積累位勢，等於ω1類和ω2類兩者中的校正錯誤樣本的總位勢之差。選擇勢函式的條件：一般來說，若兩個n維向量x和xk的函式K(x, xk)同時滿足下列三個條件，則可作為勢函式。K(x,
xk)= K(xk, x)，並且當且僅當x=xk時達到最大值；當向量x與xk的距離趨於無窮時，K(x, xk)趨於零；K(x, xk)是光滑函式，且是x與xk之間距離的單調下降函式。
構成勢函式的兩種方式：
第一類勢函式：可用對稱的有限多項式展開，即：
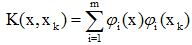
其中{
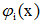}在模式定義域內為正交函式集。將這類勢函式代入判別函式，有：
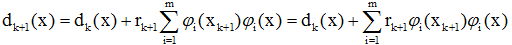
得迭代關係：
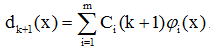其中：
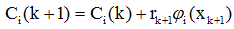
因此，積累位勢可寫成：
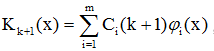，Ci可用迭代式求得。第二類勢函式：選擇雙變數x和xk的對稱函式作為勢函式，即K(x, xk) = K(xk, x)，並且它可展開成無窮級數，例如：
(a)
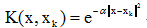
(b)
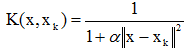，α是正常數
(c) 
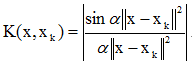
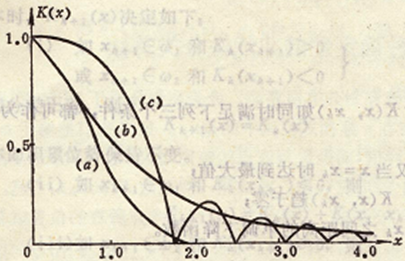用第二類勢函式，當訓練樣本維數和數目都較高時，需要計算和儲存的指數項較多。正因為勢函式由許多新項組成，因此有很強的
分類能力。