最小二乘法多項式曲線擬合原理與實現
阿新 • • 發佈:2019-02-13
程式碼:
# coding=utf-8 ''' 作者:Jairus Chan 程式:多項式曲線擬合演算法 ''' import matplotlib.pyplot as plt import math import numpy import random fig = plt.figure() ax = fig.add_subplot(111) #階數為9階 order=9 #生成曲線上的各個點 x = numpy.arange(-1,1,0.02) y = [((a*a-1)*(a*a-1)*(a*a-1)+0.5)*numpy.sin(a*2) for a in x] #ax.plot(x,y,color='r',linestyle='-',marker='') #,label="(a*a-1)*(a*a-1)*(a*a-1)+0.5" #生成的曲線上的各個點偏移一下,並放入到xa,ya中去 i=0 xa=[] ya=[] for xx in x: yy=y[i] d=float(random.randint(60,140))/100 #ax.plot([xx*d],[yy*d],color='m',linestyle='',marker='.') i+=1 xa.append(xx*d) ya.append(yy*d) '''for i in range(0,5): xx=float(random.randint(-100,100))/100 yy=float(random.randint(-60,60))/100 xa.append(xx) ya.append(yy)''' ax.plot(xa,ya,color='m',linestyle='',marker='.') #進行曲線擬合 matA=[] for i in range(0,order+1): matA1=[] for j in range(0,order+1): tx=0.0 for k in range(0,len(xa)): dx=1.0 for l in range(0,j+i): dx=dx*xa[k] tx+=dx matA1.append(tx) matA.append(matA1) #print(len(xa)) #print(matA[0][0]) matA=numpy.array(matA) matB=[] for i in range(0,order+1): ty=0.0 for k in range(0,len(xa)): dy=1.0 for l in range(0,i): dy=dy*xa[k] ty+=ya[k]*dy matB.append(ty) matB=numpy.array(matB) matAA=numpy.linalg.solve(matA,matB) #畫出擬合後的曲線 #print(matAA) xxa= numpy.arange(-1,1.06,0.01) yya=[] for i in range(0,len(xxa)): yy=0.0 for j in range(0,order+1): dy=1.0 for k in range(0,j): dy*=xxa[i] dy*=matAA[j] yy+=dy yya.append(yy) ax.plot(xxa,yya,color='g',linestyle='-',marker='') ax.legend() plt.show()
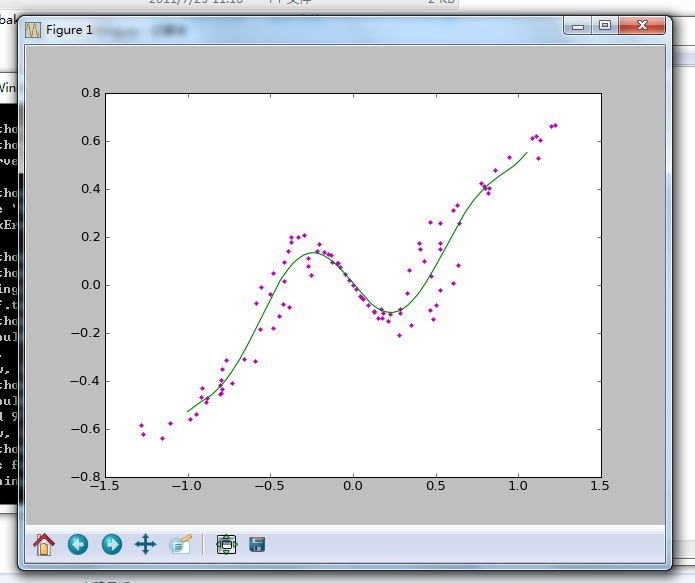
執行效果: