機器學習實戰(二)LR演算法:實現簡單的分類模型
阿新 • • 發佈:2019-02-13
說明:,裡面有更詳盡的Logistic Regression原理分析和案例實現流程詳解,是一個關於機器學習實戰的不錯的學習資料,推薦一波。出於程式設計實踐和機器學習演算法梳理的目的,按照自己的程式碼風格重寫該應用案例,在實現的過程中也很有助於自己的思考。為方便下次看時能快速理解便通過截圖的方式截取了個人認為比較關鍵的內容,推薦看原連結,自己在程式碼實現過程中會留下一些思考,也歡迎交流學習。
#更新# 剛發現之前整理的資料裡有個更完整的連結:邏輯迴歸梯度上升。
LR原理
這裡只擷取程式碼實現過程中關鍵的部分,即梯度上升公式,該截圖為最後一個參考連結裡面的,也是為了方便在程式碼中進行註釋,能夠更好地將程式碼實現和原理公式結合在一起看,加強理解。
LR演算法實現及分析
資料請到第一個參考連結裡面下載,這裡就不貼出來了。
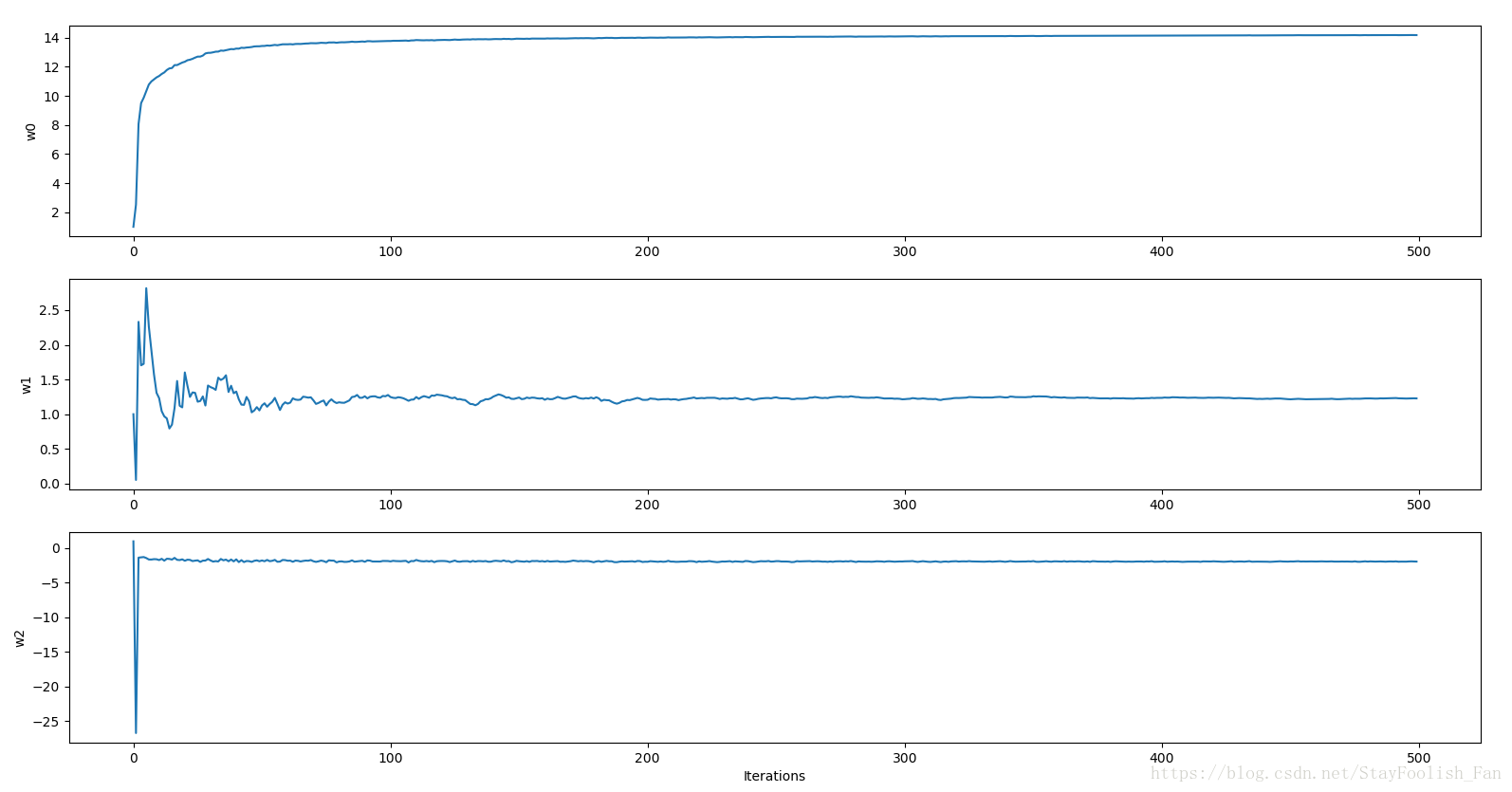
中間迭代訓練過程中[w1,w2,w3]的變化過程,200個迭代之後均趨於穩定。# __author__ = 'czx' # coding=utf-8 from numpy import * import matplotlib.pyplot as plt # 資料載入 def loadData(filename): f = open(filename) dataMat = [] labels = [] for line in f.readlines(): tempSample = line.strip().split('\t') dataMat.append([1.0,float(tempSample[0]),float(tempSample[1])]) labels.append(int(tempSample[2])) return dataMat,labels # Sigmoid啟用函式,這裡也給了tanh啟用函式 def sigmoid(X): return 1.0/(1+exp(-X)) #return 2*1.0/(1+exp(-2*X))-1 # tanh(x):mean value is 0 # 列印資料驗證資料載入是否正常 def dataCheck(): data,labels = loadData('datingTest.txt') print len(data),len(labels) for i in range(len(data)): print data[i],labels[i] # 用於顯示後面梯度上升訓練過程中的weights def trainingProcessDisplay(weights): fig = plt.figure() n = len(weights) x = range(n) ax1 = fig.add_subplot(311) ax1.plot(x,weights[:,0]) plt.ylabel('w0') ax = fig.add_subplot(312) ax.plot(x,weights[:,1]) plt.ylabel('w1') ax = fig.add_subplot(313) ax.plot(x,weights[:,2]) plt.ylabel('w2') plt.xlabel('Iterations') plt.show() # 梯度上升,每次更新都是計算出所有樣本之間的誤差(資料量很大時計算很耗時) def gradAscent(data,labels, alpha = 0.001, numIter=500): dataMatrix = mat(data) labelMat = mat(labels).transpose() m,n = shape(dataMatrix) weights = ones((n,1)) for k in range(numIter): h = sigmoid(dataMatrix*weights) # 啟用輸出 error = labelMat - h # 誤差計算,上圖中的藍色框公式 weights = weights + alpha*dataMatrix.transpose()*error # 權值更新,上圖中的紅色框公式 return array(weights) # 梯度上升,每次使用單個樣本進行更新,error為標量 def stocGradAscent0(data,labels, alpha = 0.001, numIter=500): m,n = shape(data) weights = ones(n) for j in range(numIter): for i in range(m): h = sigmoid(sum(data[i]*weights)) error = labels[i]-h weights = weights + alpha*error*data[i] return weights # 隨機梯度上升,每次迭代過程中順序不一樣,同樣也是單樣本更新 def stocGradAscent1(data,labels, numIter=500): m,n = shape(data) weights = ones(n) allWeights = ones((numIter,n)) for j in range(numIter): allWeights[j] = weights dataIndex = range(m) random.shuffle(dataIndex) for i in range(m): alpha = 4/(1.0+i+j) + 0.0001 index = dataIndex[i] h = sigmoid(sum(data[index]*weights)) error = labels[index] - h weights = weights + alpha *error*data[index] trainingProcessDisplay(allWeights) return weights # 結果視覺化:在這裡迴歸出來的是直線 def resultVisualization(data,labels,weights): n = shape(data)[0] x1 = [];y1=[];x2=[];y2=[] for i in range(n): if int(labels[i])==1: x1.append(data[i][1]);y1.append(data[i][2]) else: x2.append(data[i][1]);y2.append(data[i][2]) fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(x1,y1,s=30,c='red',marker='s') ax.scatter(x2,y2,s=30,c='green') x = arange(-5.0,5.0,0.1) # div = weights[2] # if weights[2]==0: div = 0.00001 y = (-weights[0]-weights[1]*x)/weights[2] ax.plot(x,y) plt.xlabel('X1');plt.ylabel('X2') plt.show() # 測試:其實也就只是將回歸直線繪製出來,真正測試的話應該要拿出一個測試集,然後計算測試誤差,以及後續對新樣本預測並作出相應的決策,這裡只做簡單分類就不介紹決策 def testLR(): data,labels = loadData("data.txt") dataArr = array(data) #weights = gradAscent(dataArr,labels) #weights = stocGradAscent0(dataArr,labels) weights = stocGradAscent1(dataArr,labels) #print weights resultVisualization(dataArr,labels,weights) # 主函式 if __name__ == "__main__": print 'hello LR !' # dataCheck() testLR()
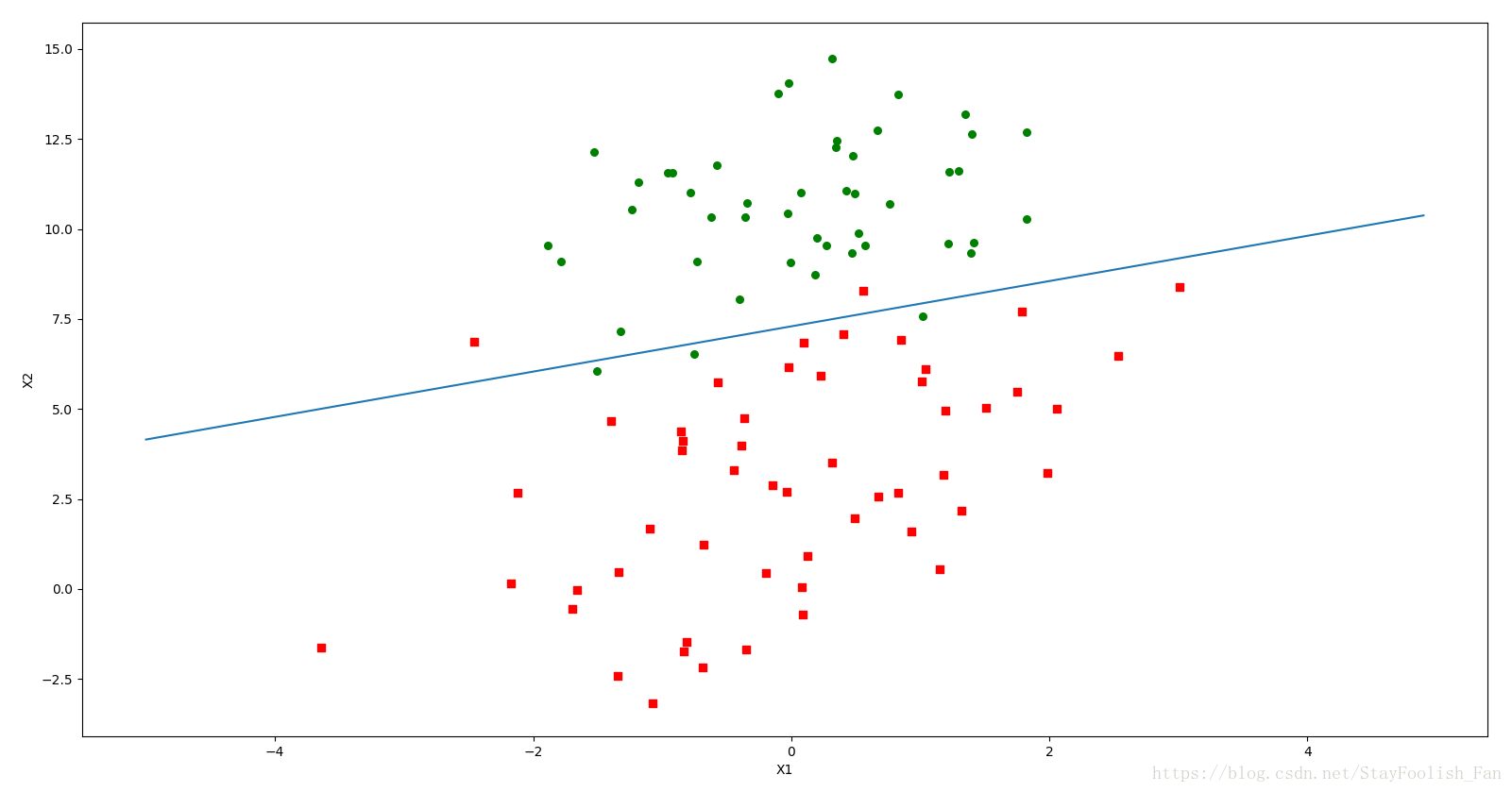
最後的模型視覺化。
小結
多寫程式碼
多寫程式碼
多寫程式碼