機器學習筆記(二)——廣泛應用於資料降維的PCA演算法實戰
最近在學習的過程當中,經常遇到PCA降維,於是就學習了PCA降維的原理,並用網上下載的iris.txt資料集進行PCA降維的實踐。為了方便以後翻閱,特此記錄下來。本文首先將介紹PCA降維的原理,然後進入實戰,編寫程式對iris.資料集進行降維。
一、為什麼要進行資料降維?
在資料處理中,經常會遇到特徵維度比樣本數量多得多的情況,如果直接放到機器學習演算法中,效果不一定好。一是因為冗餘的特徵會帶來一些噪音,影響計算的結果;二是因為無關的特徵會加大計算量,耗費時間和資源。因此,降維往往作為預處理步驟,在資料應用到其他演算法之前清洗資料。降維技術使得資料變得更易使用,並且它們往往能夠去除資料中的噪聲,使得其他機器學習任務更加精確。準確來說,
(1)降維可以緩解維數災難問題。
現實應用中屬性維數經常成千上萬,由於許多學習方法都涉及距離計算,而高維空間會給距離計算帶來很大的麻煩,例如當維數很高時甚至連計算內積都不再容易。通常,在高維情形下出現的資料樣本稀疏、距離計算困難等問題,是所有機器學習方法共同面臨的嚴重障礙,被稱為“維數災難”。緩解維數災難的一個重要途徑就是降維,亦稱為“維數約簡”,即通過某種數學變換將原始高維屬性空間轉變為一個低維“子空間”,在這個子空間中樣本密度大幅提高,距離計算也變得更為容易。
(2)降維可以在壓縮資料的同時讓資訊損失最小化。
我們希望在儘可能減少資訊損失的情況下來降低資料的維度
(3)由於人類思維的限制,理解幾百個維度的資料結構很困難,若將資料維數降至二維或三維,則可以通過視覺化技術來直觀地展示資料分佈。
二、PCA降維的概念
PCA是一種較為常用的降維技術,PCA的思想是將n維特徵對映到k維上,這k維是全新的正交特徵。在PCA中,資料從原來的座標系轉換到了新的座標系,新的座標系的選擇是由資料本身決定的。第一個新座標軸選擇的是原始資料中方差最大的方向,第二個新座標軸的選擇和第一個座標軸正交且具有最大方差的方向。該過程一直重複,重複次數為原始資料中特徵的數目。我們會發現,大部分方差都包含在最前面的幾個新座標軸中。因此,我們可以忽略餘下的座標軸,即對資料進行了降維處理。
三、PCA演算法的步驟
將資料轉換成前N個主成分的虛擬碼大致如下:
去除平均值
計算協方差矩陣
計算協方差矩陣的特徵值和特徵向量
將特徵值從大到小排序
保留最前面的N個特徵值所對應的特徵向量
將原始資料轉換到上述N個特徵向量構建的新空間中
具體的演算法流程如下所示:
四、PCA程式碼實現
本文基於iris資料集來進行PCA降維演示,Iris資料集是常用的分類實驗資料集,由Fisher, 1936收集整理。Iris也稱鳶尾花卉資料集,是一類多重變數分析的資料集。資料集包含150個數據集,分為3類,每類50個數據。其中每行資料包含每個樣本的四個特徵和樣本的類別資訊,可通過花萼長度,花萼寬度,花瓣長度,花瓣寬度4個屬性預測鳶尾花卉屬於(Setosa,Versicolour,Virginica)三個種類中的哪一類。所以Iris資料集是一個150行5列的二維表。
我們把樣本資料儲存在一個irisdata.txt的檔案當中,區域性樣本資料如下圖所示:
為了方便,本文的例子是想把二維的空間降成一維的空間,因此截取了花瓣長度和花瓣寬度這兩列資料作為樣本集(150*2),部分樣本集如下所示:
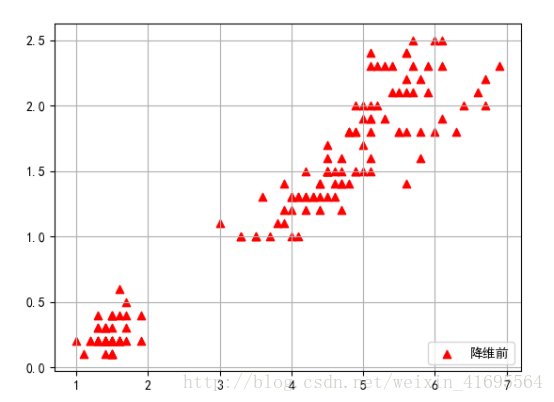
為了更加直觀的表示樣本資料集,我們利用matplotlib這個第三方繪相簿,採用散點圖的形式將資料展示出來,散點圖分佈如下所示:
接下編寫PCA演算法的程式碼,我們在irisdata.txt檔案所在的目錄下,新建了一個pca.py的檔案,並在裡面寫入以下程式碼,如下所示:
import numpy
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['simHei']
#這句話用來設定 matplotlib.pyplot模組繪製的圖中正常顯示中文字型
###################################
####PCA降維技術應用於iris資料集#####
#### time:2018.3.8 ####
#################################
def loaddataset(filename):
"""
這是一個載入iris資料集的函式
輸入: filename是iris資料集的相對儲存路徑
輸出: dataset是資料集合
"""
with open(filename) as fr:
rowArr = [line.strip().split(',')[2:] for line in fr.readlines()[1:]]
dataset =[]
for i in range(len(rowArr )):
dataArr = []
for j in range(2):
dataArr.append( float(rowArr[i][j] ))
dataset.append(dataArr )
return numpy.array(dataset)
def pcaProcessingData( dataset, figureNumber ):
"""
此函式的作用是對輸入的資料進行PCA降維處理
輸入: dataset是輸入的待處理的資料集
figureNumber用以指定降維後的資料維度
輸出:
"""
meanValue = numpy.mean( dataset,axis=0 ) #mean()函式對陣列進行求均值運算,其中axis=0表示對各列求均值,返回1* n陣列
centered_dataset = dataset - meanValue #將樣本資料進行中心化,即對每個維度減去這個維度的資料均值
covariance_matrix = numpy.cov( centered_dataset,rowvar=0 )
#cov()函式實現的是求出兩個變數的協方差矩陣,得到一個2*2的陣列,其中rowvar=0表示將每一列看作一個變數
eigenvalue,eigenvector = numpy.linalg.eig( covariance_matrix )
#eig()函式求解矩陣的特徵值和特徵向量,該函式將返回一個元組,其中第一個元素為特徵值,
# 第二個元素為特徵向量(且每一列為一個特徵向量)
eigenvalue_sorted_index = numpy.argsort( -eigenvalue )
#將特徵值陣列元素從大到小進行排序,並返回排序後元素的索引
projection_matrix = eigenvector[:,eigenvalue_sorted_index[:figureNumber]]
#取排序後的前figureNumber個特徵值所對應的特徵向量組成投影矩陣
newDataSet = numpy.dot(centered_dataset,projection_matrix) #得到原樣本向量在新座標系中的座標向量,即降維後的資料集
reconstructedData = numpy.dot ( newDataSet, projection_matrix.T ) + meanValue #將降維後的資料進行重構
return newDataSet, reconstructedData
def data_visualization( dataset, recondataset ):
"""
這是一個將資料集進行視覺化的函式,以散點圖的形式將資料展示出來
輸入: dataset是輸入的資料集
輸出: 散點圖
"""
x_coordinates_Arr1 = dataset[:,0]
y_coordinates_Arr1 = dataset[:,1]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(x_coordinates_Arr1, y_coordinates_Arr1, c='red',alpha=1,marker='^',label = u'降維前')
x_coordinates_Arr2 = recondataset[:, 0]
y_coordinates_Arr2 = recondataset[:, 1]
ax.scatter(x_coordinates_Arr2, y_coordinates_Arr2, c='green', alpha=1,marker='+',label =u'降維後')
plt.grid(True)
plt.legend(loc=4)
plt.show()
if __name__ == '__main__':
dataset = loaddataset('irisdata.txt')
print(dataset)
newDataSet, reconstructedData = pcaProcessingData(dataset, 1)
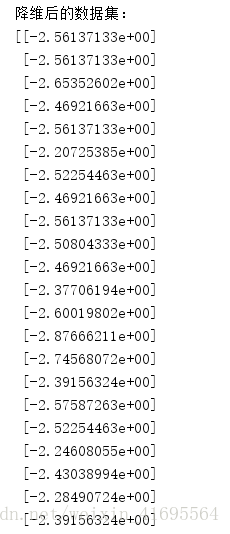
print('降維後的資料集:')
print(newDataSet)
data_visualization( dataset,reconstructedData )
執行上述程式碼,得到結果如下所示:
降維後的資料集(區域性):
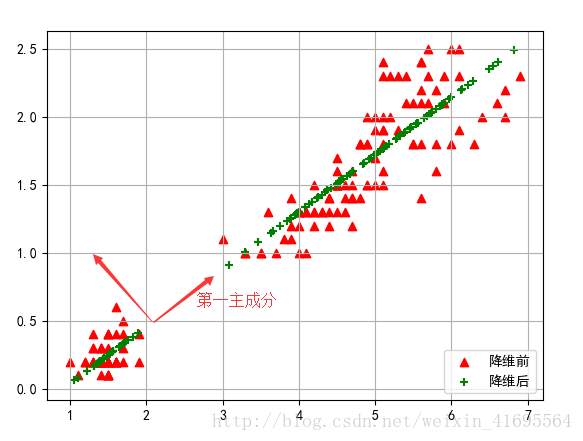
得到原始資料集(紅色三角形點表示)及第一主成分(綠色叉號表示),如下:
參考資料:
[1] 周志華 《機器學習》
[2] Peter Harrington 《機器學習實戰》