上一篇介紹了自定義view需要知道的基本函式。新開一篇獻給借給我vpn的深圳_奮鬥小哥。

轉載請註明出處：http://blog.csdn.net/wingichoy/article/details/50492828

今天給大家介紹一個非常神奇的曲線，貝塞爾曲線。相信大家之前都有耳聞。

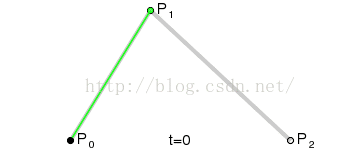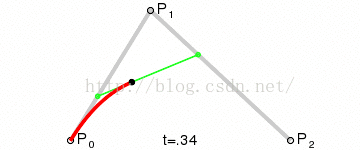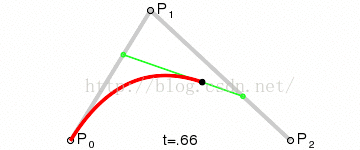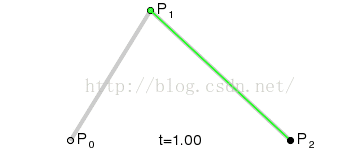
很久之前就久聞該線大名，但是一直不是很瞭解，在經過一番谷歌之後，有了初步的概念：三點確定一條曲線：起點，終點，輔助點。

三個點的基本關係如下：

當初看這圖我也看了老半天，只知道是非常平滑，不知道三個點的具體關係，於是變寫了一段程式來測試輔助點與始終點的關係。

Android 的Path類提供了繪製二階貝塞爾曲線的方法，使用方法如下：

        //設定起點
        path.moveTo(200,200);
        //設定輔助點座標 300，200       終點座標400，200

        path.quadTo(300, 200, 400, 200);

這裡我將貝塞爾曲線的輔助點y軸和起始點設定相同，draw以後效果如下：

看到是一條直線，這是因為他y軸沒有拉伸，只是x軸進行了拉伸。把輔助點y+100嘗試

看到已經拉伸。。其實這樣還是不能很好的體現 貝塞爾曲線的規律。 所以要持續改變，研究他的規律，這裡重寫onTouchEvent，讓觸控點的位置作為輔助點。觀察變化。

@Override
    protected void onDraw(Canvas canvas) {
        Paint p = new Paint();
        p.setStyle(Paint.Style.STROKE);
        p.setStrokeWidth(10);
        Path path = new Path();
        path.moveTo(200, 200);
        path.quadTo(mSupX, mSupY, 400, 200);
        canvas.drawPath(path,p);
        super.onDraw(canvas);
    }

    @Override
    public boolean onTouchEvent(MotionEvent event) {
        switch (event.getAction()){
            case MotionEvent.ACTION_MOVE:
                mSupX = event.getX();
                mSupY = event.getY();
                invalidate();
        }
        return true;
    }
 

可以看到 是根據滑鼠位置變化的曲線，可是現在還是不能很好的表現曲線的突出點和輔助點關係，接下來把輔助點也畫出來，方便觀察。

        canvas.drawPoint(mSupX,mSupY,p);

這下，輔助點和曲線的關係就很明顯了。

許多炫酷的效果都離不開貝塞爾曲線，貝塞爾曲線的應用：仿360記憶體清理效果。