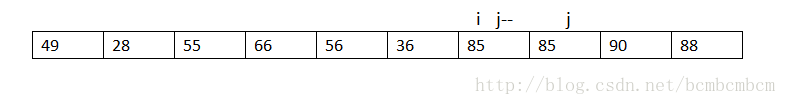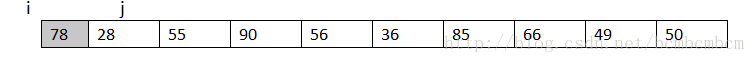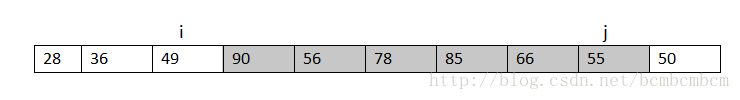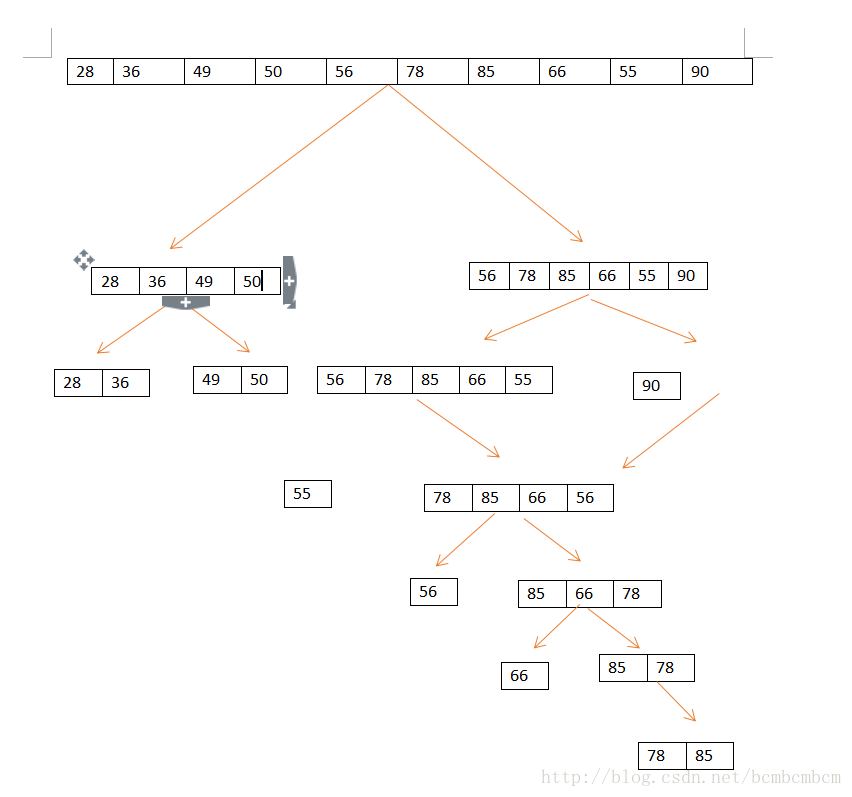
首先快速排序是C.R.A.Hoare於1962年提出的一種劃分交換排序。它採用了一種分治的策略，通常稱其為分治法(Divide-and-ConquerMethod)。

方法一：

該方法的基本思想是：
1．先從數列中指定一個數作為基準數。
2．進行分割槽，將比這個數大的數全放到它的右邊，小於或等於它的數全放到它的左邊。
3．再對左右區間重複第二步，直到各區間只有一個數。
設定一個數據源陣列dataSource

設定第一個數為中間數，大於此數的放在其右邊，小於等於此數的放在其左邊。
大致思路是：
首先，我先用一個變數來儲存中間數的值及78；

然後設定陣列的firstindex為i，lastindex為j，從陣列的最後向前遍歷，如果發現有小於78的，就使s[i]=s[j],及s[1]=49
 

陣列值改變後，i++;
找到一個小於中間數的值後，再從前往後找大於中間數的值，

找到90大於78，然後讓s[j]=90，j--(把這個坑填上，但是前面又有多出一個坑即s[i])    

然後再從後往前找小於78的數，66<78，再賦值，即s[i]=66，i++

再從前往後找大於78的數，85>78,賦值s[j]=85,j--

此刻，i=j,不符合i<j這個條件，跳出迴圈遍歷即可，但是此時數組裡的 還有一個坑沒有填上，即s[i],那麼這是就可以把中間數放到這裡即可

此時，小於78的放在了前面，大於78的就被放到了後面，在index i 這分成了兩部分，按照上面的步驟，分別對這兩部分進行操作即可。
下面上程式碼：
 

 //正向想   --- 程式碼有些囉嗦
   private int[] dataArray = {75,8,55,90,56,36,85,77,49,88};

    public void quicksort(int[] s,int left,int right){
        if (left < right) {
            int i = left, j = right;
            //去第一個數為中間數
            int x = s[left];
            //從後往前找小於 中間數的值，把其放在i的位置
            while
 
 (i < j) {
                while (i < j) {
                    if (s[j] < x) {
                        s[i] = s[j];
                        i++;
                        break;
                    }
                    j--;
                }

                //從前向後找大於中間數的值，把其放在j的位置
                while (i < j) {
                    if (s[i] > x) {
                        s[j] = s[i];
                        j--;
                        break;
                    }
                    i++;
                }
            }
            s[i] = x;
            quicksort(s, left, i - 1);
            quicksort(s, i + 1, right);
        }
    }
    //反向想   --- 簡化版
    void quick_sort(int s[], int left, int right)
    {
        if (left < right) {
            //第一個數為中間數
            int i = left, j = right, x = s[left];
            while (i < j)
            {
                while(i < j && s[j] >= x) // 從右向左找第一個小於x的數
                    j--;
                if(i < j)
                    //從後往前找小於 中間數的值，把其放在i的位置，然後i+1
                    s[i++] = s[j];

                while(i < j && s[i] < x) // 從左向右找第一個大於等於x的數
                    i++;
                if(i < j)
                    //從前向後找大於中間數的值，把其放在j的位置,然後 j-1
                    s[j--] = s[i];
            }
            s[i] = x;
            quick_sort(s, left, i - 1); // 遞迴呼叫
            quick_sort(s, i + 1, right);
        }
    }

  @Test
    public void testSort(){

        quicksort(dataArray,0,dataArray.length-1);

        for (int k = 0;k<dataArray.length;k++){
            System.out.println(dataArray[k]);
        }
    }

方法二：

找到符合的就交換  而不是把中間數記錄下來
設定陣列的最後一個數是中間數。
i = (firstIndex)left - 1;
j = (firstIndex)left

s[i]=78>50,不交換，j++；

28<50,i++,交換，j++,

55>50,不交換，j++;

90>50,不交換，j++;

56>50,不交換,j++

36<50,i++，交換，j++;

此時，小於50的放在了前面，大於50的就被放到了後面，在index i 這分成了兩部分，按照上面的步驟，分別對這兩部分進行操作即可。
下面上程式碼

 // 交換版 ---  找到符合的就交換  而不是把中間數記錄下來
    public  void swap(int s[],int i,int j){
        int temp;
        temp = s[i];
        s[i] = s[j];
        s[j] = temp;
    }

    public void quick__sork(int s[], int left, int right){
        if (left < right) {
            //最後一個數為中間數
            int i = left-1, j = left;
            //i是最後一個小於中間數的值
            //一進迴圈，先使 i+1                                                                                  
            //使i 一直是 第一個大於中間數 的值，只要找到小於中間數的，就和s[i]交換
            while (j<=right) {
                if (s[j]<=s[right]){
                    i++;
                    swap(s,i,j);
                }
                j++;
            }
            quick__sork(s,left,i-1);
            quick__sork(s,i+1,right);
        }

    }

三、時間複雜度

快速排序的最好情況：O(nlog n),最壞情況：O(n^2)
最好情況：每次都恰好五五分，一次遞迴共需比較n次，遞迴深度為log n
最壞情況：已排序陣列，比較次數為n-1+n-2+...+1=n*(n-1)/2 ~1*n^2/2