今天，來講一講合併排序，其實我已經寫了 堆排序 和 快速排序，本來都不想寫這個，但是，當我發現我身邊很多人竟然都不知道這個排序的時候，我震驚了，畢竟，這是一個經典的入門演算法（反正外國貌似是這樣的，根據我看的書和視訊），歷史也十分悠久。下面就來講講這歷史悠久的演算法。

        合併排序是一種典型的分治法演算法。先把陣列拆成兩個陣列，對兩個陣列進行繼續拆分，直到能夠對拆分後的兩個結果分別進行排序。也就是說，拆分後，使兩邊都是排好序的。顯然當拆分到兩邊只剩下一個的時候，自然就是有序的。

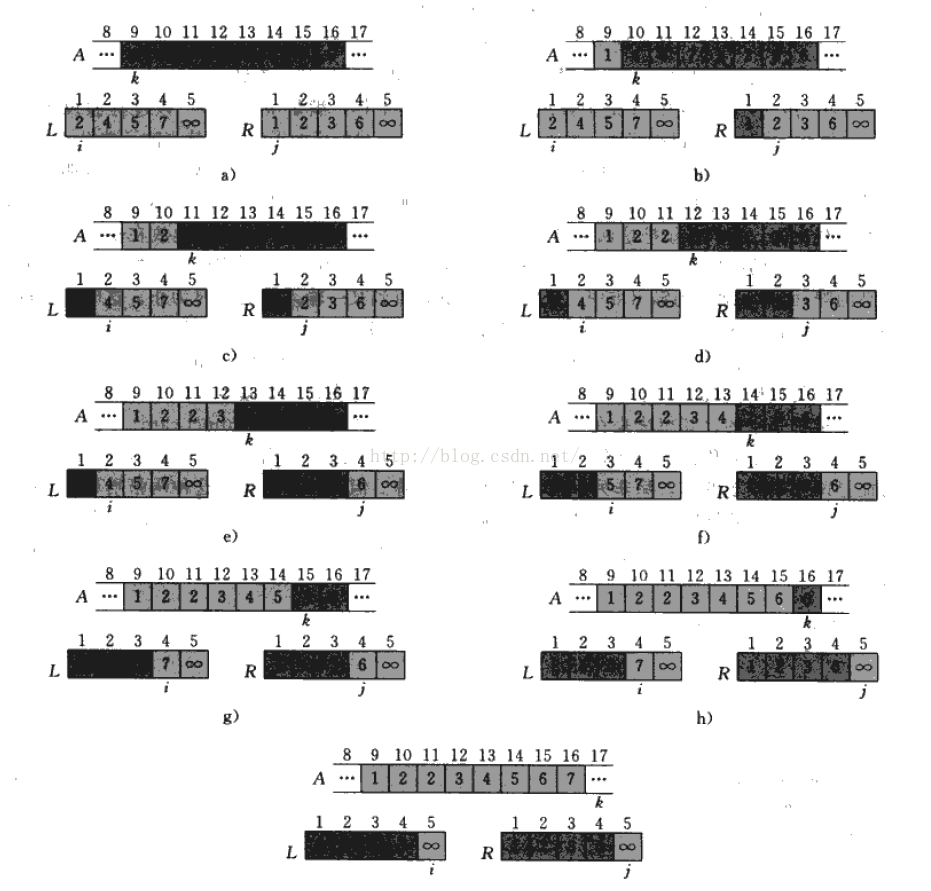
        拆分過後是合併，合併也是這個演算法的核心過程，其實就好比是兩副牌，這兩副牌已經是有序的，要把它們合併，只要每次都翻開最上面一張牌，然後進行對比，把小的（或此處按照遞增排序舉例）拿走。然後繼續翻牌。很顯然，這裡會用到額外的陣列空間，所以合併排序並不是原地排序。為了簡化這個過程，合併的時候，在兩副牌下面都放置一個無窮大的哨兵牌。具體過程如下圖所示。

本圖選自演算法導論。實現程式碼如下：

    /**合併排序演算法，一個數字的時候算已排序。最後合併排序過的陣列
     * @param A
     * @param p
     * @param r
     */
    public void MergeSort(int[] A, int p, int r){
        if(p < r){
            int q = (p + r) / 2;
            MergeSort(A, p, q);
            MergeSort(A, q+1, r);
            Merge(A, p, q, r);
        }
    }
 

    /**合併排序過的陣列，把陣列分成了[p --> q],[q+1 --> r]
     * @param A 陣列A
     * @param p
     * @param q
     * @param r
     * @return
     */
    public int[] Merge(int[] A, int p, int q, int r){
        int n1 = q - p + 1;
        int n2 = r - q;
        int[] L = new int[n1 + 1];
        int[] R = new int[n2 + 1];
        for(int i = 0; i < n1; i++){
            L[i] = A[p + i];
        }
        for(int i = 0; i < n2; i++){
            R[i] = A[q + i + 1];
        }
        L[n1] = Integer.MAX_VALUE;
        R[n2] = Integer.MAX_VALUE;
        int i = 0, j = 0;
        for(int k = p; k <= r; k++){
            if(L[i] <= R[j]){
                A[k] = L[i];
                i++;
            }else{
                A[k] = R[j];
                j++;
            }
        }
        return A;
    }
 

如果發現問題，請立刻告訴我。我可不想誤人子弟