1.多層前饋神經網路
首先說下多層前饋神經網路，BP演算法，BP神經網路之間的關係。多層前饋（multilayer feed-forward）神經網路由一個輸入層、一個或多個隱藏層和一個輸出層組成，後向傳播(BP)演算法在多層前饋神經網路上面進行學習，採用BP演算法的（多層）前饋神經網路被稱為BP神經網路。給出一個多層前饋神經網路的拓撲結構，如下所示：

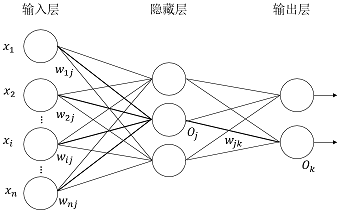
圖1 多層前饋神經網路

神經網路的拓撲結構包括：輸入層的單元數、隱藏層數(如果多於一層)、每個隱藏層的單元數和輸出層的單元數。神經網路可以用於分類（預測給定元組的類標號）和數值預測（預測連續值輸出）等。


2.後向傳播（BP）演算法詳解
（1）初始值權重
神經網路的權重被初始化為小隨機數，每個神經元都有一個相關聯的偏置，同樣也被初始化為小隨機數。
（2）前向傳播輸入
以單個神經網路單元為例，如下所示：

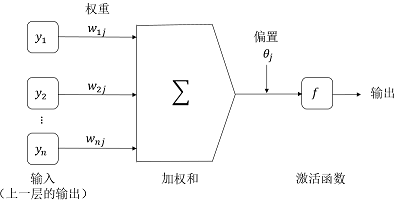
圖2 神經網路單元

給定隱藏層或輸出層的單元j$j$，到單元j$j$的淨輸入Ij$I_j$，如下所示：

Ij=∑iwijOi+θj$$I_j=\sum _i{w}_{ij}{O}_i+{\theta }_j$$
其中，wij$w_{ij}$是由上一層的單元i$i$到單元j$j$的連線的權重；Oi$O_i$是上一層的單元i$i$的輸出；θj${\theta }_j$是單元j$j$的偏置。需要說明的是偏置充當閥值，用來改變單元的活性。
給定單元j$j$的淨輸入Ij$I_j$，單元j$j$的輸出Oj$O_j$，如下所示：
Oj=11+e−Ij$$O_j=\frac{1}{1+e^{-I_j}}$$
（3）後向傳播誤差

1. 對於輸出層單元j$j$，誤差Errj$Er{r}_j$用下式計算：
   Errj=Oj(1−Oj)(Tj−Oj)$$Er{r}_j=O_j\left(1-O_j\right)(T_j-O_j$$
   )
   其中，Oj$O_j$是單元j$j$的實際輸出，而Tj$T_j$是j$j$給定訓練元組的已知目標值。需要說明的是，Oj(1−Oj)$O_j\left(1-O_j\right)$是邏輯斯締函式的導數。
2. 對於隱藏層單元j$j$，它的誤差用下式計算：
   Errj=Oj(1−Oj)∑kErrkwjk$$Er{r}_j=O_j\left(1-O_j\right)\sum _{k}Er{r}_k{w}_{jk}$$
   其中，wjk$w_{jk}$是由下一較高層中單元k$k$到單元j$j$的連線權重，而Errj$Er{r}_j$是單元k$k$的誤差。
3. 權重更新，如下所示：
   Δwij=(l)Errj

   相關推薦

   多層前饋神經網路及BP演算法

   1.多層前饋神經網路 首先說下多層前饋神經網路，BP演算法，BP神經網路之間的關係。多層前饋（multilayer feed-forward）神經網路由一個輸入層、一個或多個隱藏層和一個輸出層組成，後向傳播(BP)演算法在多層前饋神經網路上面進行學習，採用BP

   多層前饋神經網路的後向傳播演算法推導

   神經網路模型定義 本文研究的多層前饋神經網路（Multi-layer Feedforward Neural Networks），包含多層神經元，每層神經元與下一層神經元完全連線，神經元之間不存在同層連線，也不存在跨層連線. 設神經網路的層數為 N, 其中包括

   python實現多層前饋神經網路（手寫體識別）

   前饋神經網路的圖例及推導過程見https://blog.csdn.net/u010089444/article/details/52555567，接下來我們用python語言實現多層前饋神經網路。本例使用的是MINST資料集，由輸入層,兩個隱藏層,輸出層. MNIST資料集中

   深度學習-多層前饋神經網路

   因為公式都是在mathtype上寫的，然後插入到ppt的，而且裡面有很多圖，再用MD寫一遍簡直太耗時間，所以我就直接當作圖片插入發部落格了，還請讀者諒解。本來ppt是我們每週開組會用的，相互講解交流，自己做這些也廢了不少時間心血，覺得還可以，所以就和大家分享出來

   機器學習：神經網路-多層前饋神經網路淺析（附程式碼實現）

   M-P神經元模型神經網路中最基本的組成成分：神經元模型。如下圖是一個典型的“M-P神經元模型”：上圖中，神經元接收到n個其他神經元傳遞過來的輸入訊號，這些訊號通過權重的連線進行傳遞，神經元接收到的總輸入值與神經元的閾值進行比較，並通過“啟用函式”處理產生神經元輸出。常用S函式

   前饋神經網路，BP演算法

   單層感知機輸入層——>輸出層啟用函式在輸出層，常見啟用函式Logistic、softmax函式多層感知機（MLP）輸入層——>隱藏層——>輸出層啟用函式在隱藏層，線性變換預啟用+非線性啟用函式，資料分佈“線性可分”隱藏層所含神經元越多，可提取特徵越多常用啟用

   單隱層前饋神經網路

   這篇部落格主要介紹神經網路基礎，單隱層前饋神經網路與反向傳播演算法。 神經網路故名思議是由人的神經系統啟發而得來的一種模型。神經網路可以用來做分類和迴歸等任務，其具有很好的非線性擬合能力。接下來我們就來詳細介紹一下但隱層前饋神經網路。 首先我們來看一下神經元的數學模型，如下圖所示：

   多層前饋神經元網路

   做了一個神經元網路分類器。開始步長設定為迭代次數的倒數，效果不好；後來調整到 0.2 效果比較好。測試一個拋物線邊界的例子，準確率大約 96% 以上。 public final class NeuroNetwork { private static class Neu

   前向神經網路和 BP 演算法詳解 --- 之 DNN

   前向神經網路和 BP 演算法詳解 一、神經網路的概念詳解 1.1、人工神經網路的基礎單元 — > 感知機 1.1.1、感知機模型講解 首先我們需要明確一點就是，針對於擁有核函式的 SVM 或者多隱層 + 啟用函式的多層神

   CNTK API文件翻譯(3)——前饋神經網路

   這個教程的目的是為了讓你熟悉使用CNTK元件來進行分類任務，如果你看了本系列的邏輯迴歸部分或者熟悉機器學習，可以跳過介紹部分。 介紹（見上期，本期略） 前饋神經網路模型 本次使用的資料集和上期邏輯迴歸教程使用的資料集一樣，不過這期的模型會結合多個邏

   【機器學習】神經網路及BP推導

   1 前向傳播 這裡的推導都用矩陣和向量的形式，計算單個變數寫起來太麻煩。矩陣、向量求導可參見上面參考的部落格，個人覺得解釋得很直接很好。 前向傳播每一層的計算如下： z(l+1)=W(l,l+1)a(l)+b(l,l+1)(1.1) a(l+

   深度學習：前饋神經網路

   神經元模型，由兩部分組成。一部分將訊號進行累加，得到得分函式，還有偏置項（bias），相當於函式的截距項或者常數項。 Z=bias+∑i=1mxiwi=∑i=0mxiwiZ=bias+∑i=1mxi

   TensorFlow官方教程學習筆記（五）——前饋神經網路

   本文主要是在TensorFlow上搭建一個前饋神經網路（feed-forward neural network）來對TensorFlow的運作方式進行簡單介紹。 程式碼在\examples\tutorials\mnist\中，主要使用兩個檔案：mnist.py和fully

   構建多層感知器神經網路對數字圖片進行文字識別

   在Keras環境下構建多層感知器模型，對數字影象進行精確識別。 模型不消耗大量計算資源，使用了cpu版本的keras，以Tensorflow 作為backended，在ipython互動環境jupyter notebook中進行編寫。 1.資料來源 此資料庫包含四部分：訓練資

   前饋神經網路（matlab例項）

   定義回顧 前饋網路也稱前向網路。這種網路只在訓練過程會有反饋訊號，而在分類過程中資料只能向前傳送，直到到達輸出層，層間沒有向後的反饋訊號，因此被稱為前饋網路。感知機( perceptron)與BP神經網路就屬於前饋網路。 對於一個3層的前饋神經網路N，若用X

   keras中使用MLP(多層感知機)神經網路來實現MNIST手寫體識別

       Keras是一個基於python的的深度學習框架，比tensorflow更簡單易用，適合入門學習，本篇文章主要介紹使用keras實現手寫體識別任務。環境為python3+，Keras2.1，神經網路基礎知識在此不做過多介紹。    1.    載入MNIST資料。方式

   前饋神經網路的權值初始化方法

   前饋神經網路（Feedforward Neural Networks, FNNs）在眾多學習問題，例如特徵選擇、函式逼近、以及多標籤學習中有著不錯的應用。 針對訓練前饋網路的學習演算法，目前已經有不少研究者提出了新穎的研究結果，但是其它相關問題的研究卻不多，例

   Pybrain學習筆記-4 基於前饋神經網路的分類器

   話不多說，直接上程式碼： 5.test_pybrian_5 #!usr/bin/env python #_*_coding:utf-8_*_ ''' Created on 2017年4月14日 Topic：Classification with Feed-Forward Neural Networks @a

   一文理清深度學習前饋神經網路

   深度學習之文字分類模型-前饋神經網路(Feed-Forward Neural Networks)

   目錄DAN(Deep Average Network)Fasttextfasttext文字分類fasttext的n-gram模型Doc2vec DAN(Deep Average Network) MLP（Multi-Layer Perceptrons）叫做多層感知機，即由多層網路簡單堆疊而成，進而我們可以在輸