1. 引言

上一節我們講完了各種激勵函式的優缺點和選擇，以及網路的大小以及正則化對神經網路的影響。這一節我們講一講輸入資料預處理、正則化以及損失函式設定的一些事情。

2. 資料與網路的設定

前一節提到前向計算涉及到的元件(主要是神經元)設定。神經網路結構和引數設定完畢之後，我們就得到得分函式/score function(忘記的同學們可以翻看一下之前的博文)，總體說來，一個完整的神經網路就是在不斷地進行線性對映(權重和input的內積)和非線性對映(部分激勵函式作用)的過程。這一節我們會展開來講講資料預處理，權重初始化和損失函式的事情。

2.1 資料預處理

在卷積神經網處理影象問題的時候，影象資料有3種常見的預處理可能會用到，如下。我們假定資料表示成矩陣為X

，其中我們假定X是[N*D]維矩陣(N是樣本資料量，D為單張圖片的資料向量長度)。

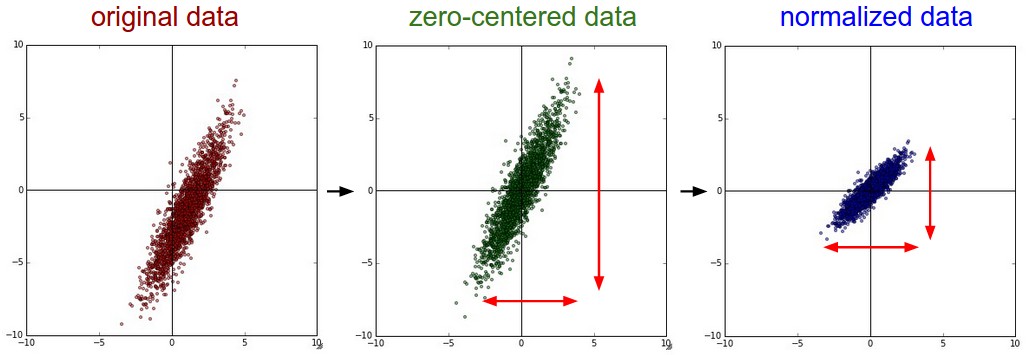
• 去均值，這是最常見的圖片資料預處理，簡單說來，它做的事情就是，對待訓練的每一張圖片的特徵，都減去全部訓練集圖片的特徵均值，這麼做的直觀意義就是，我們把輸入資料各個維度的資料都中心化到0了。使用python的numpy工具包，這一步可以用X -= np.mean(X, axis = 0)輕鬆實現。當然，其實這裡也有不同的做法：簡單一點，我們可以直接求出所有畫素的均值，然後每個畫素點都減掉這個相同的值；稍微優化一下，我們在RGB三個顏色通道分別做這件事。
• 歸一化，歸一化的直觀理解含義是，我們做一些工作去保證所有的維度上資料都在一個變化幅度上。通常我們有兩種方法來實現歸一化。一個是在資料都去均值之後，每個維度上的資料都除以這個維度上資料的標準差(X /= np.std(X, axis = 0)
  )。另外一種方式是我們除以資料絕對值最大值，以保證所有的資料歸一化後都在-1到1之間。多說一句，其實在任何你覺得各維度幅度變化非常大的資料集上，你都可以考慮歸一化處理。不過對於影象而言，其實這一步反倒可做可不做，因為大家都知道，畫素的值變化區間都在[0,255]之間，所以其實影象輸入資料天生幅度就是一致的。

上述兩個操作對於資料的作用，畫成示意圖，如下： 

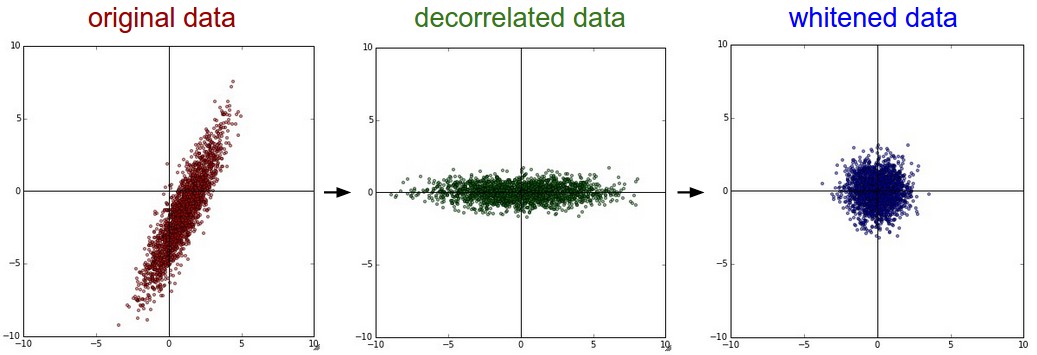
• PCA和白化/whitening，這是另外一種形式的資料預處理。在經過去均值操作之後，我們可以計算資料的協方差矩陣，從而可以知道資料各個維度之間的相關性，簡單示例程式碼如下：

# 假定輸入資料矩陣X是[N*D]維的
X -= np.mean(X, axis = 0
 
) # 去均值
cov = np.dot(X.T, X) / X.shape[0] # 計算協方差

得到的結果矩陣中元素(i,j)表示原始資料中，第i維和第j維之間的相關性。有意思的是，其實協方差矩陣的對角線包含了每個維度的變化幅度。另外，我們都知道協方差矩陣是對稱的，我們可以在其上做矩陣奇異值分解(SVD factorization)：

U,S,V = np.linalg.svd(cov)

其中U為特徵向量，我們如果相對原始資料(去均值之後)做去相關操作，只需要進行如下運算：

Xrot = np.dot(X, U)

這麼理解一下可能更好，U是一組正交基向量。所以我們可以看做把原始資料X投射到這組維度保持不變的正交基底上，從而也就完成了對原始資料的去相關。如果去相關之後你再求一下Xrot的協方差矩陣，你會發現這時候的協方差矩陣是一個對角矩陣了。而numpy中的np.linalg.svd更好的一個特性是，它返回的U是對特徵值排序過的，這也就意味著，我們可以用它進行降維操作。我們可以只取top的一些特徵向量，然後做和原始資料做矩陣乘法，這個時候既降維減少了計算量，同時又儲存下了絕大多數的原始資料資訊，這就是所謂的主成分分析/PCA：

Xrot_reduced = np.dot(X, U[:,:100])

這個操作之後，我們把原始資料集矩陣從[N*D]降維到[N*100]，儲存了前100個能包含絕大多數資料資訊的維度。實際應用中，你在PCA降維之後的資料集上，做各種機器學習的訓練，在節省空間和時間的前提下，依舊能有很好的訓練準確度。

最後我們再提一下whitening操作。所謂whitening，就是把各個特徵軸上的資料除以對應特徵值，從而達到在每個特徵軸上都歸一化幅度的結果。whitening變換的幾何意義和理解是，如果輸入的資料是多變數高斯，那whitening之後的 資料是一個均值為0而不同方差的高斯矩陣。這一步簡單程式碼實現如下：

#白化資料
Xwhite = Xrot / np.sqrt(S + 1e-5)

提個醒：whitening操作會有嚴重化噪聲的可能。注意到我們在上述程式碼中，分母的部分加入了一個很小的數1e-5，以防止出現除以0的情況。但是資料中的噪聲部分可能會因whitening操作而變大，因為這個操作的本質是把輸入的每個維度都拉到差不多的幅度，那麼本不相關的有微弱幅度變化的噪聲維度，也被拉到了和其他維度同樣的幅度。當然，我們適當提高墳墓中的安全因子(1e-5)可以在一定程度上緩解這個問題。

下圖為原始資料到去相關到白化之後的資料分佈示意圖： 

我們來看看真實資料集上的操作與得到的結果，也許能對這些過程有更清晰一些的認識。大家都還記得CIFAR-10影象資料集吧。訓練集大小為50000*3072，也就是說，每張圖片都被展成一個3072維度的列向量了。然後我們對原始50000*3072資料矩陣做SVD分解，進行上述一些操作，再視覺化一下，得到的結果示意圖如下：

我們稍加解釋一下，最左邊是49張原始圖片；左起第2幅圖是最3072個特徵向量中最top的144個，這144個特徵向量包含了絕大多數資料變數資訊，而其實它們代表的是圖片中低頻的資訊；左起第3幅圖表示PCA降維操作之後的49張圖片，使用上面求得的144個特徵向量。我們可以觀察到圖片好像被蒙上了一層東西一樣，模糊化了，這也就表明了我們的top144個特徵向量捕捉到的都是影象的低頻資訊，不過我們發現影象的絕大多數資訊確實被保留下來了；最右圖是whitening的144個數通過乘以U.transpose()[:144,:]還原回圖片的樣子，有趣的是，我們發現，現在低頻資訊基本都被濾掉了，剩下一些高頻資訊被放大呈現。

實際工程中，因為這個部分講到資料預處理，我們就把基本的幾種資料預處理都講了一遍，但實際卷積神經網中，我們並沒有用到去相關和whitening操作。當然，去均值是非常非常重要的，而每個畫素維度的歸一化也是常用的操作。

特別說明，需要特別說明的一點是，上述的預處理操作，一定都是在訓練集上先預算的，然後應用在交叉驗證/測試集上的。舉個例子，有些同學會先把所有的圖片放一起，求均值，然後減掉均值，再把這份資料分作訓練集和測試集，這是不對的親！！！

2.2 權重初始化

我們之前已經看過一個完整的神經網路，是怎麼樣通過神經元和連線搭建起來的，以及如何對資料做預處理。在訓練神經網路之前，我們還有一個任務要做，那就是初始化引數。

錯誤的想法：全部初始化為0，有些同學說，那既然要訓練和收斂嘛，初始值就隨便設定，簡單一點就全設為0好了。親，這樣是絕對不行的！！！為啥呢？我們在神經網路訓練完成之前，是不可能預知神經網路最後的權重具體結果的，但是根據我們歸一化後的資料，我們可以假定，大概有半數左右的權重是正數，而另外的半數是負數。但設定全部初始權重都為0的結果是，網路中每個神經元都計算出一樣的結果，然後在反向傳播中有一樣的梯度結果，因此迭代之後的變化情況也都一樣，這意味著這個神經網路的權重沒有辦法差異化，也就沒有辦法學習到東西。

很小的隨機數，其實我們依舊希望初始的權重是較小的數，趨於0，但是就像我們剛剛討論過的一樣，不要真的是0。綜合上述想法，在實際場景中，我們通常會把初始權重設定為非常小的數字，然後正負儘量一半一半。這樣，初始的時候權重都是不一樣的很小隨機數，然後迭代過程中不會再出現迭代一致的情況。舉個例子，我們可能可以這樣初始化一個權重矩陣W=0.0001*np.random.randn(D,H)。這個初始化的過程，使得每個神經元的權重向量初始化為多維高斯中的隨機取樣向量，所以神經元的初始權重值指向空間中的隨機方向。

特別說明：其實不一定更小的初始值會比大值有更好的效果。我們這麼想，一個有著非常小的權重的神經網路在後向傳播過程中，回傳的梯度也是非常小的。這樣回傳的”訊號”流會相對也較弱，對於層數非常多的深度神經網路，這也是一個問題，回傳到最前的迭代梯度已經很小了。

方差歸一化，上面提到的建議有一個小問題，對於隨機初始化的神經元引數下的輸出，其分佈的方差隨著輸入的數量，會增長。我們實際上可以通過除以總輸入數目的平方根，歸一化每個神經元的輸出方差到1。也就是說，我們傾向於初始化神經元的權重向量為w = np.random.randn(n) / sqrt(n)，其中n為輸入數。

我們從數學的角度，簡單解釋一下，為什麼上述操作可以歸一化方差。考慮在激勵函式之前的權重w與輸入x的內積s=∑niwixi部分，我們計算一下s的方差：

Var(s)=Var(∑inwixi)=∑inVar(wixi)=∑in[E(wi)]2Var(xi)+E[(xi)]2Var(wi)+Var(xi)Var(wi)=∑inVar(xi)Var(wi)=(nVar(w))Var(x)

注意，這個推導的前2步用到了方差的性質。第3步我們假定輸入均值為0，因此E[xi]=E[wi]=0。不過這是我們的一個假設，實際情況下並不一定是這樣的，比如ReLU單元的均值就是正的。最後一步我們假定wi,xi是獨立分佈。我們想讓s的方差和輸入x的方差一致，因此我們想讓w的方差取值為1/n，又因為我們有公式Var(

相關推薦

神經網路資料預處理，正則化與損失函式

1. 引言 上一節我們講完了各種激勵函式的優缺點和選擇，以及網路的大小以及正則化對神經網路的影響。這一節我們講一講輸入資料預處理、正則化以及損失函式設定的一些事情。 2. 資料與網路的設定 前一節提到前向計算涉及到的元件(主要是神經元)設定。神經網路結構和引數設定完畢之後，我們就得到得分

CNN for Visual Recognition（6）-lecture5預處理、正則化、損失函式

本節主要講了資料預處理、正則化以及損失函式 資料預處理 關於資料預處理我們有3種常用的方式，假設資料矩陣X，假設其尺寸是[N,D]（N是資料樣本的數量，D是資料的維度）。 去均值 去均值是預處理最常見的。對待訓練的每一張圖片的特徵，都減去

神經網路優化演算法二（正則化、滑動平均模型）

1、神經網路進一步優化——過擬合與正則化 過擬合，指的是當一個模型過為複雜後，它可以很好的“記憶”每一個訓練資料中隨機噪音的部分而忘了要去“學習”訓練資料中通用的趨勢。舉一個極端的例子，如果一個模型中的引數比訓練資料的總數還多，那麼只要訓練資料不衝突，這個模型完全可以記住所有訓練資料

改善深層神經網路第一週-Regularization（正則化）

RegularizationWelcome to the second assignment of this week. Deep Learning models have so much flexibility and capacity that overfitting c

神經網路九：Regularization（正則化）與Dropout

本文主要講解神經網路中的正則化（Regularization）和Dropout，都是用了減小過擬合。正則化在機器學習領域中很重要。主要針對模型過擬合問題而提出來的。本文是觀看麥子學院的視訊整理而來。下

深度學習小白——神經網路3（資料預處理，dropout，正則化）

一、資料預處理 資料矩陣X，維度是【N*D】N是資料樣本數，D是資料維度 1.均值減法 它對資料中每個獨立特徵減去平均值，從幾何上可以理解為在每個維度上都將資料雲的中心都遷移到原點 X-=np.mean(X,axis=0) 2.歸一化 先對資料做零中心化，然後每個維度都除以

【Python資料預處理】 歸一化（按列減均值，除方差），標準化（按列縮放到指定範圍），正則化（範數）

一、標準化（Z-Score），或者去除均值和方差縮放 公式為：(X-mean)/std  計算時對每個屬性/每列分別進行。 將資料按期屬性（按列進行）減去其均值，並處以其方差。得到的結果是，對於每個屬性/每列來說所有資料都聚集在0附近，方差為1。 實現時，有兩種不同

Python資料預處理—歸一化，標準化，正則化

>>> X_train = np.array([[ 1., -1., 2.], ... [ 2., 0., 0.], ... [ 0., 1., -1.]]) ... >>> min_max_scaler = preprocessing.MinMaxScaler() >

斯坦福cs231n學習筆記（8）------神經網路訓練細節（資料預處理、權重初始化）

神經網路訓練細節系列筆記： 這一篇，我們將繼續介紹神經網路訓練細節。 一、Data Preprocessing（資料預處理） 如圖是原始資料，資料矩陣X有三種常見的資料預處理形式，其中我們假定X的大小為[N×D]（N是資料的數量，D是它們的維數

資料預處理中歸一化（Normalization）與損失函式中正則化（Regularization）解惑

背景：資料探勘/機器學習中的術語較多，而且我的知識有限。之前一直疑惑正則這個概念。所以寫了篇博文梳理下 摘要： 　　1.正則化（Regularization） 　　　　1.1 正則化的目的　 　　　　1.2 結構風險最小化（SRM）理論 　　　　1.3 L1範數

基於深度學習的CT影象肺結節自動檢測技術一——資料預處理（歸一化，資料增強，資料標記）

開發環境 Anaconda:jupyter notebook /pycharm pip install SimpleItk # 讀取CT醫學影象 pip install tqdm # 可擴充套件的Python進度條，封裝

Tensorflow 影象資料預處理，標準化

import numpy as np import random import matplotlib.pyplot as plt from PIL import Image 1.需要匯入的包 for n in range(4600): # input_d

正則化與萬用字元便於查詢和替換批量處理，使用在word，notepad++等文字編輯器中

我們常常使用查詢替換的方式來處理相關資料，可是當你要批量替換隻用一些相同字元分文字時，就會顯得很笨拙。 比如：     Line 5974: DI 10.13182/NT96-A15844     Line 6078: DI 10.1109/ISIC.1996.55623

大資料預處理，讀寫檔案為每一行資料增加一個標識ID（JAVA）

對包含多行資料的資料集進行預處理，讀入文字檔案資料集，為每一條記錄增加一個唯一的ID,並儲存成一個新的文字檔案。其中每行的ID生成規則為：每一條記錄對應生成0-33隨機數，每個數對應一個特定省份，最後原始記錄和新生成的省份標籤一起寫入新的文字檔案中。Shell終端執行語句#!

用python進行資料預處理，過濾特殊符號，英文和數字。（適用於中文分詞）

要進行中文分詞，必須要求資料格式全部都是中文，需求過濾掉特殊符號、標點、英文、數字等。當然了使用者可以根據自己的要求過濾自定義字元。 實驗環境：python、mysql 實驗目的：從資料庫讀取資料，

79、tensorflow計算一個五層神經網路的正則化損失係數、防止網路過擬合、正則化的思想就是在損失函式中加入刻畫模型複雜程度的指標

''' Created on Apr 20, 2017 @author: P0079482 ''' import tensorflow as tf #獲取一層神經網路邊上的權重，並將這個權重的L2正

資料預處理--輸入歸一化/標準化/放縮

輸入歸一化/標準化   Alex 和 Caffe中的初始化引數都是基於均值歸一化的，如果不做歸一化，會因為輸入大了一半，導致訓練失敗。這也是為什麼Caffe強制為樣本計算影象均值的原因。   這樣，畫素值[0,255]被調整成了近似[-128,128]。儘管影象資料格式規整，但是做一

資料預處理程式碼分享——機器學習與資料探勘

資料預處理分為6步： 第1步：匯入NumPy和Pandas庫。NumPy和Pandas是每次都要匯入的庫，其中Numpy包含了數學計算函式，Pnadas是一個用於匯入和管理資料集(Data Sets)的類庫。 第2步：匯入資料集。資料集一般都是.csv格式，csv

機器學習中之規範化，中心化，標準化，歸一化，正則化，正規化

一、歸一化，標準化和中心化 歸一化 （Normalization）、標準化 （Standardization）和中心化/零均值化 （Zero-centered） 標準化 資料的標準化（normalization）是將資料按比例縮放（scale），使之落入一個小的特定區間。在某些比較和評價

機器學習概念篇：監督學習、過擬合，正則化，泛化能力等概念以及防止過擬合方法總結

上個系列【數字影象處理】還將繼續更新，最近由於用到機器學習演算法，因此將之前學習到的機器學習知識進行總結，打算接下來陸續出一個【機器學習系列】，供查閱使用！本篇便從機器學習基礎概念說起！ 一、解釋監督學習，非監督學習，半監督學習的區別 監督學習、非監督學