原理講解

本次所講的內容為Batch Normalization，簡稱BN，來源於《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》，是一篇很好的paper。

1-Motivation

作者認為：網路訓練過程中引數不斷改變導致後續每一層輸入的分佈也發生變化，而學習的過程又要使每一層適應輸入的分佈，因此我們不得不降低學習率、小心地初始化。作者將分佈發生變化稱之為 internal covariate shift。

大家應該都知道，我們一般在訓練網路的時會將輸入減去均值，還有些人甚至會對輸入做白化等操作，目的是為了加快訓練。為什麼減均值、白化可以加快訓練呢，這裡做一個簡單地說明：

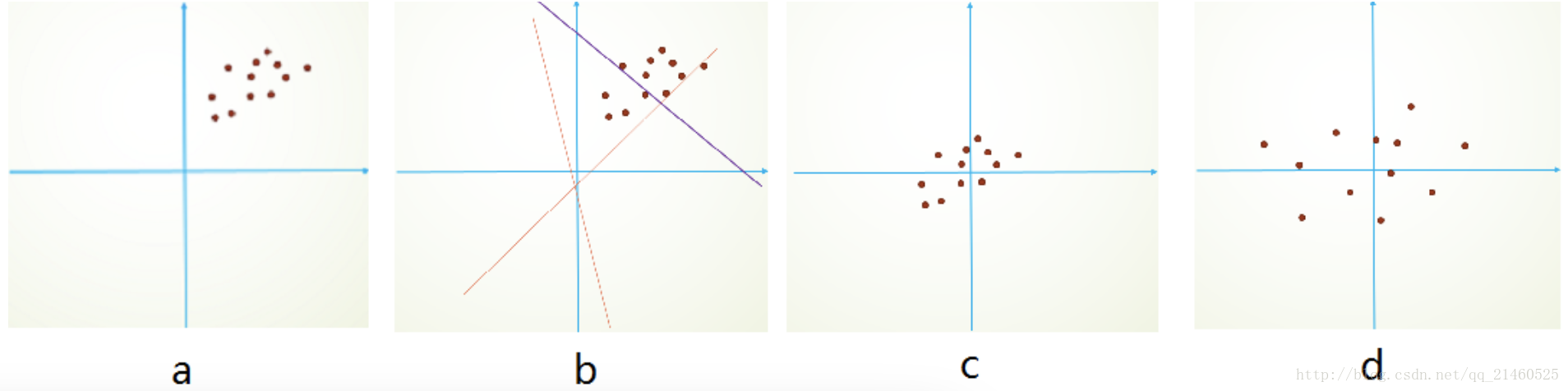
首先，影象資料是高度相關的，假設其分佈如下圖a所示(簡化為2維)。由於初始化的時候，我們的引數一般都是0均值的，因此開始的擬合y=Wx+b，基本過原點附近，如圖b紅色虛線。因此，網路需要經過多次學習才能逐步達到如紫色實線的擬合，即收斂的比較慢。如果我們對輸入資料先作減均值操作，如圖c，顯然可以加快學習。更進一步的，我們對資料再進行去相關操作，使得資料更加容易區分，這樣又會加快訓練，如圖d。

白化的方式有好幾種，常用的有PCA白化：即對資料進行PCA操作之後，在進行方差歸一化。這樣資料基本滿足0均值、單位方差、弱相關性。作者首先考慮，對每一層資料都使用白化操作，但分析認為這是不可取的。因為白化需要計算協方差矩陣、求逆等操作，計算量很大，此外，反向傳播時，白化操作不一定可導。於是，作者採用下面的Normalization方法。

2-Normalization via Mini-Batch Statistics

資料歸一化方法很簡單，就是要讓資料具有0均值和單位方差，如下式：

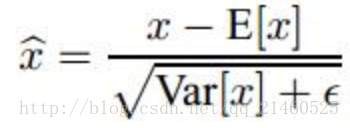
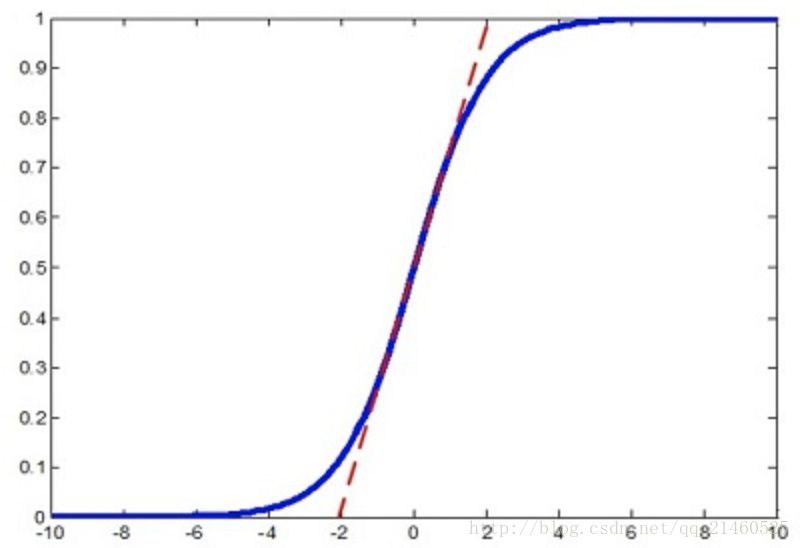
但是作者又說如果簡單的這麼幹，會降低層的表達能力。比如下圖，在使用sigmoid啟用函式的時候，如果把資料限制到0均值單位方差，那麼相當於只使用了啟用函式中近似線性的部分，這顯然會降低模型表達能力。

為此，作者又為BN增加了2個引數，用來保持模型的表達能力。
於是最後的輸出為：
這裡寫圖片描述
上述公式中用到了均值E和方差Var，需要注意的是理想情況下E和Var應該是針對整個資料集的，但顯然這是不現實的。因此，作者做了簡化，用一個Batch的均值和方差作為對整個資料集均值和方差的估計。
整個BN的演算法如下：

測試

實際測試網路的時候，我們依然會應用下面的式子：

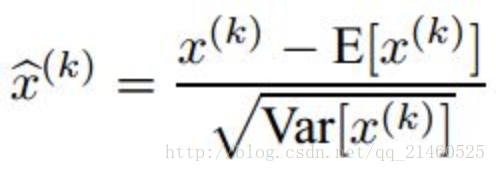
特別注意： 這裡的均值和方差已經不是針對某一個Batch了，而是針對整個資料集而言。因此，在訓練過程中除了正常的前向傳播和反向求導之外，我們還要記錄每一個Batch的均值和方差，以便訓練完成之後按照下式計算整體的均值和方差：

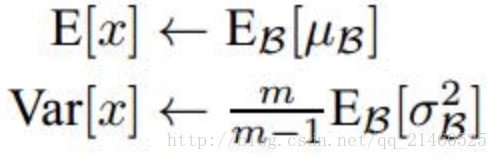
BN before or after Activation

作者在文章中說應該把BN放在啟用函式之前，這是因為Wx+b具有更加一致和非稀疏的分佈。但是也有人做實驗表明放在啟用函式後面效果更好。這是實驗連結，裡面有很多有意思的對比實驗：https://github.com/ducha-aiki/caffenet-benchmark

3-Experiments

作者在文章中也做了很多實驗對比，我這裡就簡單說明2個。
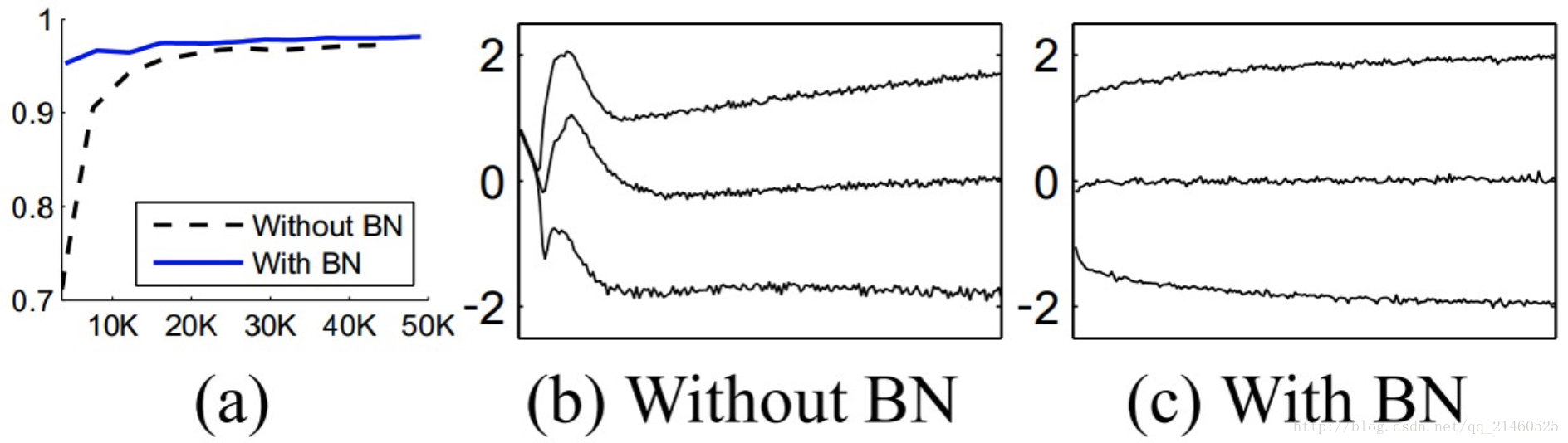
下圖a說明，BN可以加速訓練。圖b和c則分別展示了訓練過程中輸入資料分佈的變化情況。

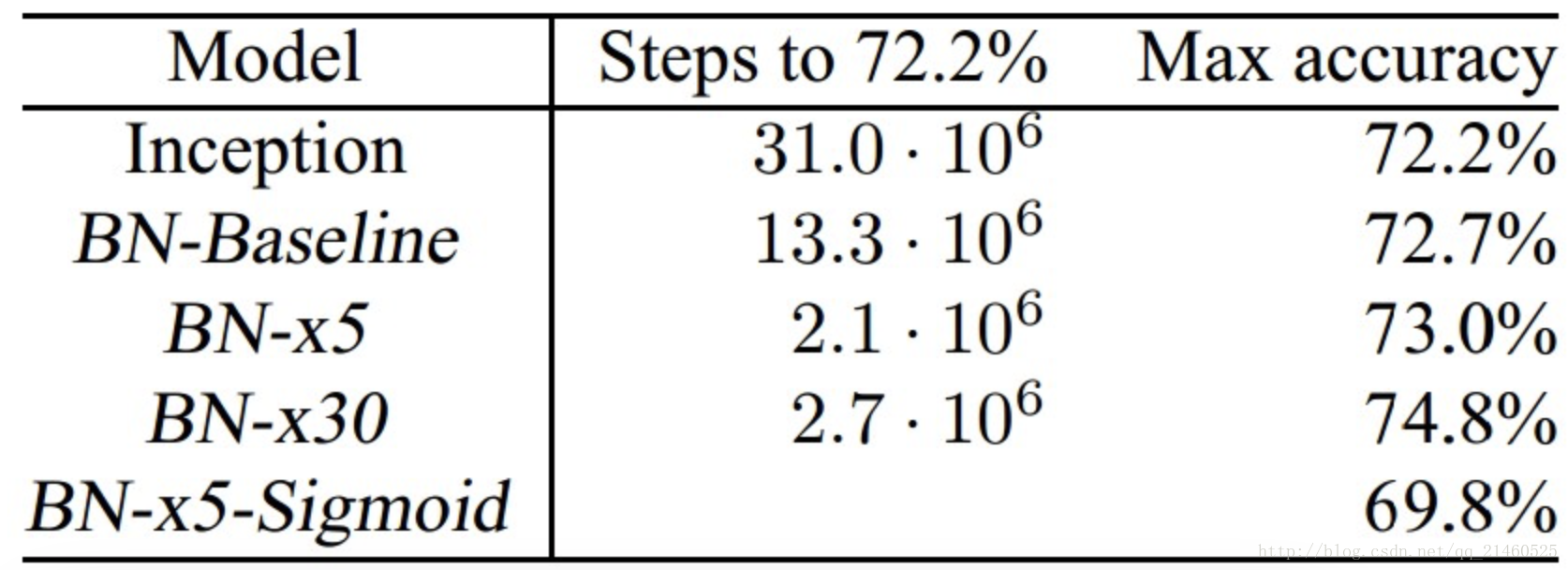
下表是一個實驗結果的對比，需要注意的是在使用BN的過程中，作者發現Sigmoid啟用函式比Relu效果要好。

程式碼實現：

BatchNormalization是神經網路中常用的引數初始化的方法。其演算法流程圖如下：
這裡寫圖片描述

我們可以把這個流程圖以閘電路的形式展開，方便進行前向傳播和後向傳播：
這裡寫圖片描述

那麼前向傳播非常簡單，直接給出程式碼：

def batchnorm_forward(x, gamma, beta, eps):

  N, D = x.shape
  #為了後向傳播求導方便，這裡都是分步進行的
  #step1: 計算均值
  mu = 1./N * np.sum(x, axis = 0)

  #step2: 減均值
  xmu = x - mu

  #step3: 計算方差
  sq = xmu ** 2
  var = 1./N * np.sum(sq, axis = 0)

  #step4: 計算x^的分母項
  sqrtvar = np.sqrt(var + eps)
  ivar = 1./sqrtvar

  #step5: normalization->x^
  xhat = xmu * ivar

  #step6: scale and shift
  gammax = gamma * xhat
  out = gammax + beta

  #儲存中間變數
  cache =  (xhat,gamma,xmu,ivar,sqrtvar,var,eps)

  return out, cache

反向傳播則是求導的過程，這裡特別要小心，由於閘電路中有多個支路，求導時要進行加和。

def batchnorm_backward(dout, cache):

  #解壓中間變數
  xhat,gamma,xmu,ivar,sqrtvar,var,eps = cache

  N,D = dout.shape

  #step6
  dbeta = np.sum(dout, axis=0)
  dgammax = dout
  dgamma = np.sum(dgammax*xhat, axis=0)
  dxhat = dgammax * gamma

  #step5
  divar = np.sum(dxhat*xmu, axis=0)
  dxmu1 = dxhat * ivar #注意這是xmu的一個支路

  #step4
  dsqrtvar = -1. /(sqrtvar**2) * divar
  dvar = 0.5 * 1. /np.sqrt(var+eps) * dsqrtvar

  #step3
  dsq = 1. /N * np.ones((N,D)) * dvar
  dxmu2 = 2 * xmu * dsq #注意這是xmu的第二個支路

  #step2
  dx1 = (dxmu1 + dxmu2) 注意這是x的一個支路


  #step1
  dmu = -1 * np.sum(dxmu1+dxmu2, axis=0)
  dx2 = 1. /N * np.ones((N,D)) * dmu 注意這是x的第二個支路

  #step0 done!
  dx = dx1 + dx2

  return dx, dgamma, dbeta

要注意的就是求導時遇到多個支路的情況要進行累加。表示式複雜的話還是分步進行比較不容易出錯。