【轉載】浮點數運算的定點數程式設計
我們使用的處理器一般情況下,要麼直接支援硬體的浮點運算,比如某些帶有FPU的器件,要麼就只支援定點運算,此時對浮點數的處理需要通過編譯器來完成。在支援硬體浮點處理的器件上,對浮點運算的程式設計最快捷的方法就是直接使用浮點型別,比如單精度的float來完成。但是在很多情況下,限於成本、物料等因素,可供我們使用的只有一個定點處理器時,直接使用float型別進行浮點型別的運算會使得編譯器產生大量的程式碼來完成一段看起來十分簡單的浮點數學運算,造成的後果是程式的執行時間顯著加長,且其佔用的資源量也會成倍地增加,這就涉及到了如何在定點處理器上對浮點運算進行高效處理的問題。
本文引用地址:http://www.eepw.com.cn/article/263475.htm既然是定點處理器,那麼其對定點數,或者說字面意義上的“整數”進行處理的效率就會比它處理浮點型別的運算要高的多。所以在定點處理器上,我們使用定點的整數來代表一個浮點數,並規定整數位數和小數位數,從而方便地對定點數和浮點數進行轉換。以一個32位的定點數為例,假設轉換因子為Q,即32位中小數的位數為Q,整數位數則為31-Q(有符號數的情況),則定點數與浮點數的換算關係為:
定點數=浮點數×2^Q
例如,浮點數-2.0轉換到Q為30的定點數時,結果為:
定點數=-2×2^30=-2147483648
32位有符號數的表示範圍是:-2147483648到2147483647。如果我們把有符號定點數的最大值2147483647轉換為Q為30對應的浮點數,則結果為:
浮點數2147483647/2^30=1.999999999
從上面的兩個計算例子中也可以看出,在Q30格式的情況下,最大的浮點數只能表示到1.999999999,如果我們想把浮點數2.0轉換為Q30的定點數,則產生了溢位,即造成了1e-9的截斷誤差。在此我們列出Q0到Q30對應的範圍和解析度如下表所示: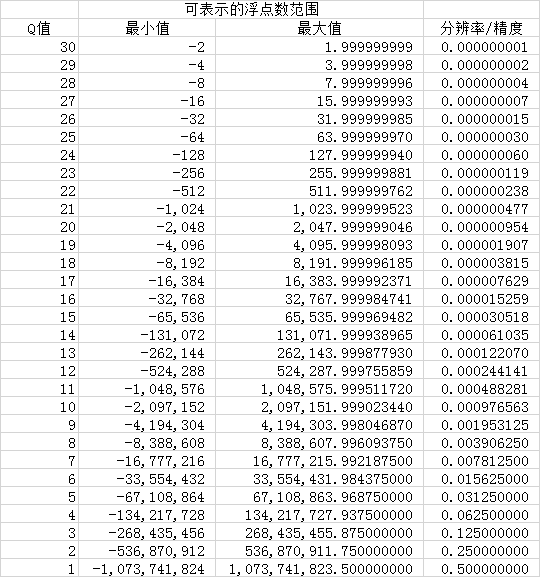
如果你嫌自己計算麻煩的話,可以藉助Matlab的命令來求取它們的轉換,例如,在Matlab的命令視窗中輸入:
q = quantizer('fixed', 'ceil', 'saturate', [32 30]);
FixedNum=bin2dec(num2bin(q,1.999999999));
回車之後就可以看到1.999999999轉成Q30之後的定點數了。
弄清楚了單個浮點數和定點數之間的轉換關係,接下來就需要了解一下兩個定點數所代表的浮點數進行運算時,是如何轉換的了。根據乘法的結合律、分配率,浮點數轉換之後的定點數是可以直接運算的,例如:
1. 不同Q格式的轉換
設有定點數Fixed1=Float1*2^Q1,如果把它用為Q2這個不同精度/表示範圍的定點數來表示,則有Fixed2=Float1*2^Q2。所以不同的Q格式直接的轉換為:
Fixed2=Fixed1*2^Q2/2^Q1=Fixed1*2^(Q2-Q1)
因為Fixed1、Fixed2都是定點數,所以在C程式設計的情況下,我們可以使用高效的左移、右移操作來完成這個乘以2^(Q2-Q1)的操作。
2. 兩個相同Q格式的定點數:
Fixed1=Float1*2^Q
Fixed2=Float2*2^Q
則加法操作為:
Float1+Float2=Fixed1/2^Q+Fixed/2^Q=(Fixed1+Fixed2)/2^Q
對於上述的加法操作,如果定點數的和Fixed1+Fixed2超過了32位整數的極值,則會發生溢位現象,造成結果的不正確,此時我們只能先損失一倍的精度,把Float1、Float2的Q值變為Q-1.
乘法操作為:
Float1*Float2=Fixed1/2^Q*Fixed/2^Q= Fixed1*Fixed2/2^(2Q)
同樣的道理,如果Fixed1*Fixed2之後的定點數超過了32位整數的極值,則我們也需要提前對它們進行一下折算,變換一下它們的Q值。這就涉及到對結果的一個預估問題,也是定點程式設計不如浮點程式設計簡單、高效的不足之一。
3. 兩個不同Q格式的定點數:
Fixed1=Float1*2^Q1
Fixed2=Float2*2^Q2
運算的規則是結合了前面的兩種情況,只不過多了額外的轉換工作:要麼把其中的一個Q1格式的定點數先轉換為另一個Q2格式,要麼把它們都轉換為一箇中間值Q3格式的定點數,然後再進行運算。
