題意：

給定n*m的格子，每個格子被染成了黑色或者白色。現在要用1 * 2 的磚塊覆蓋這些格子，要求塊與塊之間互相不重疊，且覆蓋了所有白色的格子，但不覆蓋任意一個黑色格子。求一個有多少種覆蓋方法，輸出方案數對M取餘後的結果。

輸入:

n= 3

m= 4

每個格子的顏色如下所示（.表示白色，x表示黑色）

…

.x.

…

輸出：

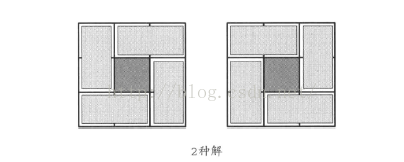
2

分析:

由於黑色的格子不能被覆蓋，因此used裡對應的位置總是false。對於白色的格子，如果現在要在(i,j)位置上放置磚塊，那麼由於總是從最上方的可放的格子開始放置，因此對應(i’,j’)<(i.j)（按字典序比較）的(i’,j’)總有 used[i’][j’]=true成立。

此外，由於磚塊的大小為1*2，因此對於每一列j’在滿足(i’,j’)>=(i.j)的所有i’中，除了最小的i’之外都滿足used[i’][j’]=false。因此，不確定的只有每一列裡還沒有查詢的格子中最上面的一個，共m個。從而可以把這m個格子通過狀態壓縮編碼進行記憶化搜尋。按照之前的狀態壓縮DP的寫法就得到了下面的程式。

int dp[1 << maxn];      //DP陣列（滾動陣列迴圈利用）

void solve()
{
    int *crt = dp[0], *next = dp[1];
    crt[0] = 1;
    for (int i = n - 1; i >= 0; i--){
        for (int j = m - 1; j >= 0; j--){
            for (int used = 0; used < 1 << m; used++){
                if ((used >> j & 1) || color[i][j]){
                    //不需要在(i, j)放置磚塊
                    next[used] = crt[used & ~(1 << j)];
                }
                else{
                    //嘗試2种放法
                    int res = 0;
                    //橫著放
                    if (j + 1 < m && !(used >> (j + 1) & 1) && !color[i][j + 1]){
                        res += crt[used | 1 <<< (j + 1)];
                    }
                    //豎著放
                    if (i + 1 < n && !color[i + 1][j]){
                        res += crt[used | 1 << j];
                    }
                    next[used] = res % M;
                }
            }
            swap(crt, next);
        }
    }
    printf("%d\n", crt[0]);
}