15-1.有向無環圖中的最長加權簡單路徑

動態規劃的思想就是從窮舉法中簡化的過程，求解S結點->E結點的最長簡單路徑，權重用w（E）表示，w（E）= max{w(B)+2,w(D)+1}，繼續劃分子問題，w（B）=w（A）+6，w（D）=max{w（B）+1，w（C）+3}，等等。採用自底向上方法，求出w（S），w（A），w（c）直到w（E），並將其值存在一個數組中，這樣每次求解問題是可以在陣列中找到子問題的最優解。最後就可以得到S結點到E結點最長路徑的權重。

然而，如何求解最長路徑呢？我們可以在max函式比較的過程中，記錄下來較大的那個結點，即是最長路徑所需經過的結點，最後組成的結點陣列即是最長簡單路徑。

15-2.最長迴文子序列（非最長迴文子串）

子串是連續的，子序列是非連續的，子串總的個數為n(n+1)/2+1個，子序列為2^n個。顯然用窮舉法是不現實的。

我們觀察一下是否符合最優子結構:

假設一個長度為n字串S的最長迴文子序列的長度為c，如果S[1]==S[n]，那麼必然存在S[2，n-1]的最長迴文子序列的長度為c-2；如果S[1]!=S[n]，那麼S[1,n-1]和S[2，n]，兩者較長的最長迴文子序列的長度為c，表示式為：

i>j時，c[i,j]=0;

i=j時，c[i,j]=1;

i<j且S[i]=S[j]時，c[i,j]=c[i-1,j-1]+2;

i<j且S[i]!=S[j]時，c[i,j]=max{c[i,j-1]，c[i+1,j]};

當我們求解c[i,j]時，它的子問題必然是最優的，符合最優子結構，而且在求解時重複用到了子問題的解，符合子問題重疊，則使用動態規劃求解問題。
我們採用自底向上方法，以子串長度len為一層迴圈，i為一層迴圈，O(n^2)時間內即可求出結果。到此，我們可以求解出最長迴文子序列的長度c[1,n]，如何求解出子序列呢？

我們可以在判斷S[i]和S[j]相等時，去記錄迴文字元，裝在一個數組r中。最終迴圈結束時，判斷c[1,n]的值若為2len(r)，則說明迴文字串長度為偶數，若為2len(r)+1，長度為奇數，中間值為S[len(r)+1]（中間值並不是確定的，可以取任一個在迴文序列中間的字元）。

15-3.雙調歐幾里得旅行商問題

1. 先找出最優子結構，先把n個結點按x座標從小到大排序，最短路程我們用dp(n,n)來表示。dp(n-1,n)則表示從點n-1出發，到達最左，又回到點n的最短路程，那麼
   dp(n,n)=dp(n-1,n)+d(n-1,n)  //結點n必然與結點n-1相連，d(n-1,n)代表兩的直線距離。
   要求dp(n,n)的最優解，dp(n-1,n)必然也是最優解。dp(n-1,n)如何求最優解呢？假設與結點n直接相連的結點為k(1=<k<n-1)，則路程為dp(n-1,k)+d(k,n)，遍歷所有的k值，取出最小值即為dp(n-1,n)的最優解，表示式為
   dp(n-1,n)=min{dp(n-1,k)+d(k,n)}(1=<k<n-1)
   下面要求dp(n-1,k)(1=<k<n-1)的最優解了。
2. 子問題遞迴式，用dp(i,j)來表示從結點i到結點j的路程(i<=j)，這裡要注意，dp(i,j)代表從結點i出發，到達最左邊結點，然後回到結點j的路程，j右側的所有結點當做不存在，可將子問題分為三種情況:
   i=j時，dp(i,i)=dp(i-1,i)+d(i-1,i)
   i=j-1時，dp(i,i+1) = min{dp(i,k)+d(k,i+1)}(1=<k<i)
   i<j-1時，dp(i,j) = dp(i,j-1)+d(j-1,j)
3. 採用自底向上方法，最小子問題為dp(1,1)=0,dp(1,2)=d(1,2)

   for j = 3 to n
       for i = 1 to j - 2 //i<j-1的情況
           dp(i,j) = dp(i,j-1)+d(j-1,j)
       dp(j-1,j)=int_max
       for k = 1 to j - 2 //i=j-1的情況
           dis = dp(j-1,k)+d(k,j)
           if(dis<dp(j-1,j))
               dp(j-1,j) = dis
   dp(n,n) = dp(n-1,n)+d(n-1,n) //結果

15-4.整齊列印

定義lc[i,j]為第i到第j個單詞裝入一行時的額外空格數的立方,如下表示，extras[i,j]是額外空格數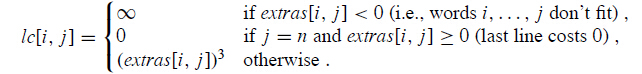

c[j]表示從1到j個單詞的最小額外空格數立方和

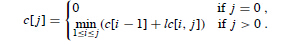
15-8.基於接縫裁剪的影象壓縮

c[i,j]記錄接縫走到當前畫素的最低破壞度，r[i,j]記錄當前結點來自於上一行的那個畫素（用-1,0,1分別表示左上，正上和右上方向）。
從第一行開始，c[i,j]只有當前畫素的破壞度，直接賦值即可； 第i行，每個畫素的上一個畫素來源一共有三個，左上、正上和右上方，每次計算c[i,j]時，需要去三種情況中破壞度最低的情況然後加上當前畫素的破壞度，就是接縫走到當前畫素的最低破壞度。同時更新r[i,j]. 第n行，接縫走到這裡結束，在第n行找出最小值，c[i,j]即為最低的破壞度，通過r[i,j]向上走，直到第一行，所經的路徑即為破壞度最小的接縫。