Captain Dialog 2009-09-18

    三維建模和等值面的繪製過程中，需要經常使用三角形網格對資料體進行構面。而三角形的生成基於Delaunay三角剖分的演算法實現的。前段時間一直在考慮資料體的任意剖面切割該怎麼做，但是一直被兩個問題所困擾，一個就是交點問題，然後就是對所求交點進行繪製問題（三角形網格面構造）。終於在半個月後有了一點收穫。

1 Delaunay三角剖分原理

     三角剖分演算法可以分為針對二維的區域性剖分和三維的全域性剖分演算法。在二維情況下建立的基於簡單的三角形構面的方式，而三維情況下則是需要建立基於四面體的方式構造空間曲面。在遇到三維空間散亂點的構面問題時，可以直接採用三維Delaunay剖分，亦可先將三維座標預處理轉換到二維座標系中，間接的採用二維Delaunay剖分演算法。想著用最簡單的方式實現功能的時候，就選擇了第二種方式。

    關於二維的Delaunay三角剖分原理，文獻資料相當多，隨便一搜就是一大堆，網上也有很不錯的介紹：

關於生成三角形網格的演算法也是很多，我選擇了稍微老套點的生長法，實現起來還算是思路清晰。

2 三維空間散亂點Delaunay三角剖分程式實現

     這個過程中，我們首先需要實現的就是三維座標向二維座標的轉換。引數化的方程組求解可以參考：

http://z.baidu.com/question/81807904.html?fr=qrl&cid=1071&index=4&fr2=query 其中需要我們注意的就是自己需要投影的平面方程了。比如需要製作剖切面，找到它的法向以後，中間還需要再加上一個步驟，那就是實現空間三維點投影到另外的一個空間平面上的過程，然後再接著進行向二維座標的轉換。任意方向剖切面的演算法實現步驟： Step1

求取空間任意方向剖切面的方程。（利用三點確定平面原理+點法式平面方程）； Step2 求取剖切面與三維資料體的交點； Step3 根據得到的交點資料集進行座標投影，將三維座標點投影到剖切面上； Step4 再將完成投影后的三維資料點集進行二維直角座標系的引數化求解（投影到（U，V）二維座標系中）；             可以首先確定一個向量U，選為第一個點到距離第一個點最遠的另一點的向量；             然後確定另一個向量V，選為垂直於U和剖切面發向量的方向向量； Step5 進行鍼對處理後的二維資料點集的Delaunay三角剖分； Step6 將資料還原為三維座標。 程式實現程式碼（VC++）：

3 三維空間任意剖面實現

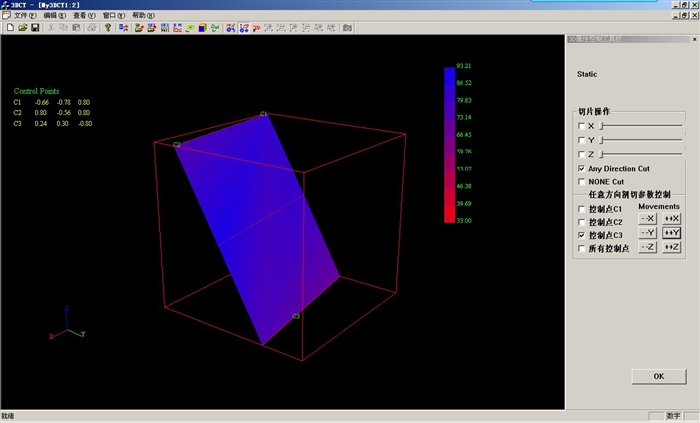
本文引用地址：http://blog.sciencenet.cn/blog-244606-256392.html