2. 程式人生 > >經典排序演算法分析及實現

經典排序演算法分析及實現

阿新 • • 發佈：2019-02-15

一、排序概念

1. 排序：將一組雜亂無章的資料按照一定的規律組織起來，就稱為排序。
2. 資料表：待排序的資料元素的有限集合。
3. 排序碼：通常資料元素有多個屬性域，其中有一個屬性域可以用來區分元素，作為排序依據，該域即為排序碼。


* 若在資料表中各個元素的排序碼各不相同，這種排序碼稱為主排序碼。
* 按照主排序碼進行排序，排序的結果是唯一的。
* 按照次排序碼進行排序，排序結果不唯一。

二、排序演算法的穩定性
如果在元素序列中有兩個元素R[i]和R[j]，他們的排序碼K[i]==K[j]，且在排序之前，R[i]在R[j]前面。若在排序後，R[i]仍然在R[j]前面，則稱這個演算法是穩定的。否則，這個演算法是不穩定的。

三、經典排序演算法
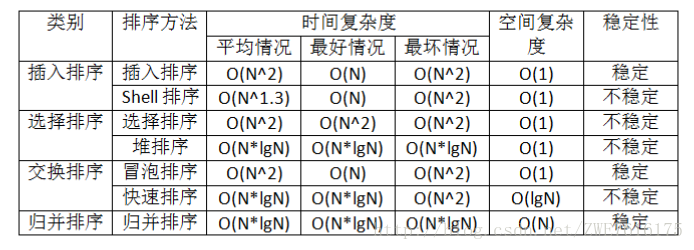
這裡寫圖片描述

演算法總結
這裡寫圖片描述

3.1.插入排序

3.1.1直接插入排序
基本思想：
當插入第i個元素時，前面的array[0]、array[1]、array[2]……array[i-1]已經排好序，此時用array[i]的排序碼與array[i-1]、array[i-2]……的排序碼進行比較，找到插入位置將array[i]插入，原來位置上的元素順序右移。

動畫演示：
這裡寫圖片描述

程式碼實現：

////////////////////插入排序//////////////////////////
//插入排序
//時間複雜度：O(n^2)
//空間複雜度：O(1)
//穩定性：穩定
void InsertSort(int* array,int size)
{
    //[0,end] end+1插入
 

    for (int i = 1; i < size; ++i)
    {
        int key = array[i];//當前元素的排序碼
        int end = i - 1;
        while (end >= 0 && array[end] > key)//找插入位置
        {
            array[end + 1] = array[end];
            end--;
        }
        array[end + 1] = key;//插入
    }
}

改進：二分法插入排序
優點：查詢更快，減少比較操作的次數，效率更高。

//二分插入排序
void InsertSort_OP(int* array, size_t size)
{
    for (int i = 1; i < size; i++)
    {
        //在已序序列中查詢待插入元素的位置
        int left = 0;
        int right = i - 1;
        int key = array[i];

        while (left <= right)
        {
            int mid = left + ((right - left) >> 1);
            if (key < array[mid])
                right = mid - 1;
            else
                left = mid + 1;
        }

        //搬移元素
        int end = i - 1;
        while (end >= left)
        {
            array[end + 1] = array[end];
            end--;
        }

        //插入元素
        array[left] = key;
    }
}

3.1.2 希爾排序
基本思想：
希爾排序(Shell’s Sort)是插入排序的一種又稱“縮小增量排序”（Diminishing Increment Sort），是直接插入排序演算法的一種更高效的改進版本。希爾排序是非穩定排序演算法。該方法因D.L.Shell於1959年提出而得名。
希爾排序是把記錄按下標的一定增量分組，對每組使用直接插入排序演算法排序；隨著增量逐漸減少，每組包含的關鍵詞越來越多，當增量減至1時，整個檔案恰被分成一組，演算法便終止。

動畫實現：
這裡寫圖片描述

程式碼實現：

//希爾排序
//時間複雜度：O(n^1.25 ~ 1.6n^1.25)
//空間複雜度：O(1)
//穩定性：穩定
//適用場景：資料量大
/*
void ShellSort(int* array, size_t size)
{
    int gap = 3;
    while (gap)
    {
        for (size_t i = gap; i < size; ++i)
        {
            int key = array[i];
            int end = i - gap;

            //找到當前需要插入元素的位置
            while (end >= 0 && array[end] > key)
            {
                array[end + gap] = array[end];
                end -= gap;
            }

            //插入元素
            array[end + gap] = key;
        }
        gap--;
    }
}
*/

void ShellSort(int* array, size_t size)
{
    int gap = size;
    while (gap > 1)
    {
        gap = gap / 3 + 1;//經過大量計算得到此類方法時間複雜度較低
        for (size_t i = gap; i < size; ++i)
        {
            int key = array[i];
            int end = i - gap;

            //找到當前需要插入元素的位置
            while (end >= 0 && array[end] > key)
            {
                array[end + gap] = array[end];
                end -= gap;
            }

            //插入元素
            array[end + gap] = key;
        }
    }
}

3.2 選擇排序

3.2.1 選擇排序

基本思想：
選擇排序（Selection sort）是一種簡單直觀的排序演算法。它的工作原理是每一次從待排序的資料元素中選出最小（或最大）的一個元素，存放在序列的起始位置，直到全部待排序的資料元素排完。 選擇排序是不穩定的排序方法（比如序列[5， 5， 3]第一次就將第一個[5]與[3]交換，導致第一個5挪動到第二個5後面）。

動畫實現：
這裡寫圖片描述

程式碼實現：

//選擇排序
//時間複雜度：O(N^2)
//空間複雜度：O(1)
//穩定性：不穩定
void SelectSort(int* array, size_t size)
{
    int begin = 0;
    int end = size - 1;

    while (begin < end)
    {
        int min = begin;
        int max = end;

        for (size_t i = begin; i < end; ++i)
        {
            if (array[i] < array[min])
                min = i;
            if (array[i] > array[max])
                max = i;
        }

        swap(array[begin], array[min]);
        //修正
        if (min == end)
            min = max;

        swap(array[end], array[max]);
        ++begin;
        --end;
    }
}

3.2.2 堆排序
基本思想：
將待排序序列構造成一個大頂堆，此時，整個序列的最大值就是堆頂的根節點。將其與末尾元素進行交換，此時末尾就為最大值。然後將剩餘n-1個元素重新構造成一個堆，這樣會得到n個元素的次小值。如此反覆執行，便能得到一個有序序列了

動畫實現：
這裡寫圖片描述

程式碼實現：

//堆排序之向下調整
void AdjustDown(int* array, size_t size, int root)
{
    int parent = root;
    int child = parent * 2 + 1;
    while (child < size)
    {
        if (child + 1 < size && array[child + 1] > array[child])
        {
            child++;
        }

        if (array[child] > array[parent])
        {
            swap(array[child], array[parent]);
            parent = child;
            child = child * 2 + 1;
        }
        else
        {
            break;
        }
    }
}

//堆排序
//時間複雜度：O(n*lgN)
//空間複雜度：O(1)
//穩定性：不穩定
void HeapSort(int* array, size_t size)
{
    //調整堆
    for (int i = (size - 2) / 2; i >= 0; --i)
    {
        AdjustDown(array, size, i);//向下調整
    }

    //排序
    int end = size - 1;
    while (end >= 0)
    {
        swap(array[end], array[0]);
        AdjustDown(array, end, 0);
        end--;
    }
}

3.3 交換排序

3.3.1 氣泡排序
基本思想：
設序列中有n個數據元素，迴圈進行n-1趟如下排序：
第1趟：依次比較相鄰兩個資料元素(i = 0,1,2,…, n-2),若array[i]>array[i+1],則交換兩個元
素，否則不交換，這樣數值最大的資料元素將被防止在a[n-1]中；
第2趟：資料個數減1，即資料元素個數為n-1，操作方式和1類似，排完之後資料序列中的次大元素
儲存在array[n-2]中；
當n-1趟結束時，排序結束。

動畫實現：
這裡寫圖片描述

程式碼實現：

//氣泡排序
//時間複雜度：O(N^2)
//空間複雜度：O(1)
//穩定性：穩定
void BubbleSort(int* array, size_t size)
{
    for (size_t end = size; end > 0; --end)
    {
        bool exchange = false;
        for (size_t i = 1; i < end; i++)
        {
            if (array[i - 1]>array[i])
            {
                swap(array[i - 1], array[i]);
                exchange = true;
            }
        }

        if (exchange == false)
            break;
    }
}

氣泡排序與插入排序的區別：插入排序更優
1 2 3 5 4
氣泡排序：(n-1)+(n-2)
插入排序：n

3.3.2 快速排序

基本思想：
通過一趟排序將待排記錄分隔成獨立的兩部分，其中一部分記錄的關鍵字均比另一部分的關鍵字小，則可分別對這兩部分記錄繼續進行排序，以達到整個序列有序。

遞迴實現：

//遞迴實現
void QuickSort(int* array, int left, int right)
{
    if (left >= right)
        return;

    /*
    //小區間優化
    if (right - left + 1 < 5)//16
    {
        InsertSort(array + left, right - left + 1);
        return;
    }
    */

    int div = PartSort1/PartSort2/PartSort3/PartSort4(array, left, right);//快排分開的位置

    QuickSort(array, left, div - 1);//[left,div-1]
    QuickSort(array, div + 1, right);//[div+1,right]
}

非遞迴實現：

#include <stack>
//非遞迴
void QuickSortNor(int* array, int left, int right)
{
    stack<int> s;
    s.push(right);
    s.push(left);

    while (!s.empty())
    {
        int begin = s.top();
        s.pop();
        int end = s.top();
        s.pop();

        int div = PartSort1/PartSort2/PartSort3/PartSort4(array, begin, end);
        if (begin < div - 1)
        {
            s.push(div - 1);
            s.push(begin);
        }
        if (div + 1 < end)
        {
            s.push(end);
            s.push(div + 1);
        }
    }
}

快排分開位置的幾種方法：
1.begin找大,end找小

int PartSort1(int* array, int begin, int end)
{
    int& key = array[end];//將最後一個元素作為中間元素
    while (begin < end)
    {
        while (begin < end && array[begin] <= key)//注意：等號的情況得考慮進去，防止第一個元素與最後一個元素相等
            ++begin;
        while (begin < end && array[end] >= key)
            --end;

        swap(array[begin], array[end]);
    }

    swap(array[begin], key);
    return begin;
}
//優化
//三數取中---獲取中間元素的下標
int GetMidIndex(int* array, int begin, int end)
{
    int mid = begin + ((end - begin) >> 1);

    //begin mid
    if (array[mid] > array[begin])
    {
        if (array[end] > array[mid])//begin mid end
            return mid;
        else if (array[end] > array[begin])//begin end mid
            return end;
        else
            return begin;
    }

    //mid begin
    else
    {
        if (array[end] < array[mid])//end mid begin
            return mid;
        else if (array[end] >array[begin])//mid begin end
            return begin;
        else
            return end;
    }
}

2.左右指標法

int PartSort2(int* array, int begin, int end)
{
    int mid = GetMidIndex(array, begin, end);
    swap(array[mid], array[end]);

    int& key = array[end];//將最後一個元素作為中間元素
    while (begin < end)
    {
        while (begin < end && array[begin] <= key)//注意：等號的情況得考慮進去，防止第一個元素與最後一個元素相等
            ++begin;
        while (begin < end && array[end] >= key)
            --end;

        swap(array[begin], array[end]);
    }

    swap(array[begin], key);
    return begin;
}

3.挖坑法

int PartSort3(int* array, int begin, int end)
{
    int& key = array[end];

    while (begin < end)
    {
        while (array[begin] < key)
        {
            ++begin;
        }
        array[end] = array[begin];//填坑

        while (array[end] > key)
        {
            --end;
        }
        array[begin] = array[end];//填坑
    }
    array[begin] = key;
    return begin;
}

4.前後指標法

int PartSort4(int* array, int begin, int end)
{
    int prev = begin - 1;
    int cur = begin;
    int key = array[end];

    while (cur < end)
    {
        if (array[cur] < key&&++prev != cur)//cur找小
            swap(array[cur], array[prev]);//交換，小的放左，大的放右

        ++cur;
    }

    swap(array[++prev], array[end]);
    return prev;
}

3.4 歸併排序
基本思想：
基本思想：將待排序的元素序列分成兩個長度相等的子序列，為每一個子序列排序，然後將他們合併成一個序列。合併兩個子序列的過程稱為兩路歸併。

動畫實現：
這裡寫圖片描述

程式碼實現：

//時間複雜度：O(N*logN)
//空間複雜度：O(N)
//穩定性：穩定
#include <assert.h>
//[left,right]
void _MergeSort(int* array, int left, int right, int* tmp)
{
    if (left >= right)
        return;

    int mid = left + ((right - left) >> 1);
    //[left,mid] [mid+1,right] 均為有序區間
    _MergeSort(array, left, mid, tmp);
    _MergeSort(array, mid + 1, right, tmp);

    int begin1 = left;
    int end1 = mid;
    int begin2 = mid + 1;
    int end2 = right;
    int index = left;

    //從頭開始比較大小，小的放在新空間中，繼續往後走
    while (begin1 <= end1 && begin2 <= end2)
    {
        if (array[begin1] < array[begin2])
            tmp[index++] = array[begin1++];
        else
            tmp[index++] = array[begin2++];
    }

    //[begin2,end2]走完,將[begin1,end1]剩下的元素放入新空間中
    while (begin1 <= end1)
    {
        tmp[index++] = array[begin1++];
    }

    while (begin2 <= end2)
    {
        tmp[index++] = array[begin2++];
    }
    memcpy(array + left, tmp + left, (right - left + 1)*sizeof(int));
}

void MergeSort(int* array, size_t size)
{
    assert(array);
    //開闢一個新空間
    int* tmp = new int[size];
    _MergeSort(array, 0, size - 1, tmp);
    delete[] tmp;
}

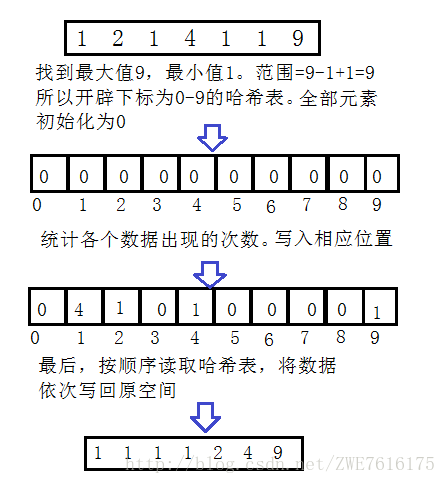
3.5 計數排序
基本思想：
利用雜湊的方法，將每個資料出現的次數都統計下來。雜湊表是順序的，所以我們統計完後直接遍歷雜湊表，將資料再重寫回原資料空間就可以完成排序。

動畫實現：
這裡寫圖片描述

程式碼實現：

//時間複雜度：O(N+資料範圍)
//空間複雜度：O(最大數-最小數)
//場景：正整數排序
void CountSort(int* array, size_t size)
{
    //計算相對位置
    int min = array[0];
    int max = array[0];

    for (size_t i = 0; i < size; ++i)
    {
        if (array[i] < min)
            min = array[i];
        if (array[i] > max)
            max = array[i];
    }

    int range = max - min + 1;
    int* counts = new int[range];
    memset(counts, 0, range*sizeof(int));

    for (size_t i = 0; i < size; ++i)
    {
        counts[array[i] - min]++;//相對位置
    }

    //藉助counts陣列將元素放入原空間中
    int j = 0;
    for (size_t i = 0; i < range; ++i)
    {
        while (counts[i]--)
        {
            array[j++] = i + min;
        }
    }

    //釋放輔助空間
    delete[] counts;
}

3.6 基數排序
基本思想：
基數排序是按照低位先排序，然後收集；再按照高位排序，然後再收集；依次類推，直到最高位。有時候有些屬性是有優先順序順序的，先按低優先順序排序，再按高優先順序排序。最後的次序就是高優先順序高的在前，高優先順序相同的低優先順序高的在前。基數排序基於分別排序，分別收集，所以是穩定的。

①LSD–Least Significant Digit first 從低位（個位）向高位排。
②MSD– Most Significant Digit first 從高位向低位（個位）排。

動畫實現：
這裡寫圖片描述

程式碼實現：

//LSD(先排低位) MSD(先排高位)
//時間複雜度：O(N*基數)
//空間複雜度：O(N)
//場景：正整數排序
void LSDSort(int* array, size_t size)
{
    //統計資料中最大數的位數
    int digits = 1;//至少是個位數
    int base = 10;
    for (size_t i = 0; i < size; ++i)
    {
        while (array[i] >= base)
        {
            ++digits;
            base *= 10;
        }
    }

    int* buckets = new int[size];//開闢臨時空間
    base = 1;
    for (size_t i = 0; i < digits; ++i)
    {
        //0~9號桶中存放資料的個數
        int counts[10] = { 0 };
        for (size_t i = 0; i < size; ++i)
        {
            int num = (array[i]/base) % 10;
            counts[num]++;
        }

        //0~9號桶第一個資料的起始位置
        int starts[10] = { 0 };
        for (size_t i = 1; i < 10; ++i)
        {
            starts[i] = starts[i - 1] + counts[i - 1];
        }

        for (size_t i = 0; i < size; ++i)
        {
            int num = (array[i] / base) % 10;//個位是幾，num表示幾號桶
            int index = starts[num]++;//每放入一個數據在桶裡，就給起始位置++
            buckets[index] = array[i];//將資料放入桶中
        }

        memcpy(array, buckets, sizeof(int)*size);
        base *= 10;
    }

    delete[] buckets;
}

測試程式碼：

void test()
{
    int array[] = { 3, 4, 1, 5, 8, 6, 9, 0 };
    //InsertSort(array, sizeof(array) / sizeof(array[0]));
    //InsertSort_OP(array, sizeof(array) / sizeof(array[0]));
    //ShellSort(array, sizeof(array) / sizeof(array[0]));
    //SelectSort(array, sizeof(array) / sizeof(array[0]));
    //HeapSort(array, sizeof(array) / sizeof(array[0]));
    //BubbleSort(array, sizeof(array) / sizeof(array[0]));
    //QuickSort(array, 0, sizeof(array) / sizeof(array[0]) - 1);
    //QuickSortNor(array, 0, sizeof(array) / sizeof(array[0]) - 1);
    //MergeSort(array, sizeof(array) / sizeof(array[0]));
    //CountSort(array, sizeof(array) / sizeof(array[0]));
    LSDSort(array, sizeof(array) / sizeof(array[0]));
    Print(array, sizeof(array) / sizeof(array[0]));
}

相關推薦

經典排序演算法分析及實現

一、排序概念 1. 排序：將一組雜亂無章的資料按照一定的規律組織起來，就稱為排序。 2. 資料表：待排序的資料元素的有限集合。 3. 排序碼：通常資料元素有多個屬性域，其中有一個屬性域可以用來區分元素，作為排序依據，該域即為排序碼。 * 若在資料表中各個元

常見的三種排序演算法分析及對比實現（冒泡、選擇、插入）

1. 氣泡排序      1）基本思想：           在要排序的一組數中，對當前還未排好序的範圍內的全部數，自上而下對相鄰的兩個數依次進行比較和調整，           讓較大的數往下沉，較小的往上冒。即：每當兩相鄰的數比較後發現它們的排序與排序要求相反時，就

八種經典排序演算法和java實現

文章目錄 演算法概述 演算法分類 演算法複雜度 相關概念 1.氣泡排序（Bubble Sort）

7種經典排序演算法Java程式碼實現(冒泡+選擇+插入+歸併+快排+堆排序+希爾)

氣泡排序 氣泡排序的原理是：比較兩個相鄰的元素，將值較大的元素交換到至右端（比較+移動） public static void sortMpao(int[] num) {     for(int i = 1; i < num.length; i++) {

資料結構和演算法 | 氣泡排序演算法原理及實現和優化

氣泡排序（Bubble Sort）是排序演算法裡面比較簡單的一個排序。它重複地走訪要排序的數列，一次比較兩個資料元素，如果順序不對則進行交換，並一直重複這樣的走訪操作，直到沒有要交換的資料元素為止。 氣泡排序的原理 為了更深入地理解氣泡排序的操作步驟，我們現在

資料結構和演算法 | 簡單選擇排序演算法原理及實現

選擇排序是一種非常簡單的排序演算法，就是在序列中依次選擇最大（或者最小）的數，並將其放到待排序的數列的起始位置。 簡單選擇排序的原理 簡單選擇排序的原理非常簡單，即在待排序的數列中尋找最大（或者最小）的一個數，與第 1 個元素進行交換，接著在剩餘的待排序的數列

資料結構和演算法 | 插入排序演算法原理及實現和優化

插入排序演算法是所有排序方法中最簡單的一種演算法，其主要的實現思想是將資料按照一定的順序一個一個的插入到有序的表中，最終得到的序列就是已經排序好的資料。 直接插入排序是插入排序演算法中的一種，採用的方法是：在新增新的記錄時，使用順序查詢的方式找到其要插入的位置，

排序演算法 | 希爾排序演算法原理及實現和優化

希爾排序也是一種插入排序演算法，也叫作縮小增量排序，是直接插入排序的一種更高效的改進演算法。 希爾排序因其設計者希爾（Donald Shell）的名字而得名，該演算法在 1959 年被公佈。一些老版本的教科書和參考手冊把該演算法命名為 Shell-Metzner

資料結構和演算法 | 歸併排序演算法原理及實現和優化

歸併排序（MERGE-SORT）是建立在歸併操作上的一種有效的排序演算法，該演算法是採用分治法（Divide and Conquer）的一個非常典型的應用。將已有序的子序列合併，得到完全有序的序列；即先使每個子序列有序，再使子序列段間有序。 歸併排序的原理 歸

氣泡排序演算法原理及實現（超詳細）

氣泡排序（Bubble Sort）是排序演算法裡面比較簡單的一個排序。它重複地走訪要排序的數列，一次比較兩個資料元素，如果順序不對則進行交換，並一直重複這樣的走訪操作，直到沒有要交換的資料元素為止。 氣泡排序的原理 為了更深入地理解氣泡排序的操作步驟，我們現在看一下氣泡排序的原理。 首先我們肯定有一個數組

十大經典排序演算法總結——Java實現

轉自：https://blog.csdn.net/wangqyoho/article/details/52584640#t5 引 這段時間博主逐步替換為Java的實現 //博主留 2017.9.15 //2017.10.10完成氣泡排序的修改

十大經典排序演算法 講解,python3實現

接受各位指出的錯誤 重點推薦!!! 這個網址可以看到各個演算法的執行的直觀過程,找到sort 勉強推薦這個吧,前面的幾個演算法圖解還好,後面的幾個就不好了 演算法概述 這部分內容來自這麼大牛 演算法分類 十種常見排序演算法可以分為兩大類： 非線性時間比較類排序：通過

快速排序演算法原理及實現（單軸快速排序、三向切分快速排序、雙軸快速排序）

歡迎探討，如有錯誤敬請指正 1. 單軸快速排序的基本原理 快速排序的基本思想就是從一個數組中任意挑選一個元素（通常來說會選擇最左邊的元素）作為中軸元素，將剩下的元素以中軸元素作為比較的標準，將小於等於中軸元素的放到中軸元素的左邊，將大於中軸元素的放到中軸元素的右邊，然後以當前中軸元素的位置為界，將左半部分子

經典排序演算法原理及穩定性判斷

1. 氣泡排序 原理： 將n個記錄看作按縱向排列，每趟排序時自下至上對每對相鄰記錄進行比較，若次序不符合要求（逆序）就交換。每趟排序結束時都能使排序範圍內關鍵字最小的記錄象一個氣泡一樣升到表上端的對應位置，整個排序過程共進行n-1趟，依次將關鍵字最小、

Java排序演算法分析與實現：快排、氣泡排序、選擇排序、插入排序、歸併排序（一）

轉載  https://www.cnblogs.com/bjh1117/p/8335628.html   一、概述： 　　本文給出常見的幾種排序演算法的原理以及java實現，包括常見的簡單排序和高階排序演算法，以及其他常用的演算法知識。 　　簡單排序：氣泡排序、選擇排序、

幾種經典排序演算法的JS實現方法+隨機洗牌演算法

一.氣泡排序functionBubbleSort(array) { var length = array.length; for(var i = length - 1; i > 0; i--) { //用於縮小範圍 for(var j = 0; j

八種排序演算法原理及實現

一：氣泡排序氣泡排序（Bubble Sort），是一種電腦科學領域的較簡單的排序演算法。它重複地走訪過要排序的數列，一次比較兩個元素，如果他們的順序錯誤就把他們交換過來。走訪數列的工作是重複地進行直到沒有再需要交換，也就是說該數列已經排序完成。氣泡排序演算法的運作如下：（從後

快速排序演算法思想及實現

快速排序演算法是對氣泡排序演算法的一種改進，它的核心思想就是選取一個基準元素(通常已需要排序的陣列第一個數)，然後通過一趟排序將比基準數大的放在右邊，比基準數小的放在左邊，接著對劃分好的兩個陣列再進行上述的排序。 例如對陣列5,4,1,7,3,9,21,-1進

密碼強度檢測演算法分析及實現(JavaScript)案例說明

用正則表示式做使用者密碼強度的通過性判定，過於簡單粗暴，不但使用者體驗差，而且使用者帳號安全性也差。那麼如何準確評價使用者密碼的強度，保護使用者帳號安全呢？本文分析介紹了幾種基於規則評分的密碼強度檢測演算法，並給出了相應的演示程式。大家可以根據自己專案安全性需要，做最適合於自

經典排序演算法分析

從學第一門計算機語言開始就瞭解了選擇、氣泡排序等演算法，後來又學習了高效的歸併、快速排序，排序演算法種類很多，一直都想把它們總結一下，但卻信心不足。這幾天終於下定決心嘗試寫一寫，於是看了演算法導論，在網上也查了很多資料，最終將這些排序演算法一個一個用C語言實現，