二叉搜尋樹(BST)

基礎知識

• 樹通常用來儲存已排序或已有序的資料。在樹中儲存資料，常見的就是二叉搜尋樹(Binary Search Tree，BST）
• BST中的資料是按值排序的：一個節點所有的左側子孫節點都小於或等於該節點，所有的右側子孫節點都大於或等於該節點。
• 當面試官說樹的時候，通常二叉樹，再確認是否為二叉搜尋樹
• 如果使用中序遍歷二叉搜尋樹，遍歷的順序會按照節點關鍵字的大小關係從小到大依次進行。

定義

typedef struct TreeNode 
{
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode* parent;
};
 

插入

將關鍵字k插入到二叉搜尋樹

若是已經存在，就不再插入
所以插入都是插入在葉子節點
比如已經有了5->6->9,
當插入7的時候，7並不會插入在6和9之間，而是插入在9的左邊

1. 找到要插入的位置節點，當前位置為空時
2. 新建一個節點，給其賦當前值，再使其指向當前的父節點

int BST_Insert(TreeNode *root, int k, TreeNode* parent=NULL)
{
    if(root==NULL)
    {
        TreeNode* tempNode=(TreeNode*)malloc(sizeof(TreeNode));
        tempNode->
 
val=k;
        tempNode->left=NULL;
        tempNode->right=NULL;
        tempNode->parent=parent;
        return 1;
    }
    else if(k==root->val)
        return 0;//樹中存在相同的關鍵字
    else if(k<root->val)
        return BST_insert(root->left,k,root);
    else
        return BST_insert(root->
 
right,k,root);
}

構造

用陣列arry[]建立二叉查詢樹

void create_BST(TreeNode* root,int arr[],int n){
    root=NULL;//初始為空樹
    for(int i=0;i<n;i++)
        BST_insert(root,arry[i]);
}

查詢

遞迴：

TreeNode* BST_Search(TreeNode* root,int key){
    if (root==NULL||key==root->val)
      return root;
    if (key<root->val) 
      return BST_Search(root->left,key);
    else
      return BST_Search(root->right,key);
}

非遞迴：

TreeNode* BST_Search_NonRecur(TreeNode* root, int key)
{
    while(root != NULL && key != root->val)
    {
        if(key < root->val)
            root = root->val;
        else
            root = root->val;
    }
    return T;
}

最大值與最小值

TreeNode* BST_Minnum(TreeNode* root)
{
    while(root->left != NULL)
        root = root->left;
    return root;
}
TreeNode* BST_Maxnum(TreeNode* root)
{
    while(root->right != NULL)
        root = root->right;
    return root;
}

最近共同祖先（LCA）

二叉搜尋樹的最近共同祖先(LowestCommonAncestor）
假定樹中存在這兩個點的值

檢查當前節點
If value1和value2都小於當前節點的值
   檢查左子節點
If value1 和value2 都大於當前節點的值
    檢查右子節點
否則
當前節點就是最近共同祖先

非遞迴：

TreeNode* find_LCA(TreeNode* root,int value1,int value2){
    while(root!=NULL){
        int value=root->val;
        if(val>value1&&val>value2)
            root=root->left;
        else if(val<value1&&val<value2)
            root=root->right;
        elsee
            return root;
    }
    return NULL;//only if empty tree;
}

前驅和後繼

問題：給定一個二叉查詢樹的節點，求出它在中序遍歷中的前驅和後繼。

後繼：
兩種情況

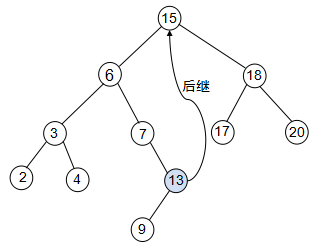
1. 若結點 x 的右子樹不為空，則 x 的後繼就是它的右子樹中關鍵字值最小的結點；
2. 若結點 x 的右子樹為空，為了找到其後繼，從結點 x 開始向上查詢，直到遇到一個祖先結點 y，它的左兒子也是結點 x 的祖先，則結點 y 就是結點 x 的後繼。如下圖

TreeNode* BST_successor(TreeNode* node){
    if(node->right!=NULL)
        return BST_Minnum(node->right);
    TreeNode* p =node->parent;
    while(p!=NULL&&p->right==node){

        node=p;
        p=p->parent;

    }
}

前驅

兩種情況

1. 若結點 x 的左子樹不為空，則 x 的前驅是它的左子樹中關鍵字值最大的結點；
2. 若結點 x 的左子樹為空，為了找到其前驅，從結點 x 開始向上查詢，直到遇到一個祖先結點 y，它的右兒子也是結點 x 的祖先，則結點 y 就是結點 x 的前驅。

TreeNode* BST_predecessor(TreeNode* node){
    if(node->left!=NULL)
        return BST_Maxnum(node->left);
    TreeNode* p=node->parent;
    while(p!=NULL&&p->left==node){
        node=p;
        p=p->parent;
    }
    return p;
}

BST的刪除

二叉查詢樹的刪除操作相對複雜一點，它要按3種情況來處理：

1.若被刪除結點z是葉子結點，則直接刪除，不會破壞二叉排序樹的性質；
2. 若結點z只有左子樹或只有右子樹，則讓z的子樹成為z父結點的子樹，代替z的位置；
3. 若結點z既有左子樹，又有右子樹，則用z的後繼（沒有左孩子）代替z（先刪除後繼結點，再將後繼的內容去替換z），而刪除後繼結點的過程就是第一種或第二種情況。

說明：第三種情況，因為z有兩個子女，所以它的後繼肯定是它右子樹中的最左邊（最小值），也就是說它的後繼要麼是葉子，要麼只有一個右孩子

void BST_delete(TreeNode* root,TreeNode* z){
    if(z->left==NULL&&z->right=NULL){

        if(z->parent!=NULL){

            if(z->parent->left==z)
                z->parent->left=NULL;
            else
                z->parent->right=NULL;
        }
        else
            root->NULL;
        free(z);
    }
    else if(z->left!=NULL&&z->right==NULL){

        z->left->parent=z->parent;//將z的左子樹的父親設為z的父親
        if(z->parent!=NULL){

            if(z->parent->left==z)
                z->parent->left=z->left;//將z父親的左孩子指向z的左子樹
            else
                z->parent->right=z->left;
        }
        else
            root=z->left;   //刪除左斜單支樹的根結點
        free(z);
    }
    else if(z->right!=NULL&&z->left==NULL){
        z->right->parent=z->parent;
        if(z->parent!=NULL){
            if(z->parent->left==z){
                z->parent->left=z->right;
            }
            else
                z->parent->right=z->right;
        }
        else
            root=z->right;  //刪除右斜單支樹的根結點
        free(z);
    }
    else{

        TreeNode* s=BST_Successor(z);
        z->val=s->val;  //後繼s的關鍵字替換為z的關鍵字
        BST_Delete(T,s);  //轉為第一或第二種情況

    }




}

對於一個高度為h的二叉查詢樹來說，刪除操作和插入操作一樣，都是O(h)

參考1

參考2

紅黑樹

二叉查詢樹回顧

由於紅黑樹本質上就是一棵二叉查詢樹，所以在瞭解紅黑樹之前，咱們先來看下二叉查詢樹。

二叉查詢樹（Binary Search Tree），也稱有序二叉樹（ordered binary tree）,排序二叉樹（sorted binary tree），是指一棵空樹或者具有下列性質的二叉樹：

• 若任意結點的左子樹不空，則左子樹上所有結點的值均小於它的根結點的值；
• 若任意結點的右子樹不空，則右子樹上所有結點的值均大於它的根結點的值；
• 任意結點的左、右子樹也分別為二叉查詢樹。
• 沒有鍵值相等的結點（no duplicate nodes）。

因為，一棵由n個結點，隨機構造的二叉查詢樹的高度為lgn，所以順理成章，一般操作的執行時間為O（lgn）.（至於n個結點的二叉樹高度為lgn的證明，可參考演算法導論 第12章 二叉查詢樹 第12.4節）。

紅黑樹概述

前面我們已經說過，紅黑樹，本質上來說就是一棵二叉查詢樹，但它在二叉查詢樹的基礎上增加了著色和相關的性質使得紅黑樹相對平衡，從而保證了紅黑樹的查詢、插入、刪除的時間複雜度最壞為O(log n)。

但它是如何保證一棵n個結點的紅黑樹的高度始終保持在h = logn的呢？這就引出了紅黑樹的5條性質：

1. 每個結點要麼是紅的，要麼是黑的。
2. 根結點是黑的。
3. 每個葉結點（葉結點即指樹尾端NIL指標或NULL結點）是黑的。
4. 如果一個結點是紅的，那麼它的倆個兒子都是黑的。
5. 對於任一結點而言，其到葉結點樹尾端NIL指標的每一條路徑都包含相同數目的黑結點。

正是紅黑樹的這5條性質，使得一棵n個結點是紅黑樹始終保持了logn的高度，從而也就解釋了上面我們所說的“紅黑樹的查詢、插入、刪除的時間複雜度最壞為O(log n)”這一結論的原因。

如下圖所示，即是一顆紅黑樹(下圖引自wikipedia： http://t.cn/hgvH1l )：

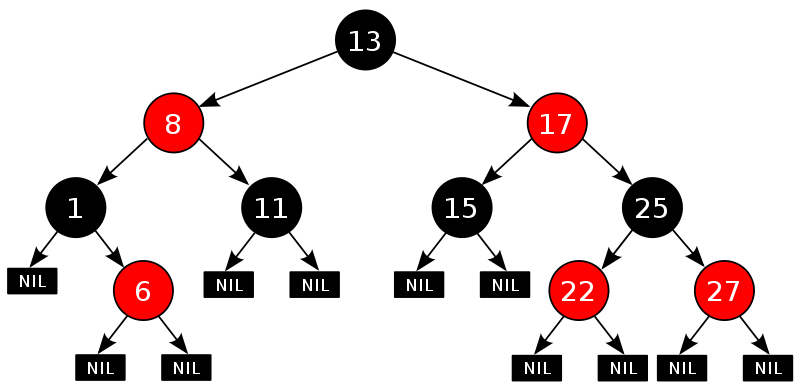
上文中我們所說的 “葉結點” 或”NULL結點”，它不包含資料而只充當樹在此結束的指示，這些結點以及它們的父結點，在繪圖中都會經常被省略。

樹的旋轉知識

當我們在對紅黑樹進行插入和刪除等操作時，對樹做了修改，那麼可能會違背紅黑樹的性質。

為了繼續保持紅黑樹的性質，我們可以通過對結點進行重新著色，以及對樹進行相關的旋轉操作，即修改樹中某些結點的顏色及指標結構，來達到對紅黑樹進行插入或刪除結點等操作後，繼續保持它的性質或平衡。

樹的旋轉，分為左旋和右旋，以下藉助圖來做形象的解釋和介紹：

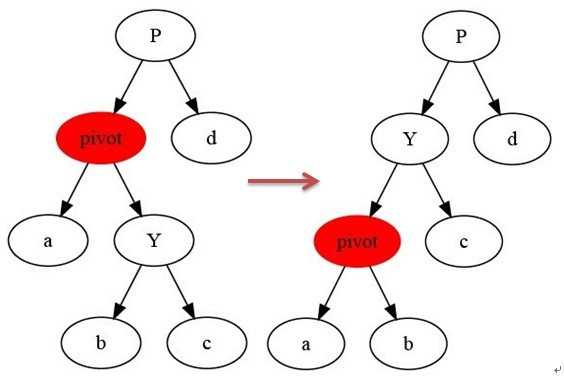
1.左旋

如上圖所示：

當在某個結點pivot上，做左旋操作時，我們假設它的右孩子y不是NIL[T]，pivot可以為任何不是NIL[T]的左孩子結點。

左旋以pivot到y之間的鏈為“支軸”進行，它使y成為該孩子樹新的根，而y的左孩子b則成為pivot的右孩子。

左旋操作的參考程式碼如下所示（以x代替上述的pivot）：

B樹

平衡樹