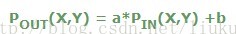學習Opencv2.4.9(三)---影象的基本運算
作者:咕唧咕唧liukun321
來自:http://blog.csdn.net/liukun321
1.影象基本運算分類及理論依據
影象的畫素級運算
1)點運算(灰度變換)——線性點運算、非線性點運算、對映表點運算
點運算特點
- 點運算針對影象中的每一個畫素灰度,獨立地進行灰度值的改變
- 輸出影象中每個畫素點的灰度值,僅取決於相應輸入畫素點的值
- 點運算不改變影象內的空間關係
- 從畫素到畫素的操作
- 點運算可完全由灰度變換函式或灰度對映表確定
例項——“對比度增強、對比度拉伸、灰度變換”
常用的線性和非線性點運算的的基礎變換函式如下圖所示:
以上可以抽象解釋為對於原影象f(x,y),灰度值變換函式T(f(x,y))
g(x,y) = T(f(x,y))
g(x,y)是目標影象
灰度變換的目的是為了改善畫質,使影象的顯示效果更加清晰。而對於彩色原影象f(x,y),顏色值變換函式
Tr(f(x,y)); Tg(f(x,y)); Tb(f(x,y));
唯一確定了非幾何變換:
gr(x,y) = Tr(f(x,y))
gg(x,y) = Tg(f(x,y))
gb(x,y) = Tb(f(x,y))
- 線性點運算變換函式及其變換後在影象上的體現:
a=1,b=0: 恆等
a<0: 黑白反轉
|a|>1: 增加對比度
|a|<1: 減小對比度
b>0: 增加亮度
b<0: 減小亮度
例如:對於取值範圍在(0,255)的灰度圖,我們可以通過令:
POUT(X,Y) = (-1)*PIN(X,Y) +255 來獲得它的負像
void linearityOpr(Mat src,Mat &dst,float slope,float intercept) { int M = 0; int N = 0; if(src.empty()){ std::cout<<"Src pic is empty\n"<<std::endl; return; } M = src.rows; N = src.cols; int j = 0; float gray = 0; for(int i = 0;i < M;i++){ for(j = 0; j < N; j++){ gray = (float)src.at<uchar>(i,j); gray = slope*((float)(1+gray)) + intercept; dst.at<uchar>(i,j) = saturate_cast<uchar>(gray); } } }
- 對於灰度對數變換的一般表示式為:
t = clog(1+s)
由對數變換的曲線特性我們可以知道,對數變換能增強影象中較暗部分的細節,從而可以擴充套件被壓縮的高值影象中較暗的畫素。因此它廣泛應用於頻譜影象的顯示。後面的opencv程式設計例項將向您展示這一特性。
void logTran(Mat src,Mat &dst,double c)
{
int M = 0;
int N = 0;
if(src.empty()){
std::cout<<"Src pic is empty\n"<<std::endl;
return;
}
M = src.rows;
N = src.cols;
int j = 0;
double gray = 0;
for(int i = 0;i < M;i++){
for(j = 0; j < N; j++){
gray = (double)src.at<uchar>(i,j);
gray = c*log((double)(1+gray));
dst.at<uchar>(i,j) = saturate_cast<uchar>(gray);
}
}
}- gamma變換。Gamma變換有常被稱為指數變換或冪變換,是一種常用的非線性變換。它的變換函式如下:
Y = (X + esp)γ
伽馬變換可以根據γ值的不同來選擇性的增強低灰度或者高灰度區域的對比度。
γ>1時,影象的高灰度區域對比度得到增強。
γ<1時,影象的低灰度區域對比度得到增強。
γ=1時,灰度線性變換,不改變原影象。
注意:gamma變換函式中 X,Y的取值範圍[0,1],因此在對影象做gamma變換前要將影象變換到0~1的動態範圍。
void gammaTran(Mat src,Mat &dst,double gamma,double comp)
{
int M = 0;
int N = 0;
if(src.empty()){
std::cout<<"Src pic is empty"<<std::endl;
return;
}
M = src.rows;
N = src.cols;
int j = 0;
double gray = 0;
for(int i = 0;i < M;i++){
for(j = 0; j < N; j++){
gray = (float)src.at<uchar>(i,j);
gray = pow((gray+comp)/255.0,gamma)*255;
dst.at<uchar>(i,j) = saturate_cast<uchar>(gray);
}
}
}- 閾值變換
void cvThreashhold(Mat src,Mat &dst,float t)
{
threshold(src,dst,255*t,255,THRESH_BINARY);
}- 分段線性變換
分段線性變換也叫做灰度線性拉伸,常用的是分三段分線性變換。實現如下:
void contrastStretch(Mat src,Mat &dst,int x1,int x2,int y1,int y2)
{
int M = 0;
int N = 0;
if(src.empty()){
std::cout<<"Src pic is empty\n"<<std::endl;
return;
}
M = src.rows;
N = src.cols;
int j = 0;
float gray = 0;
for(int i = 0;i < M;i++){
for(j = 0; j < N; j++){
gray = (float)src.at<uchar>(i,j);
if(gray <= x1){
gray = (float)(y1/x1)*gray;
}else if(gray < x2){
gray = ((float)(y2-y1)/(float)(x2-x1))*(gray-x1) + y1;
}else if(gray >= x2){
gray = ((float)(255-y2)/(float)(255-x2))*(gray-x2) + y2;
}else{
std::cout<<"Please reset the coordinate((x1,y1)or(x2,y2))\n"<<std::endl;
}
dst.at<uchar>(i,j) = saturate_cast<uchar>(gray);
}
}
}2)代數運算——加法、減法、乘法、除法
- 加法運算的定義
C(x,y) = A(x,y) + B(x,y)
主要應用舉例
去除“疊加性”噪音
生成影象疊加效果
生成影象疊加效果
對於兩個影象f(x,y)和h(x,y)的均值有:
g(x,y) = 0.5f(x,y) + 0.5h(x,y)
會得到二次曝光的效果。推廣這個公式為:
g(x,y) = αf(x,y) + βh(x,y) 其中α+β= 1
我們可以得到各種影象合成的效果,也可以用於兩張圖片的銜接
void picBlending(Mat src1 ,Mat src2,Mat &dst,double alpha,double beta,double gamma)
{
if(src1.empty()){
std::cout<<"Please set the src image"<<std::endl;
}
if(src1.rows == src2.rows&& src1.cols == src2.cols){
dst = src1.clone();
addWeighted(dst,alpha,src2,beta,gamma,dst);
}else if(src1.rows >= src2.rows&& src1.cols >= src2.cols){
Mat ROI ;
dst = src1.clone();
ROI= dst(Rect(src1.cols - src2.cols,0,src2.cols,src2.rows));
addWeighted(ROI,alpha,src2,beta,gamma,ROI);
}else if(src1.rows <= src2.rows&& src1.cols <= src2.cols){
Mat ROI ;
dst = src2.clone();
ROI= dst(Rect(src2.cols - src1.cols,0,src1.cols,src1.rows));
addWeighted(ROI,alpha,src1,beta,gamma,ROI);
} else{
std::cout<<"Couldn't blend"<<std::endl;
}
}- 減法的定義
C(x,y) = A(x,y) - B(x,y)
主要應用舉例
去除不需要的疊加性圖案
檢測同一場景兩幅影象之間的變化
- 乘法的定義
C(x,y) = A(x,y) × B(x,y)
主要應用舉例
影象的區域性顯示
用二值蒙板影象與原影象做乘法
3)邏輯運算——求反、異或、或、與
- 求反的定義
g(x,y) = R - f(x,y)
R為f(x, y)的灰度級。
主要應用舉例
獲得一個影象的負像
獲得一個子影象的補影象
- 異或運算的定義
g(x,y) = f(x,y) h(x,y)
主要應用舉例
獲得相交子影象
- 與運算的定義
g(x,y) = f(x,y) h(x,y)
主要應用舉例
求兩個子影象的相交子圖
說到代數運算,忍不住提一下opencv2:如今的opencv可以說讓我們進入了傻瓜程式設計的階段。Opencv2不僅為我們提供了更加豐富的演算法封裝,而且在很多函式的命名和操作上越來越像matlab,極大的簡化了操作(比如不用再糾結於記憶體的釋放),我們就能把更多的精力放在演算法優化而非冗雜的程式設計上!
對於算術運算這塊:Opencv2 Mat為我們過載了很多運算子,大多數的算術運算在opencv2中都有對應的過載操作符。如位操作&、|、^、~;函式min、max、abs;比較操作符< 、<=、 ==等(注意比較操作符返回的是二進位制影象)。當然它也過載了很多矩陣運算:矩陣乘法 *。另外通過Mat的成員函式也可以方便的求解矩陣求逆 inv、矩陣轉置t()、矩陣行列式等運算。這極大的簡化了程式碼的複雜度。舉一個例子,我們要獲得一幅影象的負像就可以這樣寫:
cv::Mat img = imread(“../test.jpg”,0);
img = ~img;//取反總之。。。這部分內容就先到這。。。