上章 演算法概述 中講述了 在設計演算法和比較演算法時，設計人員更傾向於假設輸入規模n無限大，然後再比較演算法的漸進效率。

為什麼要分析演算法的漸進效率，而不是直接按照輸入規模直接計算效率進行比較？

很直觀的原因就是，當輸入規模小的時候，各種演算法間的差距並不會太大，對於大部分應用程式來講，這些差距都可以被忽略。

現實原因是，要精確計算演算法執行時所消耗的資源是非常繁瑣，代價較大，甚至說不太切於實際的。

所以就有人發明了使用漸進分析法來分析演算法的漸進效率。接下來的文章我們就將根據實際的例子進行具體的分析。

但在進行演算法的漸進效率分析的時候，需要用到一些漸進符號，所以這裡實現先對之後可能用到的漸進符號進行簡單描述。

這地方可能有點比較難理解的是，漸進符號描述的表示式 表示 一個函式集合。而在漸進分析中的 ”=“更傾向於“∈ ”的意思。打個比方：漸進表示式 f(n) = O（g(n)）所表達的意思是，O(g(n)) = [ f(n),h(n).....g(n) ]; f(n) ∈ O(g(n))

一、大O表示法

      一般用於界定函式集合的上界，漸進表示式O（g（n））的含義就是，c為正常數，函式集合O中的元素的最大值不會超過c.g(n)。f(n) = O(g(n))的含義是，函式f(n)的屬於集合O（g(n)）,因為函式集合O中的最大值為c.g(n)，所以f(n)的最大值為c.g(n)。由於只是漸進的上界，所以當函式g（n）的階數越小時，上界越緊確。

      下面來看下 演算法導論 中是如何描述大O表示法的。

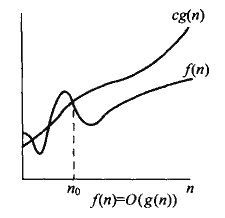
      當函式的大小隻有上界，沒有明確下界的時候，則可以使用大O表示法。f（n）= O（g（n））正式的數學定義：存在正常數c、n、n0，當n>n0的時，對於任意的f（n）對符合0<= f（n）<= c.g（n）。

      直觀視覺圖如下示：

        該漸進描述符一般用與描述演算法的最壞複雜度。讀者可以在這地方思考下，為什麼用大Ω來描述演算法的最壞複雜度沒有意義（大Ω描述的界是漸進最小，當用大Ω來描述最壞複雜度時，因為這只是一個下界，並不能說明演算法的最壞複雜度，所以沒意義）。

二、大Ω表示法

      一般用於界定函式集合的下界，漸進表示式Ω（g（n））的含義就是，函式集合Ω中的元素的最小值不會低於c.g(n)。f(n) = Ω（g（n））的含義是，函式f(n)的屬於集合Ω（g（n））,因為函式集合Ω中的最小值為c.g(n)，所以f(n)的最小值為c.g(n)。

     演算法導論 中是如何描述大Ω表示法的。     

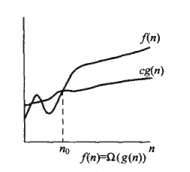
     當函式的大小隻有下界，沒有明確的上界的時候，可以使用大Ω表示法。f（n）= Ω（g（n））正式的數學定義：存在正常數c、n、n0，當n>n0的時，對於任意的f（n）對符合0<= c.g（n）<= f（n）。

     直觀視覺圖如下所示：

    該漸進描述符一般用與描述演算法的最優複雜度。讀者可以在這地方思考下，為什麼用大O來描述演算法的最優複雜度沒有意義（因為大O描述的界時漸進最大的，當你說你的演算法最快為O(f(n))的時候，因為函式描述的只是個上界，並無法描述最小值，所以沒意義）。

三、大θ表示法

       用於界定函式的漸進上界和漸進下界。當f（n）= θ（g（n））的時候，代表著g（n）為f（n）的漸進緊確界。而θ漸進描述符在所有的漸進描述符中是最嚴格的一個，因為它既描述了函式的上界，有描述了函式的下界。

       演算法導論 中是如何描述大θ表示法的。

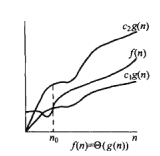
       f（n）= θ（c.g（n））正式的數學定義：存在正常數c1、c2、n、n0，當n>n0的時，對於任意的f（n）對符合c1.g（n）<= f（n）<= c2.g（n），c1.g（n）、c2.g（n）都是漸進正函式（當n趨於無窮大的時候，f（n）為正）。  

        直觀視覺圖如下所示：              

演算法導論中還根據大O，大Ω，大θ的定義得到一個定理：

當且僅當函式f（n）= O（g（n））and f（n）=Ω（g（n））時，f（n）= θ（g（n））

四、小o表示法

       剛才我們介紹了大O表示法，大O表示法所描述的界，可以是漸進緊確的，也可以是非漸進緊確的。而小o表示法所描述的界是非漸進緊確的。下面我們看下小o表示法的數學定義：

     函式f（n）= o（g（n））對於任意的正常數c，存在常數n0 > 0，使得對所有的n > n0 都存在0 <= f（n）<= c.g（n）。

      這裡可以根據定義看出同樣是0 <= f（n）<= c.g（n），大O表示法是存在一個常數c符合該條件，而小o表示法是對於所有的正常數c都符合該條件。所以當n趨於無窮大，c也趨於無窮大的時候，小o表示法描述的界的寬鬆範圍比大O表示法描述的界寬鬆範圍大最少一個次方，所以小o表示法所描述的界必然是漸進非緊確的。

五、小ω表示法

 小ω表示法和大Ω表示法的區別和小o表示法和大O表示法的區別類似。其描述的界也是漸進非緊確的。下面是小o表示法的數學定義：

     函式f（n）= o（g（n））對於任意的正常數c，存在常數n0 > 0，使得對所有的n > n0 都存在0 <= c.g（n）<=  f（n）。

函式間的特性和比較

  在後續的實際演算法分析中，會經常使用到以上五種描述符，這裡也說一下它們之間的比較關係和特性，方便以後做分析時，理解公式的推演過程。

傳遞性：

                f(n) = θ(g(n))  和 g(n) =  θ(h(n))   可以得出 f(n) =   θ(h(n))

                f(n) = O(g(n))  和 g(n) = O(h(n))   可以得出 f(n) =  O(h(n))

                f(n) = Ω(g(n))  和 g(n) = Ω(h(n))   可以得出 f(n) =  Ω(h(n))

                f(n) = o(g(n))  和  g(n) =  o(h(n))   可以得出 f(n) =  o(h(n))

                f(n) = ω(g(n))  和 g(n) = ω(h(n))   可以得出 f(n) =  ω(h(n))

       自反性： 

                f(n) = θ(f(n))     可以得出  f(n) = O(f(n))   和  f(n) = Ω(f(n))

       對稱性：

                f(n) = Θ(g(n))   當且僅當 g(n) = Θ(f(n))

       轉置對稱性：

                f(n) = O(g(n))   當且僅當 g(n) = Ω(f(n))

                f(n) = o(g(n))   當且僅當 g(n) = ω(f(n))

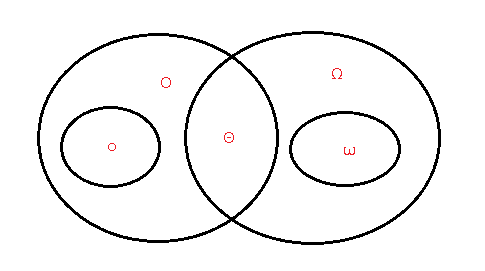
下面是關於這五種漸進符號在視覺上的直觀的比較關係：

除了這些漸進符號之外，還有一些標準記號和常用符號在演算法分析中也有遇到，不過因為其相對漸進符號來講，比較易懂，這裡就不一一贅述了，如果大家感興趣可以去 演算法導論的3.2章節自行了解下。這裡也說一下，個人感覺漸進符號在演算法分析的基礎中還是比較重要的一塊基礎知識，建議基礎較差的同學可以多看看其他的資料（書籍，帖子），自己多總結思考下，相信很快就可以掌握其中的奧祕