決策樹相關演算法——Bagging之基於CART的隨機森林詳細說明與實現
1 前言
1.1 本篇部落格主要記錄的是基於CART決策樹實現的隨機森林演算法,主要是從以下四個方面介紹: CART決策樹的構建思想;整合學習中的Bagging思想;基於CART決策樹的隨機森林程式碼實現;隨機森林不易過擬合的分析。(其中不易過擬合併不是說隨機森林不會過擬合)
1.2 本篇部落格之前的一篇部落格決策樹相關演算法——ID3、C4.5的詳細說明及實現詳細的記錄了決策樹的思想,概念及相關公式的詳解,此篇部落格便不做雷同敘述。
2 CART決策樹的構建思想
2.1 CART與ID3和C4.5的一些小差異
1.CART決策樹構建的是二叉樹,而通過ID3和C4.5演算法構建的是多叉樹。
2.CART可用於迴歸預測和分類問題, ID3和C4.5的決策樹一般來說用於分類問題。
3.CART與ID3和C4.5都是不斷特徵空間進行劃分,構建成一顆劃分特徵空間的樹。構造決策樹方式有兩點不同:
第一點,特徵選擇的方式不一樣。ID3和C4.5分別是根據資訊增益和資訊增益比選擇特徵,再根據特徵的所有特徵值劃分為多個子樹。CART分類問題中是根據Gini係數在某個特徵取某個值時候得大小進行特徵選擇和特徵值選擇。CART迴歸問題是根據最小化預測誤差(平方誤差)來進行進行特徵選擇和特徵值選擇。
第二點,特徵空間劃分的方式不一樣。ID3和C4.5選擇某個特徵劃分後,該特徵便不再參與接下來的子樹的特徵選擇劃分,最後生成的決策樹是區域性最優的,採取的貪心的思想。CART是根據某個指標(預測誤差或Gini係數)最優尋找最優特徵劃分點和最優特徵劃分值,來不斷二分特徵空間。
2.2 Sklearn中CART的實現解讀
1.from sklearn.tree import DecisionTreeClassifier 二叉分類樹
2.from sklearn.tree import DecisionTreeRegressor 二叉迴歸樹
2.2.1 類結構上分析
1.DecisionTreeClassifier與DecisionTreeRegressor都繼承BaseDecisionTree
2.BaseDecisionTree中定義好決策樹實現的結構:包括生成決策樹、使用決策樹預測資料、決策樹中的成員變數設定。#而具體如何實現交由子類決定。
#子類通過程式碼來決定是構建迴歸樹還是分類樹
super(DecisionTreeClassifier, self).__init__/.fit
super(DecisionTreeRegressor, self).__init__/.fit
3. 2.2.2 CART的生成詳解
CART的生成主要分為迴歸樹的生成和分類樹的生成。對一個多維特徵空間(即由各個特徵為維度組成的特徵空間,每一個樣本即為特徵空間中的點)的劃分——尋找特徵空間的最優特徵(維)和該特徵的取值進行二分,迴歸樹採用的是最小化平方誤差準則,而分類樹採用的是基尼係數最小化準則。
經過劃分好的特徵空間對應著R1,R2,…,RM個不同的空間區域,每一個空間區域對應著相應的預測值c1,c2,…,cm——類別或者要預測的迴歸值
如何在一個特徵空間不斷的劃分空間區域,即不斷的尋找各自的劃分點???及何時停止對特徵空間的劃分???
迴歸樹的方式——最小化平方誤差準則
平方誤差的公式為:
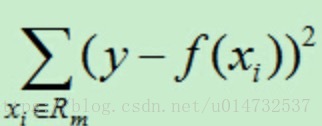
每經過一次劃分後形成的區域為兩塊,類似於切蛋糕似的劃分,其中j表示選擇劃分的特徵,在空間中即為j軸,s為j軸上的取值點:

於是對於劃分的結果就會產生一個迴歸誤差,目標就是尋找最優切分特徵j和最優切分點s使得下面式子最小:
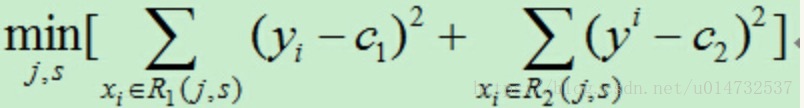
劃分步驟:
1.遍歷特徵空間中的特徵軸j,對固定的切分特徵j掃描切分點s,使上式最小。得到一個值(j,s)。
2.選定(j,s)後切分空間為R1和R2並設定響應的取值Ci取值為該區間所有yi的平均值。
3.繼續對兩個區域進行相應的切分,直至滿足停止條件(設定區間的樣本數小於設定的閾值或者均分誤差小於設定的閾值或沒有特徵可供選擇了)
4.最後生成決策迴歸樹
分類樹的方式——最小化基尼係數準則
分類樹用基尼係數選擇特徵,同時決定該特徵對應的最優二值切分點。
基尼係數的計算 上一篇部落格已經給出。遍歷特徵A,找出使Gini(D,A)最小的特徵及在特徵A上響應的取值a.作為最優劃分點。分別對左右子樹再進行查詢,直達達到停止條件(設定區間的樣本數小於設定的閾值或者均分誤差小於設定的閾值或沒有特徵可供選擇了)。
其中A=a的查詢方法是將離散型的特徵取值按順序排列,分別求出兩兩間的中值,在特徵A的基礎上遍歷中值看看那個取值a能使Gini(D,A)最小。
2.2.3 Sklearn中的CART的生成程式碼分析
#1.設定搜尋切分點J,s的最小化標準是CRITERIA_CLF/CRITERIA_REG
criterion = self.criterion
if not isinstance(criterion, Criterion):
#是二叉分類樹,CRITERIA_CLF包括gini係數
if is_classification:
criterion = CRITERIA_CLF[self.criterion](self.n_outputs_,self.n_classes_)
else:
#二叉迴歸樹,CRITERIA_REG包括mse迴歸預測誤差
criterion = CRITERIA_REG[self.criterion](self.n_outputs_,n_samples)
#2.從程式碼中可以看出尋找劃分點的程式碼被抽象出成為一個類Splitters,包含多種尋找切分點的方式 。
#Splitters are called by tree builders to find the best splits on both
splitter = self.splitter
if not isinstance(self.splitter, Splitter):
splitter = SPLITTERS[self.splitter](criterion,
self.max_features_,
min_samples_leaf,
min_weight_leaf,
random_state,
self.presort)
#3.build二叉決策樹,根據是否設定max_leaf_nodes決策樹的最大葉節點數,有兩種構建二叉決策樹的方法DepthFirstTreeBuilder深度優先樹和BestFirstTreeBuilder最佳優先樹
if max_leaf_nodes < 0:
builder = DepthFirstTreeBuilder(splitter, min_samples_split,
min_samples_leaf,
min_weight_leaf,
max_depth,
self.min_impurity_decrease,
min_impurity_split)
else:
builder = BestFirstTreeBuilder(splitter, min_samples_split,
min_samples_leaf,
min_weight_leaf,
max_depth,
max_leaf_nodes,
self.min_impurity_decrease,
min_impurity_split)
#具體構建的過程在C程式碼中實現的。python中只是呼叫了
#from /Users/jian/anaconda2/envs/python36/lib/python3.6/site-packages/sklearn/tree/_tree.cpython-36m-darwin.so這個動態庫中
builder.build(self.tree_, X, y, sample_weight, X_idx_sorted)#1.build樹程式碼的重要程式碼
while not stack.is_empty():
{
if not is_leaf:
#尋找切分點
splitter.node_split(impurity, &split, &n_constant_features)
# If EPSILON=0 in the below comparison, float precision
# issues stop splitting, producing trees that are
# dissimilar to v0.18
is_leaf = (is_leaf or split.pos >= end or
(split.improvement + EPSILON <
min_impurity_decrease))
#記錄下切分點
node_id = tree._add_node(parent, is_left, is_leaf, split.feature,
split.threshold, impurity, n_node_samples,
weighted_n_node_samples)
#將左右節點入棧,以繼續進行切分
if not is_leaf:
# Push right child on stack
rc = stack.push(split.pos, end, depth + 1, node_id, 0,
split.impurity_right, n_constant_features)
if rc == -1:
break
# Push left child on stack
rc = stack.push(start, split.pos, depth + 1, node_id, 1,
split.impurity_left, n_constant_features)
if rc == -1:
break
}建立CART的樹過程可以自行詳細瞭解。
2.2.4 CART的預測
#驗證X資料集
X = self._validate_X_predict(X, check_input)
#呼叫C中的預測函式
proba = self.tree_.predict(X)
n_samples = X.shape[0]
#判斷時分類問題還是迴歸預測
# Classification
if is_classifier(self):
#self.n_outputs是要預測的label維數
if self.n_outputs_ == 1:
return self.classes_.take(np.argmax(proba, axis=1), axis=0)
else:
predictions = np.zeros((n_samples, self.n_outputs_))
for k in range(self.n_outputs_):
predictions[:, k] = self.classes_[k].take(
np.argmax(proba[:, k], axis=1),
axis=0)
return predictions
# Regression
else:
if self.n_outputs_ == 1:
return proba[:, 0]
else:
return proba[:, :, 0]3 整合學習中的Bagging思想
3.1整合學習概述
1.簡單的說是整合學習是由多個弱分類器進行學習,將學習的結果經過某種組合策略並最終輸出要預測的值的一個過程。主要有兩點要求:弱分類器有一定的學習能力;弱分類器之間有一定的差異。
2.整合學習主要有2種組合策略:Bagging,Boosting.其中也可以瞭解下Stacking.
本篇部落格主要是使用CART作為基礎分類器,按照一定的組合策略進行整合學習實踐。
3.2 Bagging(Bootstrap aggregating)再取樣
其中Bootstrap為有放回的取樣方法。
Bootstrap aggregatinga的一般方式為:
1.從樣本集D中選出一定數量的樣本N,選完後再將這N個樣本放回,重複該取樣操作M次,得到M個數據集D1,D2,…,DM。
2.在所有特徵屬性上利用M個數據集訓練出M個弱分類器。
3.組合這M個分類器預測的結果。投票法或平均法。
其中隨機森林Random forest便屬於Bagging方式中的一種。接一下著重實現隨機森林的演算法。
3.3 Boosting提升方法
Boosting也是學習一系列弱分類器,並將其組合為一個強分類器。
Boosting的一般方式為:
1.根據初始訓練資料集訓練出基分類器。
2.根據基分類器上的表現上(誤差)上,調整訓練集的樣本權重——使之前分錯的樣本更受分類器關注,然後再對調整後的訓練集樣本和前幾個分類器加權累加組合進行訓練得到下一個分類器。
3.如此重複學習出M個分類器,最後的組合分類器便是由這M個分類器加權累加組成。
接下來幾篇部落格將詳細記錄實現Boosting的過程,此篇不再敘述。
4 基於CART決策樹的隨機森林的實現
隨機森林主要體現兩個隨機性:隨機取樣+隨機選取特徵
主要步驟:
1.從樣本集通過BootStrap方式採取n個樣本構成資料集D。
2.從所有特徵中隨機選擇K個特徵,在資料集D上訓練CART決策樹。
3.重複步驟1,2,M次,得到M個CART決策樹,於此便建立了含M個CART的決策樹的隨機森林。
4.根據這M個CART決策樹預測的結果,進行一定策略(可以是投票或者平均)的組合,得到最終結果。
說明:其中隨機採取的樣本個數n和隨機選擇的特徵數,需要根據經驗來設定。
隨機森林程式碼實現示例:
程式碼地址
# 1 匯入相關包,定義分類還是迴歸列舉型別
from sklearn.tree import DecisionTreeRegressor
from sklearn.tree import DecisionTreeClassifier
from enum import Enum
class TypeClass(Enum):
DecisionTreeClassifier_type = 1
DecisionTreeRegressor_type = 2
# 2 建立基於CART的隨機森林,主要兩個隨機取樣函式
# random.sample和dataframe.sample
def randomforst(D,N,M,K,type_class):
"""
:param D: 資料集D,格式為[Feature,label],型別為np.ndarray
:param N: 一次隨機選取出的樣本數
:param M: M個基分類器
:param k: 所有特徵中選取K個屬性
"""
D_df = pd.DataFrame(D)
D_df.as_matrix()
trees = []
for count in M:
# 隨機取樣N個樣本
D_df_i = D_df.sample(N)
# 隨機選取K個特徵
#包含label所以需要減1
feature_length = D_df.shape[0] - 1
feature_list = range(feature_length)
choice_features = random.sample(feature_list,K)
#最終的Di資料集
D_df_i_data = D_df_i[choice_features]
if isinstance(type_class,TypeClass):
if type_class == TypeClass.DecisionTreeClassifier_type:
cart_t = DecisionTreeClassifier(criterion='gini')
else:
cart_t = DecisionTreeRegressor(criterion='mse')
y = D_df_i_data[-1].as_matrix()
X = D_df_i_data.drop([-1], axis=1).as_matrix()
tree = cart_t.fit(X, y)
trees.append(tree)
else:
raise Exception('input param error')
return trees
#3 預測
def randomforst_predict(trees,test_x, type_class):
if isinstance(type_class, TypeClass):
results = []
for tree in trees:
result = tree.predict(test_x)
results.append(result)
results_np = np.array(results)
if type_class == TypeClass.DecisionTreeClassifier_type:
return get_max_count_array(results_np)
else:
return np.mean(results_np)
else:
raise Exception('input param error')
def get_max_count_array(arr):
count = np.bincount(arr)
max_value = np.argmax(count)
return max_value5 隨機森林不易過擬合的分析
前提:此處說的不易過擬合是相對於單個決策樹而言的.
過擬合:表示演算法模型在訓練資料上擬合的非常好,但是在測試的新資料上泛化能力弱。
一般來說訓練資料上的模型複雜度和誤差關係如下:
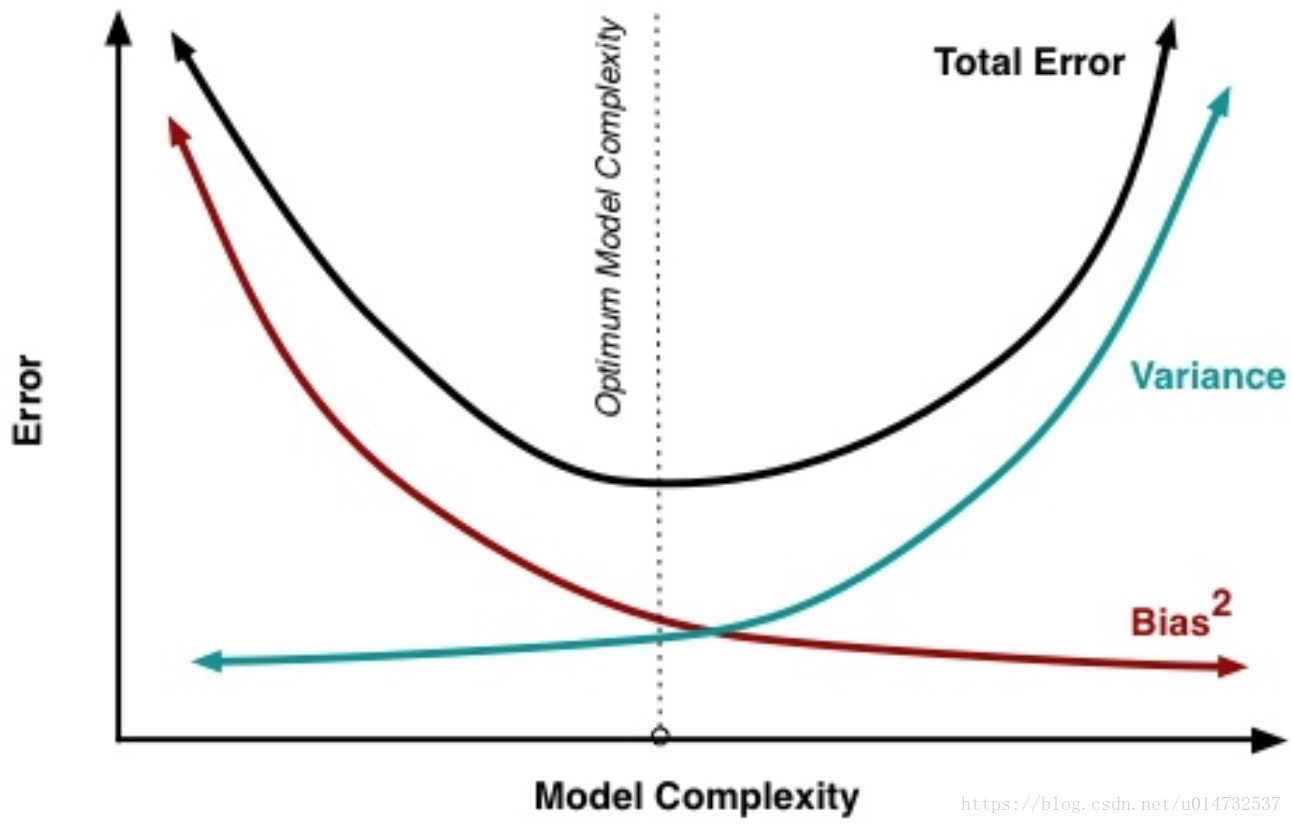
1.Bias表示偏差,可理解為模型擬合訓練資料的程度。Bias越小表示模型更擬合訓練資料。
2.Variance表示方差,可理解為模型擬合測試的新資料集的程度。Variace越大表示泛化能力越差。
3.可以看出訓練的模型越複雜,越容易發生過擬合的情況。
隨機森林有兩個隨機選擇過程:
1.所有特徵中隨機選擇部分特徵,一定程度上降低了模型分類器的複雜程度。可能又會有疑問,隨機選擇的特徵會把對label重要的特徵給漏選了,對這一點上,重複進行了M次隨機特徵選擇的構成一個由M個弱分類器的組合,這將不會使得重要的特徵給遺漏掉。
2.從總資料集上隨機選取一定數量的樣本資料,我們都知道資料集上是存在資料噪音的,這也是造成模型容易過擬合的原因,從總資料集上隨機選取一定數量的樣本資料,將在一定程度上降低資料噪音的數量。
