【時間】2018.09.18

【題目】演算法導論第三版第一章答案

一、練習1.1

練習1.1.1

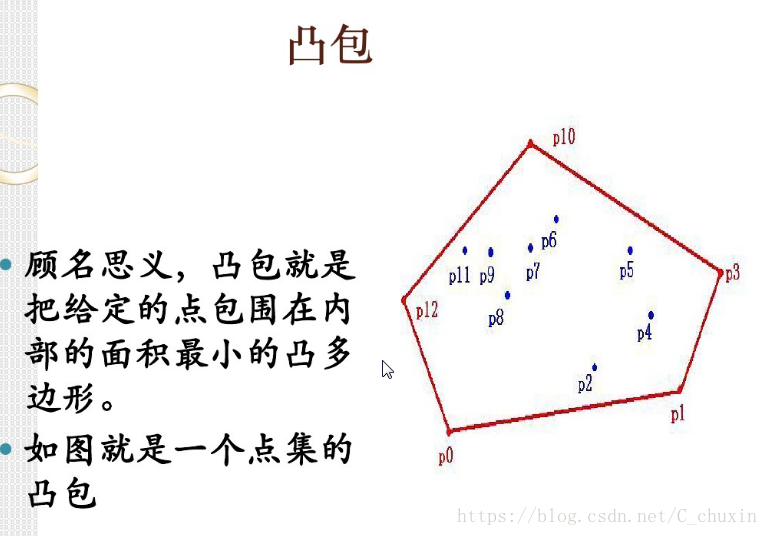
給出一個需要排序的現實示例或需要計算凸包的真實示例。

排序的真例項子非常簡單 - 例如，按字母順序呈現列表的每個網頁都需要對條目進行排序 - 目錄，索引或其他任何內容。

我不知道為什麼我們需要計算凸包，但維基百科說有很多應用程式。

【補充】：

a)排序:將一次考試中 500名考生的成績按分數從高到低迕行排名。

b)確定多矩陣相乘的最佳順序:某實驗模型,需要計算 返 17個矩陣的積,根據矩陣乘法的結合律確定計算順序,以達到計算乘法次數最少的目的。※矩陣乘法的結合律:

c)找出凸殼:木板上釘了 21個釘子,以其中一些釘子為頂點組成的凸多邊形可以包含所有 21個釘子,找出使凸多邊形達到最小的所有釘子。

練習1.1.2

除了速度之外，在現實環境中可以使用哪些其他效率指標？

記憶體使用和資源利用（網路，資料庫）是很好的答案。

練習1.1.3

選擇您之前看到的資料結構，並討論其優勢和侷限性。

我們來看看單鏈表。

優勢：

• 它不需要記憶體中的順序空間

• 我們可以在任何地方插入新元素

限制：

• 隨機訪問是O（n）

• 它需要額外的記憶體用於連結

練習1.1.4

上面給出的最短路徑和旅行商問題如何相似？他們有什麼不同？

它們是相似的，因為每個人都必須走一個圖並在其中找到一條路徑。

不同之處在於對解決方案的約束。最短路徑僅需要兩點之間的路徑，而旅行推銷員需要在返回第一點的更多點之間的路徑。

練習1.1.5

想出一個現實世界的問題，只有最好的解決方案才能解決。然後提出一個“近似”最好的解決方案就足夠了。

對目錄進行排序是一個問題，只有最佳解決方案才能實現。“近似”排序的目錄不會那麼有用。

找到一個城市中兩點之間的最短路徑是一個問題，在那裡可以做得足夠好。它可能不是最快的方式，但你仍然會到達那裡。

二、練習1.2

練習1.2.1

舉例說明在應用程式級別需要演算法內容的應用程式，並討論所涉及的演算法的功能。

在兩個地方之間找到路線時的Google地圖。

演算法是此用例的重要組成部分，因為路由是使用者最關心的。

練習1.2.2

假設我們在同一機器上比較插入排序和合並排序的實現。對於大小為n的輸入，插入排序以8n2步執行，而合併排序執行在64 nlgn步驟中。對於哪個值，插入排序優於合併排序？

在n>43處，合併排序優於插入排序。

練習1.2.3

在同一臺機器上，執行時間為100 n^2的演算法比執行時間為2^n的演算法跑得更快，那麼n的最小值是多少？

在n>14時，第一個演算法執行得更快。

三、思考題

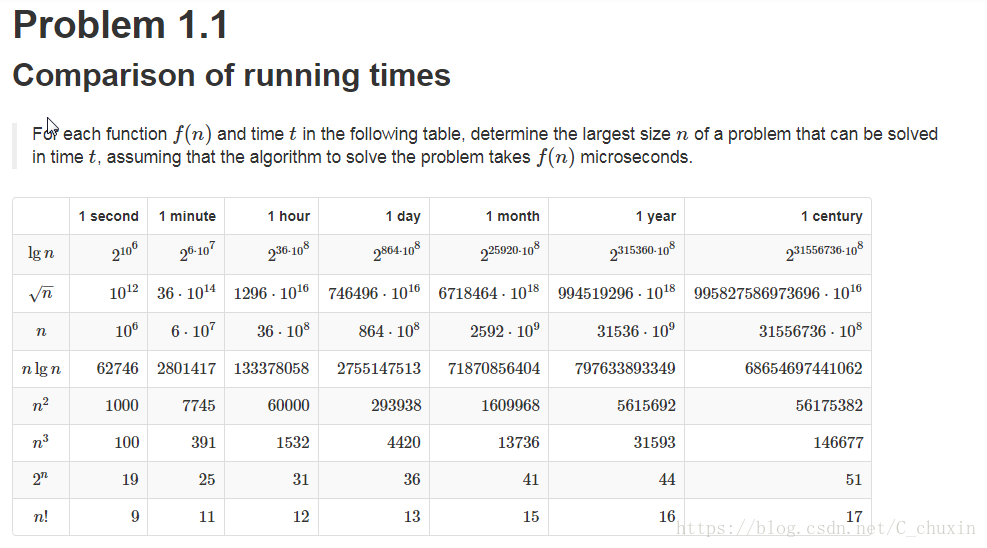
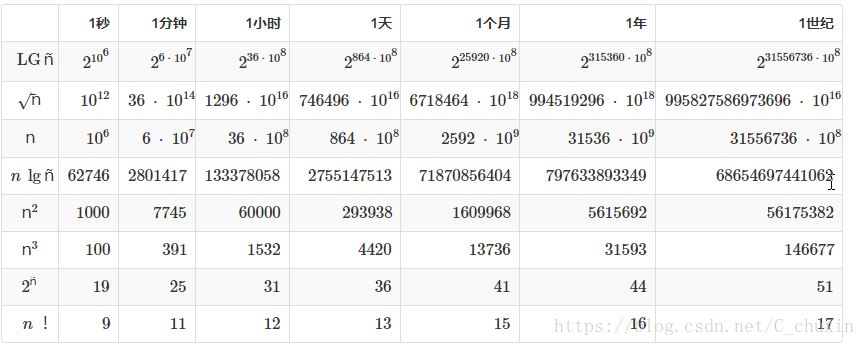
對於下表中的每個函式f(N)和時間t，確定可以在時間t中解決的問題的最大大小n，假設求解該問題的演算法需要f(N)微秒。

【PS】指數部分採用的是科學計數法