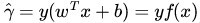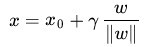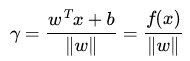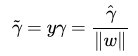而的影象是

   可以看到，將無窮對映到了(0,1)。     而假設函式就是特徵屬於y=1的概率。

當我們要判別一個新來的特徵屬於哪個類時，只需求，若大於0.5就是y=1的類，反之屬於y=0類。     再審視一下，發現只和有關，>0，那麼，g(z)只不過是用來對映，真實的類別決定權還在。還有當時，=1，反之=0。如果我們只從出發，希望模型達到的目標無非就是讓訓練資料中y=1的特徵，而是y=0的特徵。Logistic迴歸就是要學習得到，使得正例的特徵遠大於0，負例的特徵遠小於0，強調在全部訓練例項上達到這個目標。

1.1.3、形式化標示

     我們這次使用的結果標籤是y=-1,y=1，替換在logistic迴歸中使用的y=0和y=1。同時將替換成w和b。以前的，其中認為。現在我們替換為b，後面替換為（即）。這樣，我們讓，進一步。也就是說除了y由y=0變為y=-1，只是標記不同外，與logistic迴歸的形式化表示沒區別。     再明確下假設函式

    上面提到過我們只需考慮的正負問題，而不用關心g(z)，因此我們這裡將g(z)做一個簡化，將其簡單對映到y=-1和y=1上。對映關係如下：
    於此，想必已經解釋明白了為何線性分類的標準一般用1 或者-1 來標示。     注：上小節來自斯坦福機器學習課程的筆記。

1.2

、線性分類的一個例子

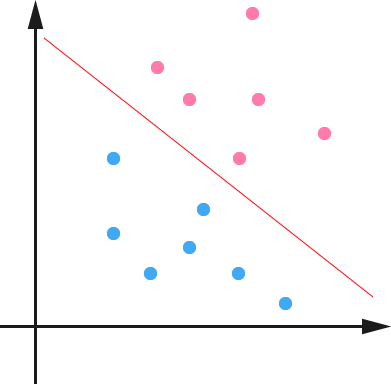
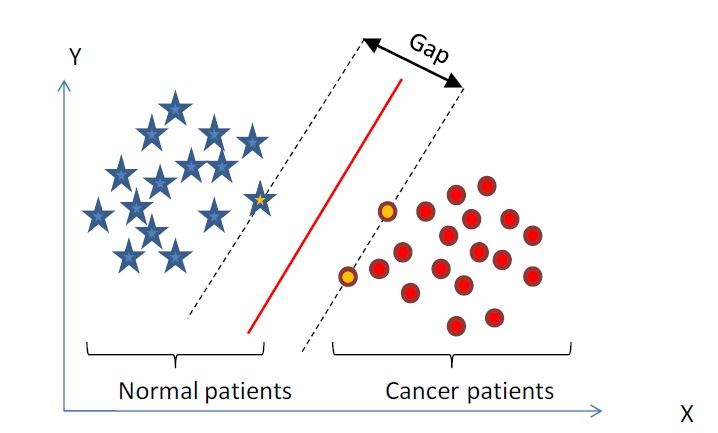
    下面舉個簡單的例子，一個二維平面(一個超平面，在二維空間中的例子就是一條直線)，如下圖所示，平面上有兩種不同的點，分別用兩種不同的顏色表示，一種為紅顏色的點，另一種則為藍顏色的點，紅顏色的線表示一個可行的超平面。

    從上圖中我們可以看出，這條紅顏色的線把紅顏色的點和藍顏色的點分開來了。而這條紅顏色的線就是我們上面所說的超平面，也就是說，這個所謂的超平面的的確確便把這兩種不同顏色的資料點分隔開來，在超平面一邊的資料點所對應的 y 全是 -1 ，而在另一邊全是 1 。

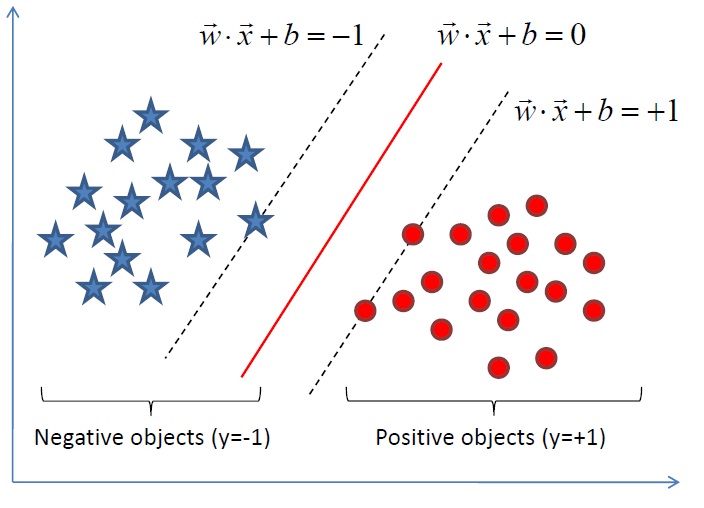
    接著，我們可以令分類函式（提醒：下文很大篇幅都在討論著這個分類函式

）：

    顯然，如果 f(x)=0 ，那麼 x 是位於超平面上的點。我們不妨要求對於所有滿足 f(x)<0 的點，其對應的 y 等於 -1 ，而 f(x)>0 則對應 y=1 的資料點。

注：上圖中，定義特徵到結果的輸出函式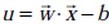，與我們之前定義的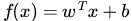實質是一樣的。為什麼？因為無論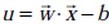是，還是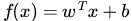，不影響最終優化結果。下文你將看到，當我們轉化到優化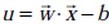的時候，為了求解方便，會把yf(x)令為1，即yf(x)是y(w^x + b)，還是y(w^x - b)，對我們要優化的式子max1/||w||已無影響。（寫成方便後面的優化演算法）     當然，有些時候，或者說大部分時候資料並不是線性可分的，這個時候滿足這樣條件的超平面就根本不存在(不過關於如何處理這樣的問題我們後面會講，把資料對映到高維空間進行處理)，這裡先從最簡單的情形開始推導，就假設資料都是線性可分的，亦即這樣的超平面是存在的。
    更進一步，我們在進行分類的時候，將資料點 x代入 f(x) 中，如果得到的結果小於 0 ，則賦予其類別 -1 ，如果大於 0 則賦予類別 1 。如果 f(x)=0，則很難辦了，分到哪一類都不是。

請讀者注意，下面的篇幅將按下述3點走：

1. 咱們就要確定上述分類函式f(x) = w.x + b（w.x表示w與x的內積）中的兩個引數w和b，通俗理解的話w是法向量，b是截距（再次說明：定義特徵到結果的輸出函式，與我們最開始定義的實質是一樣的）；
2. 那如何確定w和b呢？答案是尋找兩條邊界端或極端劃分直線中間的最大間隔（之所以要尋最大間隔是為了能更好的劃分不同類的點，下文你將看到：為尋最大間隔，匯出1/2||w||^2，繼而引入拉格朗日函式和對偶變數a，化為對單一因數對偶變數a的求解，當然，這是後話），從而確定最終的最大間隔分類超平面hyper plane和分類函式；
3. 進而把尋求分類函式f(x) = w.x + b的問題轉化為對w，b的最優化問題，最終化為對偶因子的求解。

  總結成一句話即是：從最大間隔出發（目的本就是為了確定法向量w），轉化為求對變數w和b的凸二次規劃問題。

1.3、函式間隔Functional margin與幾何間隔Geometrical margin 

    一般而言，一個點距離超平面的遠近可以表示為分類預測的確信或準確程度。

• 在超平面w*x+b=0確定的情況下，|w*x+b|能夠相對的表示點x到距離超平面的遠近，而w*x+b的符號與類標記y的符號是否一致表示分類是否正確，所以，可以用量y*(w*x+b)的正負性來判定或表示分類的正確性和確信度。

    於此，我們便引出了定義樣本到分類間隔距離的函式間隔functional margin的概念。

1.3.1、函式間隔Functional margin

    我們定義函式間隔functional margin 為： 

      接著，我們定義超平面(w，b)關於訓練資料集T的函式間隔為超平面(w，b)關於T中所有樣本點(xi，yi)的函式間隔最小值，其中，x是特徵，y是結果標籤，i表示第i個樣本，有：

  = mini  (i=1，...n)

    然與此同時，問題就出來了。上述定義的函式間隔雖然可以表示分類預測的正確性和確信度，但在選擇分類超平面時，只有函式間隔還遠遠不夠，因為如果成比例的改變w和b，如將他們改變為2w和2b，雖然此時超平面沒有改變，但函式間隔的值f(x)卻變成了原來的2倍。

    其實，我們可以對法向量w加些約束條件，使其表面上看起來規範化，如此，我們很快又將引出真正定義點到超平面的距離--幾何間隔geometrical margin的概念（很快你將看到，幾何間隔就是函式間隔除以個||w||，即yf(x) / ||w||）。

1.3.2、點到超平面的距離定義：幾何間隔Geometrical margin

    在給出幾何間隔的定義之前，咱們首先來看下，如上圖所示，對於一個點 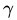x ，令其垂直投影到超平面上的對應的為 x0 ，由於 w 是垂直於超平面的一個向量，為樣本x到分類間隔的距離，我們有

              （||w||表示的是範數，關於範數的概念參見這裡）

    又由於 x0 是超平面上的點，滿足 f(x0)=0 ，代入超平面的方程即可算出：

γ

（有的書上會寫成把||w|| 分開相除的形式，其中，||w||為w的二階泛數）

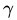
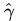
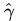
不過這裡的是帶符號的，我們需要的只是它的絕對值，因此類似地，也乘上對應的類別 y即可，因此實際上我們定義幾何間隔geometrical margin 為(注：別忘了，上面的定義，=y(wTx+b)=yf(x) )：

    （代人相關式子可以得出：yi*(w/||w|| + b/||w||)）

函式間隔y*(wx+b)=y*f(x)實際上就是|f(x)|，只是人為定義的一個間隔度量；而幾何間隔|f(x)|/||w||才是直觀上的點到超平面距離。

    想想二維空間裡的點到直線公式：假設一條直線的方程為ax+by+c=0,點P的座標是(x0,y0)，則點到直線距離為|ax0+by0+c|/sqrt(a^2+b^2)。如下圖所示：
                                 
    那麼如果用向量表示，設w=(a,b),f(x)=wx+c,那麼這個距離正是|f(p)|/||w||。

1.4、最大間隔分類器Maximum Margin Classifier的定義

    於此，我們已經很明顯的看出，函式間隔functional margin 和 幾何間隔geometrical margin 相差一個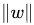的縮放因子。按照我們前面的分析，對一個數據點進行分類，當它的 margin 越大的時候，分類的 confidence 越大。對於一個包含 n 個點的資料集，我們可以很自然地定義它的 margin 為所有這 n 個點的 margin 值中最小的那個。於是，為了使得分類的 confidence 高，我們希望所選擇的超平面hyper plane 能夠最大化這個 margin 值。

    通過上節，我們已經知道：

1、functional margin 明顯是不太適合用來最大化的一個量，因為在 hyper plane 固定以後，我們可以等比例地縮放 w 的長度和 

相關推薦

如何更好的理解SVM演算法

 而的影象是    可以看到，將無窮對映到了(0,1)。     而假設函式就是特徵屬於y=1的概率。 當我們要判別一個新來的特徵屬於哪個類時，只需求，若大於0.5就是y=1的類，反之屬於y=0類。

從身邊開源開始學習，用過才能更好理解程式碼

2015年12月20日，雲棲社群上線。2018年12月20日，雲棲社群3歲。 阿里巴巴常說“晴天修屋頂”。 在我們看來，寒冬中，最值得投資的是學習，是增厚的知識儲備。 所以社群特別製作了這個專輯——分享給開發者們20個彌足珍貴的成長感悟，50本書單。 多年以後，再回首2018-19年，留給我們自己的，

雲棲專輯 | 阿里開發者們的第3個感悟：從身邊開源開始學習，用過才能更好理解程式碼

2015年12月20日，雲棲社群上線。2018年12月20日，雲棲社群3歲。 阿里巴巴常說“晴天修屋頂”。 在我們看來，寒冬中，最值得投資的是學習，是增厚的知識儲備。 所以社群特別製作了這個專輯——分享給開發者們20個彌足珍貴的成長感悟，50本書單。 多年以後，再回首2018-19年，留給我們自

更好理解貝葉斯定律(Bayes Law)和卡曼濾波器(Kalman Filter)原理

在概率理論中，我們都學習過 貝葉斯理論： P(A|B) = P(A)P(B|A) / P(B)。它的意義在模式識別和卡曼濾波中是基礎。理解它，是學習高階演算法的前提。至於模式識別和卡曼濾波等很有價值的

結合舞蹈更易理解的演算法--氣泡排序演算法[java程式碼]

舞蹈地址：http://t.cn/hrf58M 氣泡排序演算法java程式碼： /** * 氣泡排序 * @author hsy * */ public class BubbleSort { private long[] a; private in

怎麼更好地終極理解遞迴演算法【轉】

遞迴真是個奇妙的思維方式。對一些簡單的遞迴問題，我總是驚歎於遞迴描述問題和編寫程式碼的簡潔。但是總感覺沒能融會貫通地理解遞迴，有時嘗試用大腦去深入“遞迴”，層次較深時便常產生進不去，出不來的感覺。這種狀態也導致我很難靈活地運用遞迴解決問題。有一天，我看到一句英文：“To

更好的理解position:relative的應用

單元 設置 .com 證明 去掉 註意 -1 src 實例 先記錄一下問題。在使用iview的表格進行左右兩列固定時，iview會自己在傳過去的高度上加上一個滾動條的高度，如果有出現橫向滾動條還好，但是如果沒有出現橫向滾動條就會這樣 如果項目中公用樣式文件還很巧的把ivi

教你如何使用理解 懶 Redis 是更好的 Redis

大量 rep 遊標 聚合數據 memcached 是個 智能 選擇 sadd 前言大家都知道 Redis 是單線程的。真正的內行會告訴你，實際上 Redis 並不是完全單線程，因為在執行磁盤上的特定慢操作時會有多線程。目前為止多線程操作絕大部分集中在 I/O 上以至於在不同

如何讓搜尋引擎更好地理解我們想要什麼

能否有效地利用搜索引擎，對我們能否在海量資訊中迅速挖掘出所需有著決定性影響。 本文的源起是今天讀完的一本谷歌前高管寫的書《 Google 時代的工作方法》，其中一章提到對於關於谷歌搜尋的高效運用，加之先前看過為數不少的關於搜尋引擎運用的文章，結合自己平時的搜尋習慣，出於更好地理解和運用的目的，方有此文。 本

何愷明大神的「Focal Loss」，如何更好地理解？

轉自：http://blog.csdn.net/c9Yv2cf9I06K2A9E/article/details/78920998   作者丨蘇劍林 單位丨廣州火焰資訊科技有限公司 研究方向丨NLP，神經網路 個人主頁丨kexue.fm   前言

【中文分詞系列】 8 更好的新詞發現演算法

分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！        

區塊鏈100講：理解 Web 3-描述新一代更好的網際網路

通用標準和新工程帶來的網路效應 因特網又變了。 在過去的幾十年裡，基於網際網路的服務朝著中心化的方向發展。今天，那少數幾個大公司，掌握著我們用於資訊搜尋、儲存個人資料、管理個人線上身份、公開或祕密交流的平臺。 同時，一些看起來不相關的邊緣科技正在發展，包括從加密資訊到數字貨

通過一個“印表機”例子來更好的理解什麼是多型。

/** * Machine類代表一臺印表機。這臺印表機裡面分別裝有墨盒（BoxDemo類），紙張（PaperDemo類） * 這個Machine類（印表機）的構造方法是傳遞兩個引數，分別是墨盒（BoxDemo類），紙張（PaperDemo類）。 * 墨盒（Box類）也有兩個子類，彩色墨

【資訊科技】【2006.12】人工耳蝸在噪聲環境中更好地識別旋律並改善語音理解的訊號處理策略

本文為美國德克薩斯大學達拉斯分校（作者：KALYAN S. KASTURI）的電子工程碩士論文，共194頁。 人工耳蝸是由植入電極和訊號處理器組成的裝置，設計用於恢復深度耳聾人群的部分聽力。自上世紀70年代初人工耳蝸誕生以來，逐漸得到廣泛普及，因此已經進行了大

盤點｜最實用的機器學習演算法優缺點分析，沒有比這篇說得更好了

AI技術年度盛會即將開啟！11月8-9日，來自Google、Amazon、微軟、Facebook、LinkedIn、阿里巴巴、百度、騰訊、美團、京東、小米、位元組跳動、滴滴、商湯、曠視、思必馳、第四正規化、雲知聲等企業的技術大咖將帶來工業界AI應用的最新思維。 如果你是某

【轉】非常好的理解遺傳演算法的例子

非常好的理解遺傳演算法的例子 個人分類： 演算法 為更好地理解遺傳演算法的運算過程，下面用手工計算來簡單地模擬遺傳演算法的各     個主要執行步驟。         例：求下述二元函式的最大值：     (1) 個體編碼            遺傳演算法的運算物件

C語言——經典的兩個數互換的程式——更好的理解指標！！！

# include<stdio.h> int main(void) { void huhuan(int ,int); void huhuan_1(int *,int *);

比較：是為了更好的理解它的特性

我們學習一個東西時，如果能夠找到和它對標的一個東西來對比著理解和學習， 那麼，很有助於你的記憶和理解。對比是常用的一種深化記憶和理解的工具。 比如，如果你之前通過並瞭解MySQL， 那麼當你學習hb

一些簡單的例子讓你在Java中能更好的學習並理解迴圈結構（1）！

一、java中流程控制方式採用三種基本流程結構：順序結構，選擇(分支)結構，迴圈結構。   1、[if-else 結構]    if(1>2){     system.out.println("if條件成立時，執行的程式碼");   }else{     System.out.println("if條

更好的理解分析深度卷積神經網路

深度卷積神經網路（CNNs）在特徵識別相關任務中取得的效果，遠比傳統方法好。因此，CNNs常用於影象識別、語音識別等。但是，因為CNNs結構龐大，一般都會包含幾十個神經層，每一層，又有數百至數千個神經元；同時，CNNs任意兩層之間神經元的相互影響錯綜複雜。這兩個主要的因素，導致CNNs難以理解、分析。為此