Deep Residual Network學習(一)
1.論文解讀
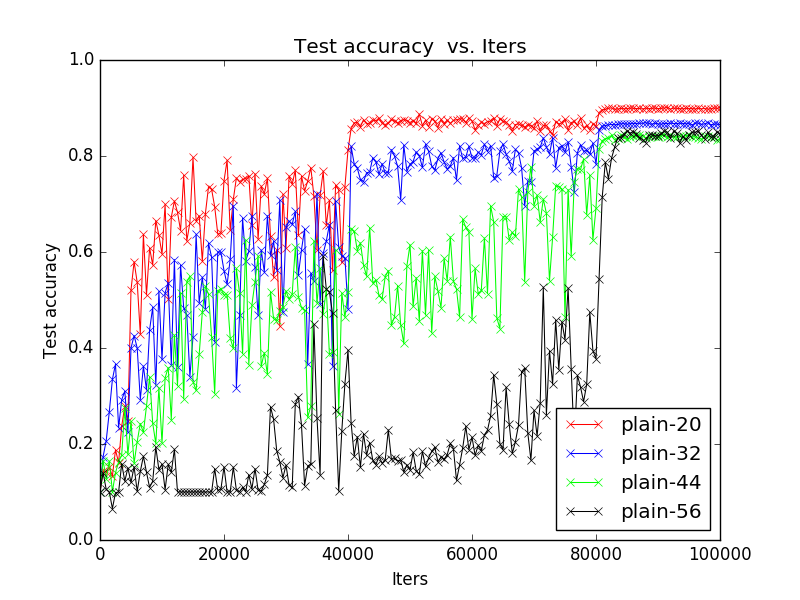
He首先提出一個問題:Is learning better networks as easy as stacking more layers?回答這個問題的一個障礙在於一個著名的問題:梯度消失/爆炸,然而這個障礙可以通過合理的初始化和其他一些技術來解決,接下來看一張圖:
這是我在論文結果復現時在CIfar10上覆現的訓練過程圖,plain-20代表不含殘差結構的純粹的20層的網路結構,很明顯可以看出隨著網路深度增加,performance卻在下降。He將這一現象稱為degradation,亦即隨著網路深度的增加,準確度飽和並且迅速減少。這一問題廣泛存在於深層的網路結構中,例如VGG的論文中也觀察到這一現象。degradation表明不是所有的系統都能很容易地被優化。
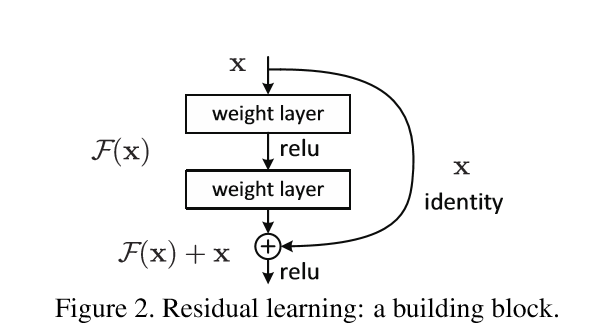
接下來,He提出了深度殘差學習的概念來解決這一問題。首先我們假設我們要求的對映是H(x),通過上面的觀察我們意識到直接求得H(x)並不那麼容易,所以我們轉而去求H(x)的殘差形式F(x)=H(x)-x,假設求F(x)的過程比H(x)要簡單,這樣,通過F(x)+x我們就可以達到我們的目標,簡單來說就是下面這幅圖,我們將這個結構稱之為一個residual block。
相信很多人都會對第二個假設有疑惑,也就是為什麼F(x)比H(x)更容易求得,關於這一點,論文中也沒有明確解釋。但是根據後面的實驗結果確實可以得到這一個結論。
“Our deep residual nets can easily enjoy accuracy gains from greatly increased depth, producing results substantially better than previous networks.”
這裡放上Kaiming大神論文中的一句話,大家自行感受即可...
2.網路結構
接下來讓我們關注一下ResNet的網路結構:
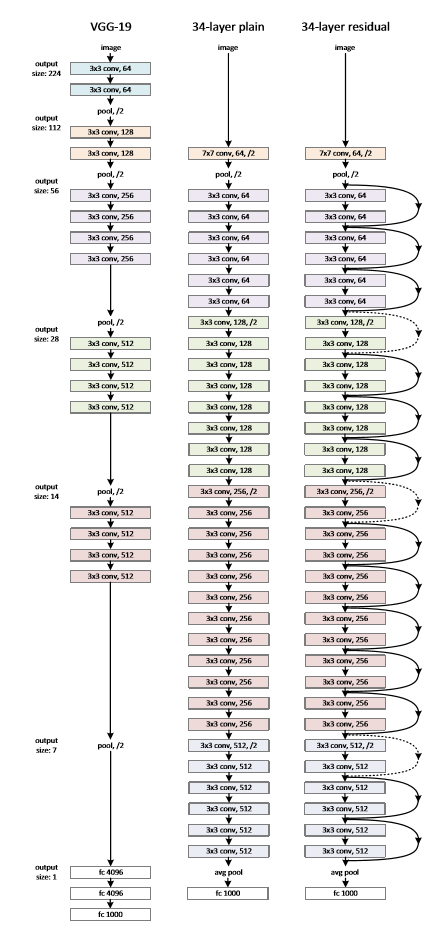
PlainNet結構主要基於VGG修改而得到,接下來我們重點關注ResNet結構。可以發現,主要結構與PlainNet一致,只是多了許多shortCut連線,可以發現,通過shortcut,整個ResNet就可以看成是許多個residual block堆疊而成。這裡值得注意的是虛線部分,虛線部分均處於維度增加部分,亦即卷積核數目倍增的過程,這時進行F(x)+x就會出現二者維度不匹配,這裡論文中採用兩種方法解決這一問題(其實是三種,但通過實驗發現第三種方法會使performance急劇下降,故不採用):
A.zero_padding:對恆等層進行0填充的方式將維度補充完整。這種方法不會增加額外的引數
B.projection:在恆等層採用1x1的卷積核來增加維度。這種方法會增加額外的引數
3.結果復現
暫時還沒有在ImageNet上覆現ResNet結果,因為太耗時了喂,聽師兄說152層的ResNet在ImageNet12上要跑一個月:(,等以後有時間在嘗試吧。接下來的部分均是ResNet在Cifar10上的復現結果,所有的實驗都是在caffe上完成的。
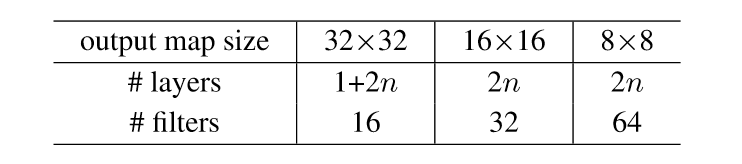
依據論文中結構,所有的卷積核都是3x3的,依據上表總共是6n+2層,n代表residual block的數目。注意:在論文中cifar10上對所有的恆等層均採用A方法,但由於caffe暫時不支援zero_padding,所以在本文中結果均採用B方法。A方法我最終也進行了復現,但這需要向caffe中新增新層,留待下次再寫吧。
資料預處理部分論文中採取對影象各邊擴充套件4個pixels的方式,亦即將32x32影象擴充套件成40x40的影象,訓練時再隨機crop一個32x32的部分進行訓練,但這裡暫時沒有進行這個操作,因為剛開始對CV的很多操作還不是很熟悉,所以採取了原始的32x32的影象擷取28x28影象的方式。
接下來就是一些訓練引數的設定了,如下:
weight_decay=0.0001momentum=0.9
batch_size=100
learning_rate=0.1,0.01/40k,0.001/80k
max_iter=100k
接下來就是實驗的結果圖了:
先是PlainNet,下面一張是限制y軸取值後得到的細節圖片,很明顯可以看出degradation問題:隨著網路層數的增加,accuracy不增反降
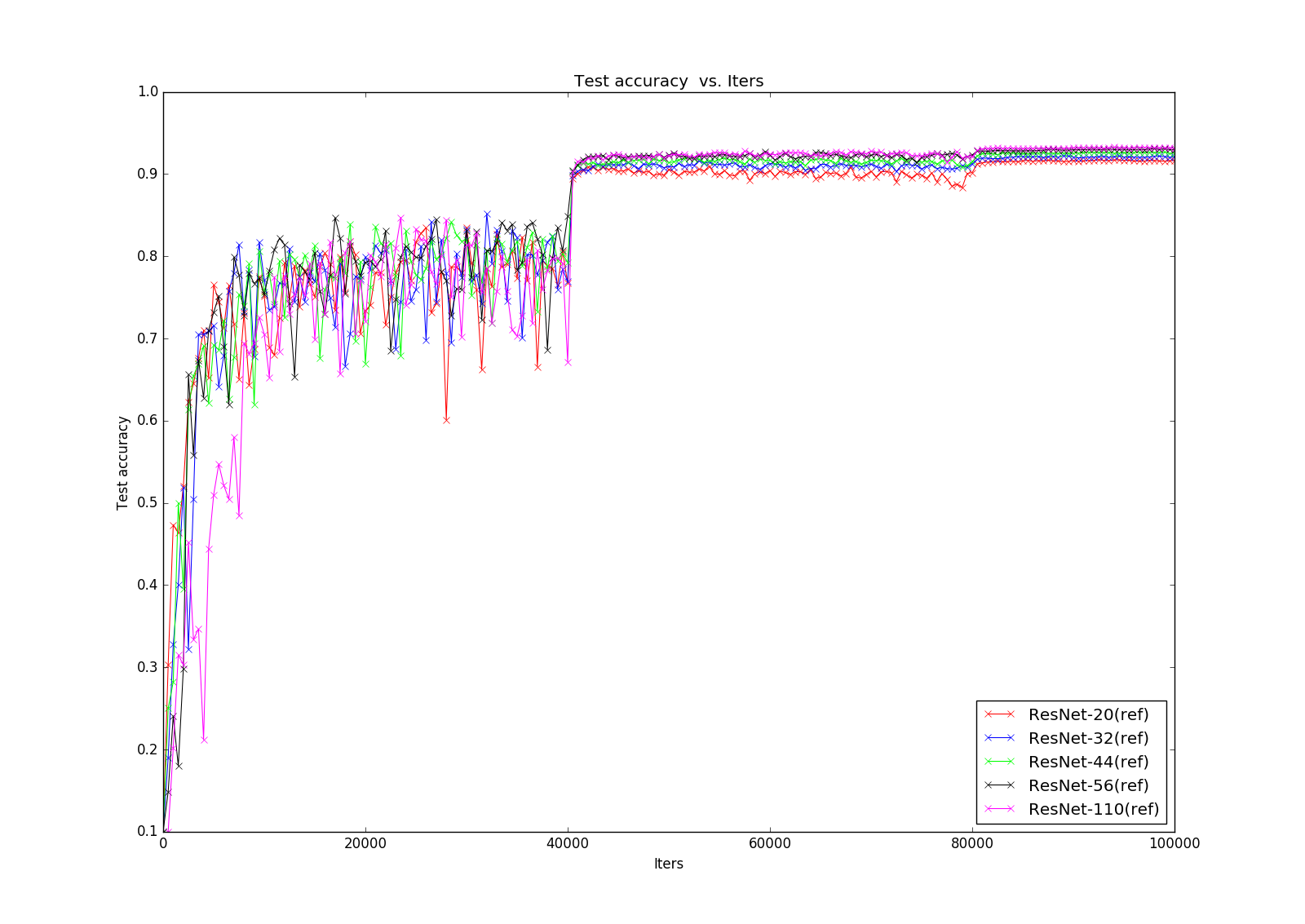
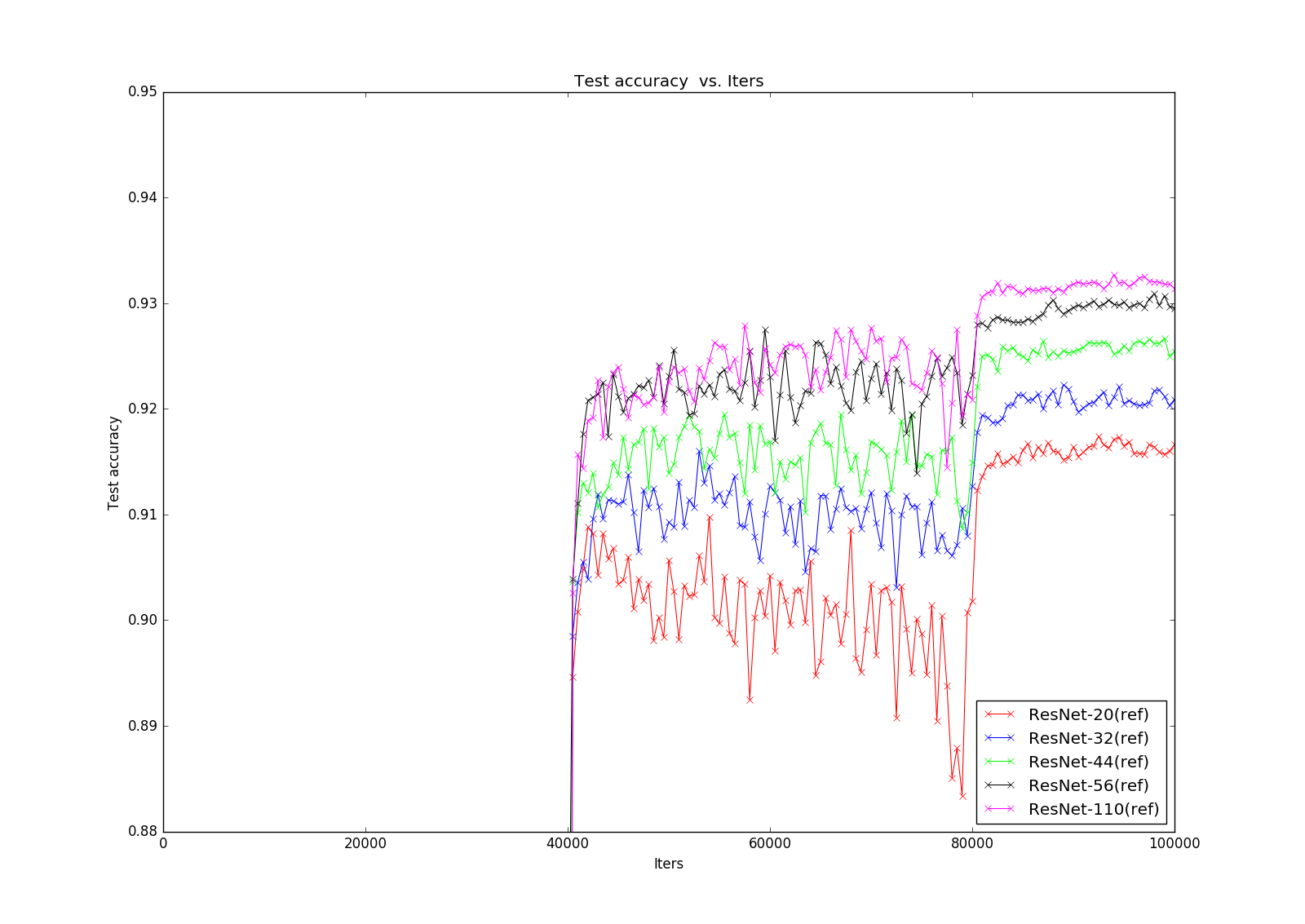
接下來就是萬眾矚目的ResNet了,上面的那張圖可能不太清楚,可以看一下下面的細節圖,這時候可以明顯看出residual block的威力了,解決了degradation的問題,這樣我們可以充分享受深度深度帶來的perfomance的提升!
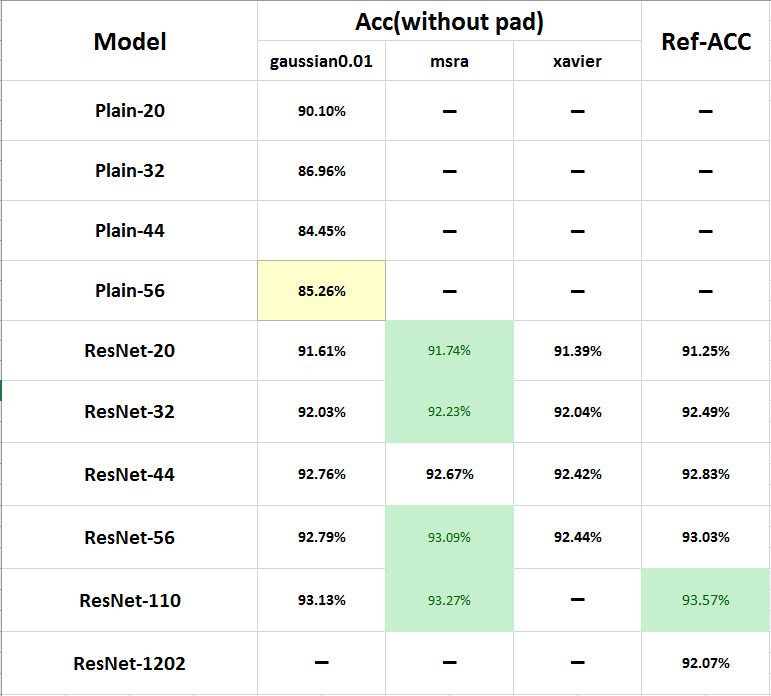
下面放一張我前期所有實驗所得到的結果表:PlainNet明顯顯現出degradation的問題,下面我們重點看ResNet,這裡我實驗了三種初始化方法,第一種是均值為0,標準差為0.01的高斯分佈,第二種是論文中所使用的初始化方法,亦即msra方法(https://arxiv.org/abs/1502.01852),第三種就是xavier了,可以看出:
1.對三種初始化方法,隨著深度增加,accuracy均得到提升
2.msra的初始化方法能達到最佳甚至超過論文中的結果
4.分析與後續
一.首先是前面提到的,在這裡的復現並沒有使用pixel padding的資料增強方法,卻達到了接近甚至超過論文中結果的performance,難道是源於我們在恆等層使用了B方法而論文中使用了A方法嗎?答案是yes,後續會有進一步分析驗證。
二.網路結構中採用了batch normalization,這個層的作用是什麼?從上述可以看出,msra初始化方法要由於其他兩種,為什麼?這些都會在後續給出分析
三.後面還將給出另一篇文章的解讀(https://arxiv.org/abs/1603.05027),實驗其中的pre-activation和bottleneck結構
四.由於caffe結構限制,即使採用了多GPU,最終也只實驗到164層的網路,對於上千層的網路則實在是沒辦法跑起來,希望有成功復現的人能給一點建議,感激不盡!