【動態規劃】LCS演算法:求兩字串最大公共字串(連續)
阿新 • • 發佈:2019-02-16
LCS演算法的應用
問題描述:求兩字串的連續最大公共子字串
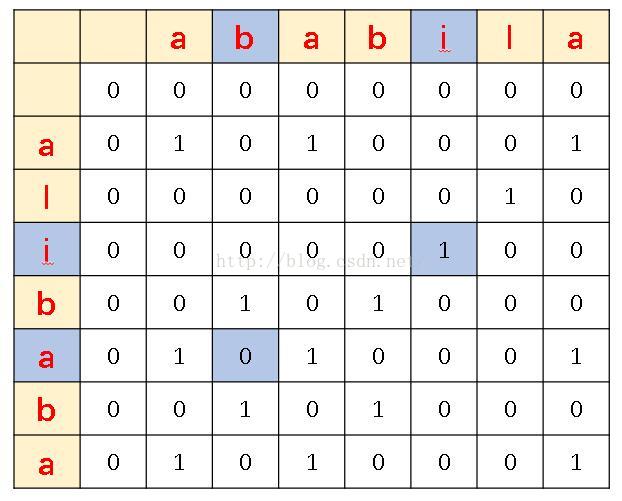
思路:根據上文LCS演算法求解兩字串的最大公共子序列(不連續),可以得到求解連續子字串的啟示,如圖所示,構造LCS矩陣vec,將兩個字串按矩陣方式排開,矩陣中的每個元素vec[i][j]表示字串a的第i個字元和字串b的第j個字元是否相等。如圖1中所示。在斜對角線上,連續的1就表示兩字串對應位置連續相等。
最長的連續1就表示該子字串是最大公共子字串。分別找出對應的字元即可求出這個最長子串。如下圖1,有兩個最長的公共子字串。bab與aba.
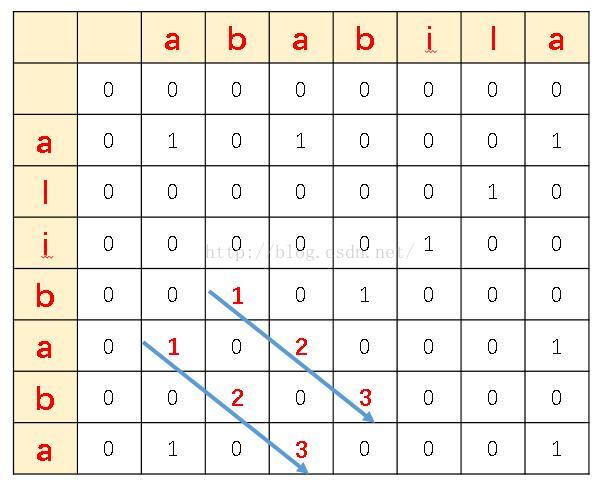
我們可以對這個演算法進行改進,當前行列相等時,在其左上角值的基礎上+1,這樣就記錄了連續1的長度,如下圖2
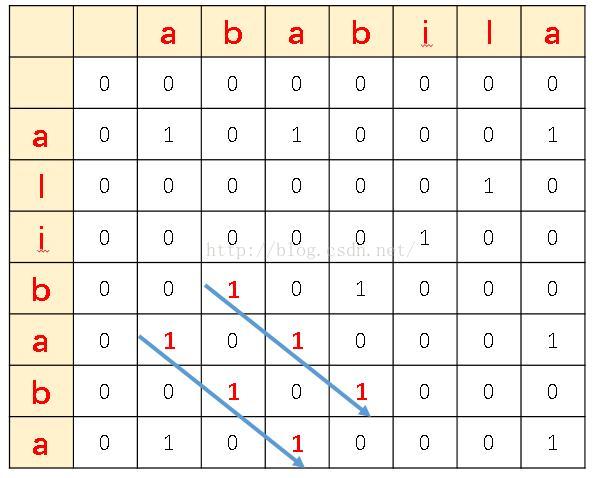
再對演算法進行改進,可以發現,我們只需要知道最大值就知道最大公共子串的長度,而最大值的位置可以求出最大公共子串的結束位置,而求解這兩個資訊,使用一個矩陣是十分浪費空間的!實際上只需要一維陣列即可解決,在求當前行時,記錄上一行的值,並始終儲存最大值所在的位置(行或列),就可以求出結果。
程式碼如下:
相關參考:string LCS_continuous(string str1,string str2) { int i,j,maxnum=0,maxj=0; int n1=str1.size(),n2=str2.size(); vector<int> last,cur,temp;//last、cur記錄上一行、當前行的LCS資訊,temp作為輔助陣列。 for(i=0;i<n2+1;i++)//初始值:第0行第0列置0 { last.push_back(0); cur.push_back(0); } temp=cur; for(i=1;i<=n1;i++) { cur=temp;//cur清零 for(j=1;j<=n2;j++) { if(str1[i-1]==str2[j-1]) { cur[j]=last[j-1]+1; if(cur[j]>maxnum)//更新最大值 { maxnum=cur[j]; maxj=j-1;//記錄最大值列號 } } } last=cur;//把當前行資訊傳遞給last } return str2.substr(maxj-maxnum+1,maxnum); }
http://blog.csdn.net/yebanxin/article/details/52186706
http://www.2cto.com/kf/201410/346523.html