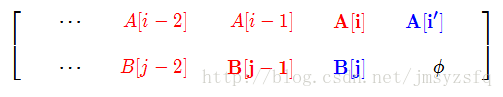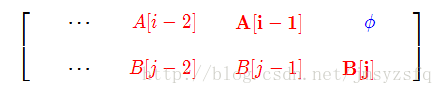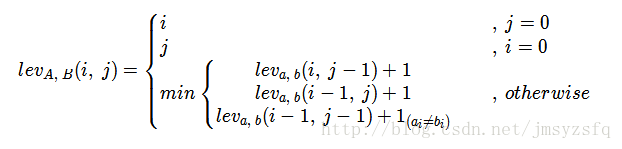基本介紹

Levenshtein距離是一種計算兩個字串間的差異程度的字串度量（string metric）。我們可以認為Levenshtein距離就是從一個字串修改到另一個字串時，其中編輯單個字元（比如修改、插入、刪除）所需要的最少次數。俄羅斯科學家Vladimir Levenshtein於1965年提出了這一概念。

簡單例子

從字串“kitten”修改為字串“sitting”只需3次單字元編輯操作，如下：

• sitten ( k -> s )
• sittin ( e -> i )
• sitting ( _ -> g )

因此“kitten”和“sitting”的Levenshtein距離為3。

實現思想

　　如何程式設計實現這一演算法呢？許多人試圖用矩陣來解釋，但實際上矩陣是最終視覺化的工具，配合理解“為什麼”比較方便，但從矩陣卻比較難想到“怎麼做”。

　　我們試圖找到“從字串A修改到字串B”這一問題的子解結構。當然反過來說“從字串B修改到字串A”和它是同一個問題，因為從A中刪掉一個字元來匹配B，就相當於在B中插入一個字元來匹配A，這兩個操作是可以互相轉化的。

　　假設字元序列A[1…i]、B[1…j]分別是字串A、B的前i、j個字元構成的子串，我們得到一個子問題是“從字串A[1…i]修改到字串B[1…j]”：

① 插入操作：

當將]A[1…i]修改成B[1…j−1]需要運算元為op1，那麼我插入一個字元A[i’]=B[i]到A[i]和A[i+1]之間，用以匹配B[i]，於是A[1…i]修改到B[1…j]所需運算元為op1​​ +1。

② 刪除操作：

當將A[1…i−1]修改成B[1…j]需要運算元為op2 ，那麼我刪掉字元A[i]也可以op​2​​ +1的運算元使兩個子字串匹配：

③ 修改操作：

如果A[1…i−1]修改成B[1…j−1]所需運算元為op​3​​ 的話，我將字元A[i]A[i]替換成A[i​′]=B[j]，就可以op​3​ +1的運算元完成：

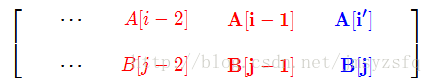
但如果此時字元A[i]==B[j]的話，則不需要進行修改操作，運算元仍為op​3​​ 。
　　綜上所述，我們將字串A[1…i]修改成字串B[1…j]所需操作為min { op​1​ +1, op​2​​ +1, op​3​​+1​(a​i​​ ≠b​i​​ )​​ }，其中1​(a​i​​ ≠b​i​​ )​​ 代表當a​i​​ ≠b​i​​ 時取值1，否則取值為0。

數學定義

　　數學上，我們定義兩個字串A和B間的Levenshtein距離為levA, B​​ (a, b)，其中a、b分別為字串A、B的長度，而

程式碼

這題思路明白了，程式碼自然就會寫了（事實上程式碼也很短）

#include <bits/stdc++.h>
#define max(x,y) (x>y?x:y)
#define min(x,y) (x<y?x:y)
using namespace std;
char a[1005],b[1005];
int f[1005][1005],n,m;
int main(){
    scanf("%s%s",a+1,b+1);
    n=strlen(a+1);m=strlen(b+1);
    int w=max(n,m);
    for(int i=1;i<=w;++i)f[i][0]=f[0][i]=i;
    for(int i=1;i<=n;++i){
        for(int j=1;j<=m;++j){
            if(a[i]==b[j])f[i][j]=f[i-1][j-1];
            else f[i][j]=min(f[i][j-1],min(f[i-1][j],f[i-1][j-1]))+1;
        }
    }
    printf("%d",f[n][m]);
    return 0;
}