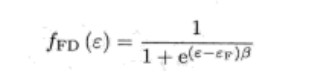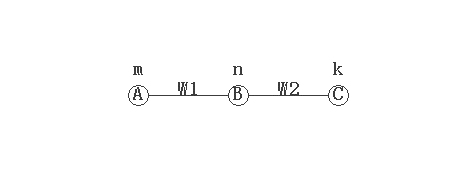
假設在m,n,k位置上有三個球A，B，C

現在讓A撞向B，同時也讓C撞向B，無論這三個小球是如何相互作用的，不管是強相互作用，弱相互作用，電磁力，或者是引力，也不管作用方向，作用力的大小，總之這兩次碰撞的結果都可以用B球在n點出現概率的變化來表示，B球在n點出現的概率w3=w1+w2

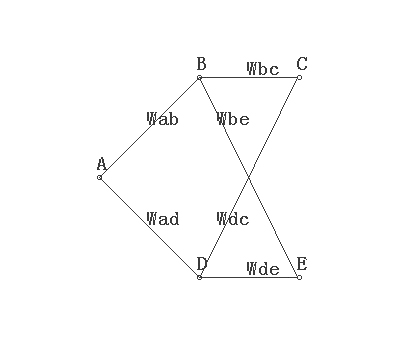
製作一個簡單1*2*2的神經網路，B點的輸入很顯然是A*Wab，按照波動力學，概率幅和電子電荷相乘就代表了電荷在空間的實際分佈，把A看作電荷，Wab是歸一化的權重當然也可以看作是概率幅，A*Wab就是B點的電荷的分佈。

然後用Fermi-Dirac分佈函式做啟用函式

但是把β=1 ，εF=0

β≡1/（kB*T）

KB是玻爾茲曼常數

T是溫度

εF系統中電子的化學勢

ε是能量，假設能量是與B點電荷的分佈有關，並且考慮電性讓B點的能量

ε=（-1）*A*Wab

這樣就把Fermi-Dirac分佈函式變成了sigmoid分佈函式

按照Fermi-Dirac的物理意義，S（x）=1/（1+e^(-A*Wab)）的意義就是B粒子佔據能量-A*Wab的機率。比如S（x）=0.1的意思就是在B位置能量為-A*Wab的粒子數可能為0.1個

同理C點就是C粒子佔據能量 -（B*Wbc+D*Wdc）的機率。