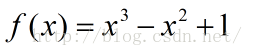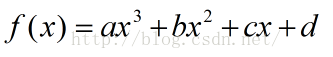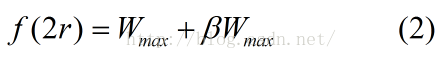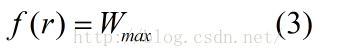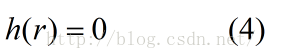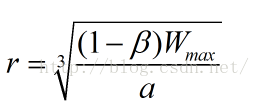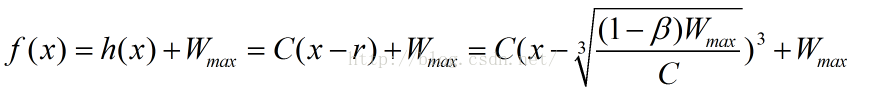TCP擁塞控制算法-從BIC到CUBIC
阿新 • • 發佈:2019-02-16
但我 一點 設置 clas alt 帶寬 upd oss 意義 本文旨在幫助大家理解TCP CUBIC擁塞控制算法背後的點點滴滴以及其方程式為什麽就是那樣子的。一直以來,很多人都覺得CUBIC算法非常復雜,涉及到復雜的天書般的”3次曲線“...然而,CUBIC並不像大家以為的那樣復雜,之所以覺得復雜是因為沒有理解其歷史和背景。
BIC算法
BIC算法對窗口可能的最大值進行二分查找,它基於以下的事實:
1.如果發生丟包的時候,窗口的大小是W1,那麽要保持線路滿載卻不丟包,實際的窗口最大值應該在W1以下;
2.如果檢測到發生丟包,並且已經將窗口乘性減到了W2,那麽實際的窗口值應該在W2以上。
因此,在TCP快速恢復階段過去之後,便開始在W2~W1這個區間內進行二分搜索,尋找窗口的實際最大值。於是定義W1為Wmax,定義W2為Wmin。
以上說的是”道“,接下來我們看一下”術“,即如何驅動整個二分搜索的過程,非常簡單!采用ACK驅動:
每收到一個ACK的時候,便將窗口設置到Wmax和Wmin的中點,一直持續到接近Wmax。
可見BIC的行為是ACK驅動的,而ACK在什麽時候到來是與RTT相關的。這裏,我們先留下一個問題。
在了解了”道“和”術“之後,我們來看一下”勢“。道只是一個原則,對待所有人都是一樣,而術則是實現這個原則的途徑,每個人都有不同,然而最終決定誰能獨霸天下的是勢,這就是說,在領會了道,並且得到了術之後,接下來就要進入爭奪階段了。BIC算法已經在沒有丟包的情況下無限接近了Wmax,這意味著帶寬有空閑資源了,此次的最大帶寬已經不止Wmax了,而是大於Wmax的一個值!問題是,如何找到它!在說如何找到它的方法之前,先說一下怎麽知道已經找到了它,答案就是丟包。
超越Wmax之後,如何找到新的Wmax呢?
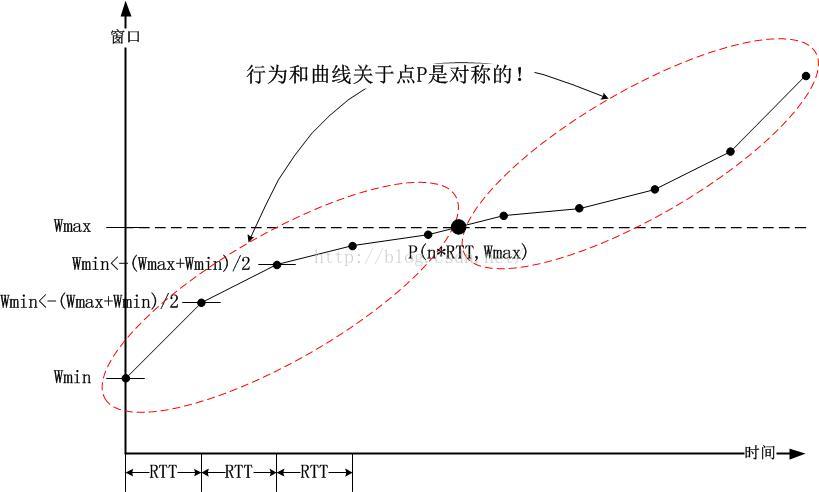
也非常簡單!既然度過了Wmax都沒有丟包,說明新的Wmax還沒有達到,此時BIC采取了一種非常簡單直接的方法:按照逼近Wmax的路徑倒回去,即采用與之對稱的方案。
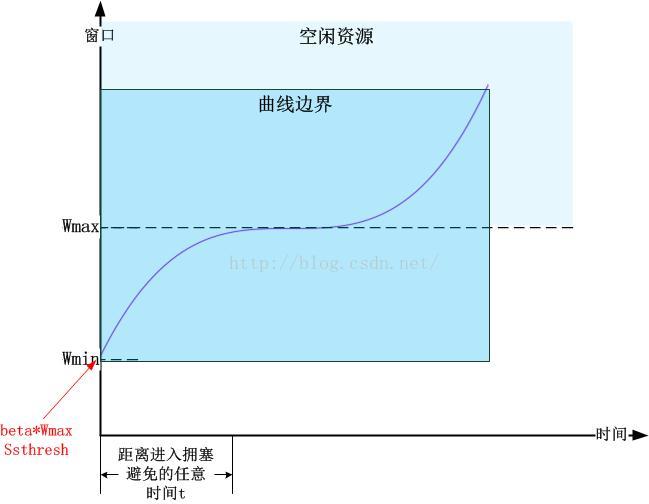
以上整個的道,法,勢三者總結成了以下的圖示:
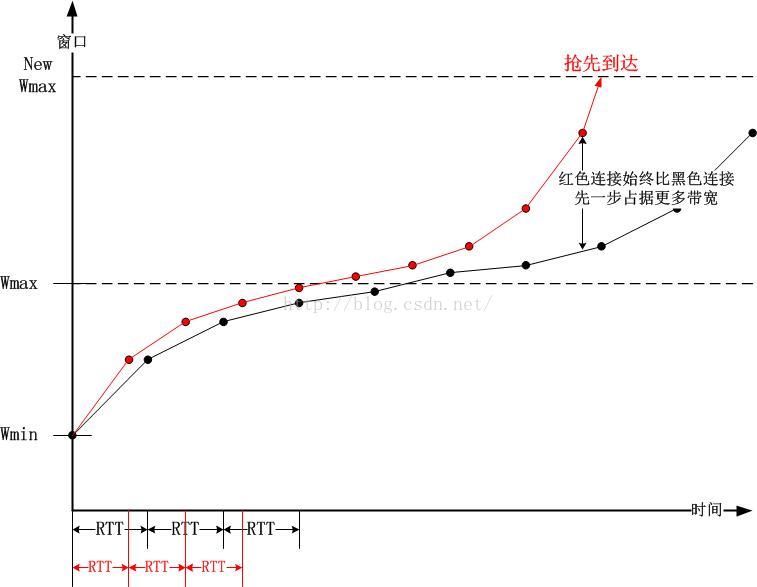
兩個RTT不同的連接,其通過BIC算法搜索到Wmax的時間是不同,進而其進入Max-Probe階段也是不同的,因此空閑的帶寬會被RTT短的那個連接無情的占有:
當然,BIC算法遠不止上面說的那麽簡單,以上的圖解僅僅是理論上的,涉及到實現的時候就不得不考慮TCP運行時的行為特征,比如下圖所示的問題:
----------------------------------------------------------------
我們已經看到了BIC的半景全貌,知道了它存在的兩個問題:
公平性的問題
TCP對帶寬的利用並不是親王掃六合的過程,更像是近代歐洲均勢。所以說,搶帶寬的算法都是傻逼算法。
感官上不那麽美觀的問題
數學上追求的是既然原理上是一個公式,在實現上也必須是一個公式,不能加入更多的現實約束。
----------------------------------------------------------------
解決這些問題的過程導致了CUBIC的誕生!
值得註意的是,BIC和CUBIC在命名上特別有意思,BIC是Binary Increase Congestion的首字母縮寫,而CUBIC並不是BIC加上了"CU-"前綴(-CU前綴是什麽??)...CUBIC不是什麽縮寫,它本來就是”立方“的形容詞全稱,而立方在數學上也是”3次方“的意思,因此顧名思義,CUBIC采用了數學函數即cubic curve的方式,而不是通過ACK到達後的處理行為(B)inary (I)ncrease (C)ongestion來探測窗口。在命名上,這是值得註意的。
註解:後面由於會涉及到簡單的數學公式,由於在文字中插入希臘字母很不方便,因此凡是數學公式中的希臘字母,我在正文中一律寫成其英文音譯,比如我會用beta來表示希臘字母裏相應讀音的那個很像大寫B的字母。
要做到一個在時間上公平的窗口探測行為,就要讓所有的連接的類似BIC那樣的探測曲線是一致的,也就是說所有TCP連接的探測曲線相同!怎麽做到的呢?很簡單。找一條數學上定義的曲線即可!該曲線的曲線方程自變量裏沒有RTT就好了。
我們知道,在二維笛卡爾坐標系中,曲線的自變量只有一個,我們定義其為絕對時間即可,而這只與從曲線開始畫到收到ACK的絕對時間差有關,絕對時間無論對待誰都是公平的!現在的問題是,如何定義曲線本身,讓其看上去比較像BIC的探測曲線。首先一個問題,它應該是幾次曲線呢(我們當然已經知道了它是3次曲線,但這裏給的是一個過程而不是結論!)?
我們註意觀察BIC的曲線,我們發現這是一條其增長率開始很大,慢慢變小,趨近於0,然後再慢慢變大的過程...
考慮到了變化率,不由就想到了導數。現在的問題轉化為了:
誰的導數是慢慢變小,變成0後再慢慢變大的呢?
在找到最終的曲線之前,我們先要找到導數本身的曲線,然後升階即可。問題越來越顯得容易了。學過高中數學的人基本都知道二次曲線滿足這個導數曲線的要求,我們以下面這個二次曲線為例:
確定了曲線的形狀之後,最終我們要確定曲線的參數,最終曲線的方程應該是:
確定待定系數的第一步,也是最重要的一步,就是確定曲線方程的形式。這一步很重要!它甚至比對曲線的形狀的認知更加重要。如果沒有對方程形式的確定,僅僅依靠曲線上的兩個點來待定3次曲線方程的系數,就像解不定方程一樣,變成一種技巧活了。反之,一旦確定了曲線方程的形式,那麽求待定系數的過程就非常簡單了!
我們知道,曲線是對稱的,由凸凹兩部分組成(這到底是CUBIC曲線擬合BIC曲線,還是要反過來呢? :-(),由於CUBIC曲線事實上是一個有界的對稱曲線,在最終參數確定的時候,曲線在橫軸的中點r也是確定的,我們觀察最終的曲線,發現橫軸中點位置正好在縱軸到達Wmax,再看曲線的左界,當曲線在初始的時刻,W從快速恢復的結束位置開始增長,即ssthresh這個值的位置:
我們要做的是使用待定系數法來構造方程,然後求出這些系數並給出其物理意義。
但我們不是真的要按照f(x)的二項式表示去求其系數a,b,c,d,而是將其構造成更加合理的形式。
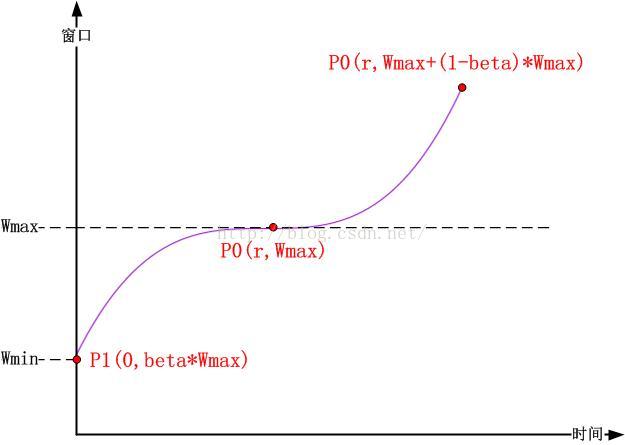
註意到曲線上有三個點是特殊的,如下圖所示:
註意到另外兩個點對曲線的約束,從曲線關於點P(r,Wmax)對稱,我們可以得知:
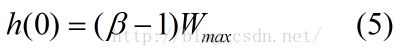
由(4),(5),我們可以構造出h(x)的一個合理形式:
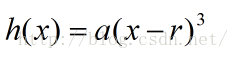
根據上述的(4)和(5),我們得到r的表達式:
到這裏,你可能覺得這越來越復雜了,但事實上,這推導非常簡單,而且,推導結束了,這就是CUBIC的最後結果!我們把上式中的系數a換成C(CUBIC的Paper上寫的就是C,另外,r也要換成K...),那麽最終的式子就是:
對於一次從快速恢復結束的時刻到丟包的擁塞避免過程,我們假設發生丟包時的窗口大小為Wmax,並且假設網絡中沒有別的連接,那麽窗口探測曲線在每一輪擁塞探測過程都是相同的,因此,我們認為Wmax是常數。非常顯然,beta決定了整個曲線對稱範圍圍成區域的高度,而r則控制了從起始窗口到達丟包窗口的時間,由於r與C成反比,那麽C越大,則探測到最大窗口的時間越短,反之則越久。由此,我們只要控制beta和C兩個參數,就能控制CUBIC算法的行為了。
現在知道CUBIC曲線的細節了嗎?好吧,我們一直在數學公式裏徘徊,現在終於要回到TCP了!我們看一下曲線中的beta和a(也就是C)分別影響了TCP的什麽特性,正如CUBIC的Paper上所述:
beta控制了TCP Friendliness
C控制了TCP的收斂速度
在我分析了bbr算法之後,我曾經說過,bbr算法非常簡單,到此為止,你是不是也覺得CUBIC也是很簡單呢?在你給出肯定回答之前,我必須澄清它們的一點區別。
bbr算法就是其行為本身的描述,而CUBIC算法則是借用了一條數學上很優美的曲線方程,這條3次曲線並不關聯任何TCP的行為,換句話說,如果有更好的選擇,也可以不使用這條曲線。這一點與ECC算法(橢圓曲線加密算法)的背景十分不一樣,ECC算法脫離不了橢圓曲線,正是在該曲線上的群,環,域的計算定義了整個算法過程。區別這兩點,對於優化CUBIC是十分重要的。
如果我明明知道在探測到Wmax的時候已經近乎擁塞,那CUBIC曲線還傻傻的去猛往上探測直到丟包,這樣還合適嗎?顯然是不合適的。因此我們可能需要一條不對稱的CUBIC曲線!比如在穩定階段陡一點,在探測階段緩一點,這可能最終會進化到bbr算法類似的效果!
但是,我真的需要另外一條曲線嗎??完美主義者或者數學潔癖者可能特別希望用一個方程式描述這種不對稱的曲線,但如果僅僅想在工程上實現這個理念,完全沒有必要去尋找什麽曲線,直接使用不對稱的曲線即可。
我不再深入闡述這個話題,我只展示一下Linux CUBIC的代碼之修改。對bictcp_update進行修改:
CUBIC曲線由參數確定。
BIC曲線由行為確定。
BIC/CUBIC的收斂靠事件觸發,bbr收斂靠自身伺服機制觸發。
本文就是介紹CUBIC的歷史和背景的...
BIC算法
BIC算法對窗口可能的最大值進行二分查找,它基於以下的事實:1.如果發生丟包的時候,窗口的大小是W1,那麽要保持線路滿載卻不丟包,實際的窗口最大值應該在W1以下;
2.如果檢測到發生丟包,並且已經將窗口乘性減到了W2,那麽實際的窗口值應該在W2以上。
因此,在TCP快速恢復階段過去之後,便開始在W2~W1這個區間內進行二分搜索,尋找窗口的實際最大值。於是定義W1為Wmax,定義W2為Wmin。
以上說的是”道“,接下來我們看一下”術“,即如何驅動整個二分搜索的過程,非常簡單!采用ACK驅動:
每收到一個ACK的時候,便將窗口設置到Wmax和Wmin的中點,一直持續到接近Wmax。
可見BIC的行為是ACK驅動的,而ACK在什麽時候到來是與RTT相關的。這裏,我們先留下一個問題。
在了解了”道“和”術“之後,我們來看一下”勢“。道只是一個原則,對待所有人都是一樣,而術則是實現這個原則的途徑,每個人都有不同,然而最終決定誰能獨霸天下的是勢,這就是說,在領會了道,並且得到了術之後,接下來就要進入爭奪階段了。BIC算法已經在沒有丟包的情況下無限接近了Wmax,這意味著帶寬有空閑資源了,此次的最大帶寬已經不止Wmax了,而是大於Wmax的一個值!問題是,如何找到它!在說如何找到它的方法之前,先說一下怎麽知道已經找到了它,答案就是丟包。
超越Wmax之後,如何找到新的Wmax呢?
也非常簡單!既然度過了Wmax都沒有丟包,說明新的Wmax還沒有達到,此時BIC采取了一種非常簡單直接的方法:按照逼近Wmax的路徑倒回去,即采用與之對稱的方案。
以上整個的道,法,勢三者總結成了以下的圖示:
兩個RTT不同的連接,其通過BIC算法搜索到Wmax的時間是不同,進而其進入Max-Probe階段也是不同的,因此空閑的帶寬會被RTT短的那個連接無情的占有:
當然,BIC算法遠不止上面說的那麽簡單,以上的圖解僅僅是理論上的,涉及到實現的時候就不得不考慮TCP運行時的行為特征,比如下圖所示的問題:
這帶來了BIC實現上的醜陋和復雜性,會有很多的if-else出現,這在感官上很不舒服。
----------------------------------------------------------------
我們已經看到了BIC的半景全貌,知道了它存在的兩個問題:
公平性的問題
TCP對帶寬的利用並不是親王掃六合的過程,更像是近代歐洲均勢。所以說,搶帶寬的算法都是傻逼算法。
感官上不那麽美觀的問題
數學上追求的是既然原理上是一個公式,在實現上也必須是一個公式,不能加入更多的現實約束。
----------------------------------------------------------------
解決這些問題的過程導致了CUBIC的誕生!
值得註意的是,BIC和CUBIC在命名上特別有意思,BIC是Binary Increase Congestion的首字母縮寫,而CUBIC並不是BIC加上了"CU-"前綴(-CU前綴是什麽??)...CUBIC不是什麽縮寫,它本來就是”立方“的形容詞全稱,而立方在數學上也是”3次方“的意思,因此顧名思義,CUBIC采用了數學函數即cubic curve的方式,而不是通過ACK到達後的處理行為(B)inary (I)ncrease (C)ongestion來探測窗口。在命名上,這是值得註意的。
註解:後面由於會涉及到簡單的數學公式,由於在文字中插入希臘字母很不方便,因此凡是數學公式中的希臘字母,我在正文中一律寫成其英文音譯,比如我會用beta來表示希臘字母裏相應讀音的那個很像大寫B的字母。
CUBIC算法
我們先看下CUBIC是怎麽做到窗口探測過程與RTT無關的。要做到一個在時間上公平的窗口探測行為,就要讓所有的連接的類似BIC那樣的探測曲線是一致的,也就是說所有TCP連接的探測曲線相同!怎麽做到的呢?很簡單。找一條數學上定義的曲線即可!該曲線的曲線方程自變量裏沒有RTT就好了。
我們知道,在二維笛卡爾坐標系中,曲線的自變量只有一個,我們定義其為絕對時間即可,而這只與從曲線開始畫到收到ACK的絕對時間差有關,絕對時間無論對待誰都是公平的!現在的問題是,如何定義曲線本身,讓其看上去比較像BIC的探測曲線。首先一個問題,它應該是幾次曲線呢(我們當然已經知道了它是3次曲線,但這裏給的是一個過程而不是結論!)?
我們註意觀察BIC的曲線,我們發現這是一條其增長率開始很大,慢慢變小,趨近於0,然後再慢慢變大的過程...
考慮到了變化率,不由就想到了導數。現在的問題轉化為了:
誰的導數是慢慢變小,變成0後再慢慢變大的呢?
在找到最終的曲線之前,我們先要找到導數本身的曲線,然後升階即可。問題越來越顯得容易了。學過高中數學的人基本都知道二次曲線滿足這個導數曲線的要求,我們以下面這個二次曲線為例:
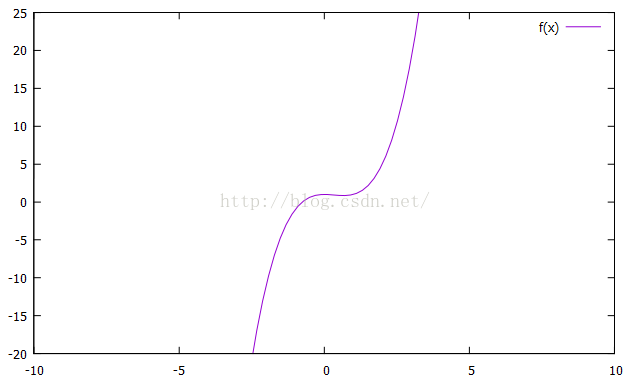
然後畫出其圖形後發現它可以完美詮釋BIC窗口探測曲線的斜率走勢:
這條導數曲線對應的原始曲線就是一條3次曲線:
以上這個僅僅是個例子,我們的目的在於確定CUBIC的曲線形狀,是的,最終的CUBIC曲線就是這樣子的,是不是跟BIC的窗口探測曲線很像呢?
確定了曲線的形狀之後,最終我們要確定曲線的參數,最終曲線的方程應該是:
完成確定待定系數這一步,我們就可以徹底理解CUBIC那看似復雜的方程式背後的所有了。
確定待定系數的第一步,也是最重要的一步,就是確定曲線方程的形式。這一步很重要!它甚至比對曲線的形狀的認知更加重要。如果沒有對方程形式的確定,僅僅依靠曲線上的兩個點來待定3次曲線方程的系數,就像解不定方程一樣,變成一種技巧活了。反之,一旦確定了曲線方程的形式,那麽求待定系數的過程就非常簡單了!
我們知道,曲線是對稱的,由凸凹兩部分組成(這到底是CUBIC曲線擬合BIC曲線,還是要反過來呢? :-(),由於CUBIC曲線事實上是一個有界的對稱曲線,在最終參數確定的時候,曲線在橫軸的中點r也是確定的,我們觀察最終的曲線,發現橫軸中點位置正好在縱軸到達Wmax,再看曲線的左界,當曲線在初始的時刻,W從快速恢復的結束位置開始增長,即ssthresh這個值的位置:
這個位置,就是beta*Wmax!
我們要做的是使用待定系數法來構造方程,然後求出這些系數並給出其物理意義。
但我們不是真的要按照f(x)的二項式表示去求其系數a,b,c,d,而是將其構造成更加合理的形式。
註意到曲線上有三個點是特殊的,如下圖所示:
並且註意到曲線本身是關於P(x=r,y=Wmax)這個點對稱的,我們確定曲線方程的常數因子就是Wmax。因此,我們可以簡單的將曲線方程寫成以下的形式:
現在的目標就是求h(x)。
註意到另外兩個點對曲線的約束,從曲線關於點P(r,Wmax)對稱,我們可以得知:
以及
其中
由以上三式(1),(2),(3)以及(0)得知:
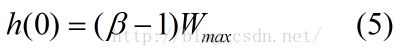
由(4),(5),我們可以構造出h(x)的一個合理形式:
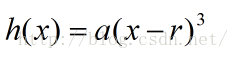
根據上述的(4)和(5),我們得到r的表達式:
##不得不承認以上是一個很合理的解
到這裏,你可能覺得這越來越復雜了,但事實上,這推導非常簡單,而且,推導結束了,這就是CUBIC的最後結果!我們把上式中的系數a換成C(CUBIC的Paper上寫的就是C,另外,r也要換成K...),那麽最終的式子就是:
OK!結束了。現在我們來看下這個式子裏面的兩個參數beta和C,分別代表什麽,或者更加形象的,它們分別控制著什麽。
對於一次從快速恢復結束的時刻到丟包的擁塞避免過程,我們假設發生丟包時的窗口大小為Wmax,並且假設網絡中沒有別的連接,那麽窗口探測曲線在每一輪擁塞探測過程都是相同的,因此,我們認為Wmax是常數。非常顯然,beta決定了整個曲線對稱範圍圍成區域的高度,而r則控制了從起始窗口到達丟包窗口的時間,由於r與C成反比,那麽C越大,則探測到最大窗口的時間越短,反之則越久。由此,我們只要控制beta和C兩個參數,就能控制CUBIC算法的行為了。
現在知道CUBIC曲線的細節了嗎?好吧,我們一直在數學公式裏徘徊,現在終於要回到TCP了!我們看一下曲線中的beta和a(也就是C)分別影響了TCP的什麽特性,正如CUBIC的Paper上所述:
beta控制了TCP Friendliness
C控制了TCP的收斂速度
【註意,上面式子裏的r就是K,CUBIC的Paper上說,K決定了從beta*Wmax到Wmax的時間:K is the time period that the above function takes to increase W to Wmax when there is no further loss event
】
由於CUBIC曲線在穩定擁塞避免階段(Steady State)和空閑資源探測階段(Max Probing)是對稱的,因此我們把收斂速度理解成兩個方面,一方面,它決定了在穩定的擁塞避免階段TCP的擁塞窗口到達最大窗口的時間,另一方面,它在空閑資源的探測階段又決定了探測到新的最大窗口所需的時間。這種對稱的行為,它真的合理嗎??
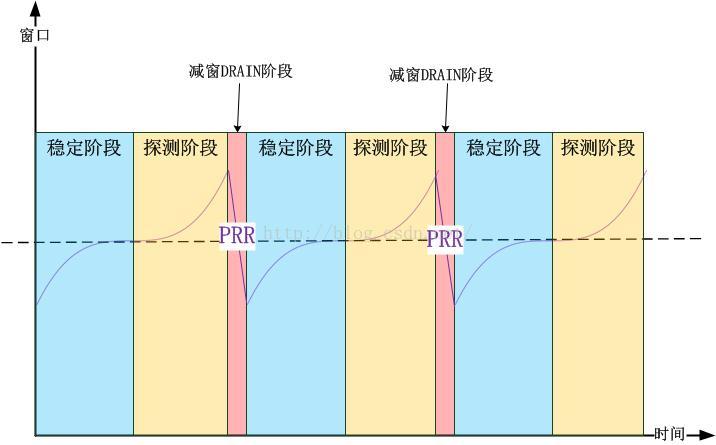
最後,我將CUBIC的算法運行和通用的TCP擁塞控制算法進行映射,我發現它毫不特殊,運行CUBIC算法的TCP連接,也分別會將運行階段映射為三個階段中的一個,分別為穩定階段(Steady State),即不丟包的階段,新空閑資源探測階段,即探測新最大窗口的階段(Max Probing),以及公平收斂階段,即減少數據發送量的階段(類似PRR降窗過程),和bbr不同的是,CUBIC的公平收斂階段不是自己算法控制的(PRR),而bbr則是自己控制的(默認運行1個周期,其後持續運行6個恒穩周期,bbr的周期是一個伺服循環:1個Max Probing-1個Drain-6個Steady State-...)。CUBIC的總體運行如下圖所示:
後記
到此,我覺得本文該要結束了。我個人認為,本文最大的成就感在於,比較明了地解釋了CUBIC這個3次曲線的內部到底是什麽樣子的以及為什麽是這個樣子。很多人搞不清楚它的真面目,覺得它怎麽可以這麽復雜,事實上,CUBIC一點都不復雜!它是由BIC算法一步步衍生出來的。如果按照正常的推導,那些參數都是可以自己確定的,毫無任何神秘之處。那麽BIC算法呢?更加簡單,收到ACK包後執行二分查找驅動的一個過程而已。在我分析了bbr算法之後,我曾經說過,bbr算法非常簡單,到此為止,你是不是也覺得CUBIC也是很簡單呢?在你給出肯定回答之前,我必須澄清它們的一點區別。
bbr算法就是其行為本身的描述,而CUBIC算法則是借用了一條數學上很優美的曲線方程,這條3次曲線並不關聯任何TCP的行為,換句話說,如果有更好的選擇,也可以不使用這條曲線。這一點與ECC算法(橢圓曲線加密算法)的背景十分不一樣,ECC算法脫離不了橢圓曲線,正是在該曲線上的群,環,域的計算定義了整個算法過程。區別這兩點,對於優化CUBIC是十分重要的。
附1:優化和靈活性
既然TCP擁塞算法是借用了一條3次曲線,那麽這條曲線就不是必須的!仔細觀察本文最後的那幅圖,和BIC算法一樣,CUBIC算法在穩定階段和探測階段是對稱的,但是非得這樣嗎?如果我明明知道在探測到Wmax的時候已經近乎擁塞,那CUBIC曲線還傻傻的去猛往上探測直到丟包,這樣還合適嗎?顯然是不合適的。因此我們可能需要一條不對稱的CUBIC曲線!比如在穩定階段陡一點,在探測階段緩一點,這可能最終會進化到bbr算法類似的效果!
但是,我真的需要另外一條曲線嗎??完美主義者或者數學潔癖者可能特別希望用一個方程式描述這種不對稱的曲線,但如果僅僅想在工程上實現這個理念,完全沒有必要去尋找什麽曲線,直接使用不對稱的曲線即可。
我不再深入闡述這個話題,我只展示一下Linux CUBIC的代碼之修改。對bictcp_update進行修改:
curr_C = cube_rtt_scale;
// base_mdev的含義是,剛進入擁塞避免穩定狀態時的mdev,而curr_mdev則是當前的mdev
if (ca->base_mdev && ca->curr_mdev && t > ca->dragon_K) {
if (ca->curr_mdev > ca->base_mdev) // 如果RTT變得比較更加抖動,說明丟包可能性比較大
curr_C >>= 1; // 僅為一例,旨在伸展曲線寬度
if (ca->base_mdev < ca->curr_mdev)
curr_C <<= 1; // 旨在壓縮曲線寬度
}
delta = (cube_rtt_scale * offs * offs * offs) >> (10+3*BICTCP_HZ);
...附2:總結和記錄
為什麽在丟包的時候窗口要減到一個很低的值,而不是僅僅減去1或者2呢?請研究我之前貼的那個TCP公平性收斂圖。CUBIC曲線由參數確定。
BIC曲線由行為確定。
BIC/CUBIC的收斂靠事件觸發,bbr收斂靠自身伺服機制觸發。
再分享一下我老師大神的人工智能教程吧。零基礎!通俗易懂!風趣幽默!還帶黃段子!希望你也加入到我們人工智能的隊伍中來!https://blog.csdn.net/jiangjunshow
TCP擁塞控制算法-從BIC到CUBIC