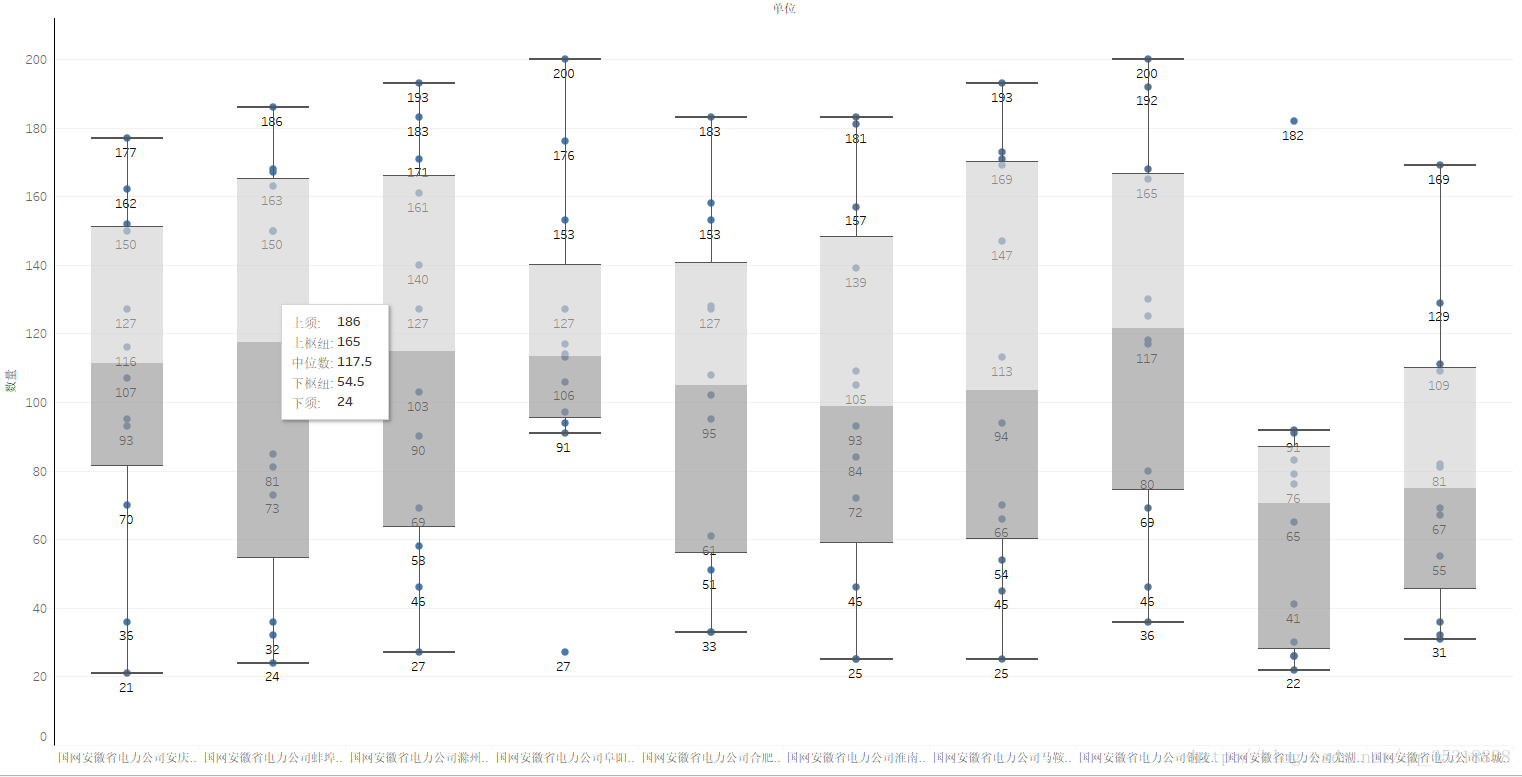
盒須圖
背景：專案的應用場景建設，使用到了tableau的盒須圖，卻對這個盒須圖的幾個引數不理解
涉及的概念：四分位數，插值法

一、四分位數

定義：在統計學中，將一組資料由小到大排序分為四份，其中的三個分割點就是四分位數
英文：Quartile（介紹英文的原因是四分位數的命名就是以英文的第一個字母開頭的）
概念：

• 第一四分位數（Q1）：一組資料由小到大排序，處於所有資料1/4位置的數字；
• 第二四分位數（Q2）：一組資料由小到大排序，處於所有資料1/2位置的數字；
• 第三四分位數（Q3）：一組數由小到大排序呢，處於所有資料3/4為主的數字；
• 四分位距：第一四分位數與第三四分位數的距離

計算方式：

n+1方式：Ｑ１＝（ｎ＋１）×０．２５
ｎ－１方式：Ｑ１＝１＋（ｎ－１）×０．２５

這裡演示的是ｎ－１的方式

資料：1,2,3,4,5,6
Ｑ１的位置：１＋（６－１）×０．２５＝２．２５
Ｑ２的位置：１＋（６－１）×０．５＝３．２５
Ｑ３的位置：１＋（６－１）×０．７５＝４

這裡的位置資料有兩個小數，所有需要用到插值法。
Q1的位置為2.25，也就是第二個數與第三個數之間，那麼利用插值法計算

Q1=2*（1-0.25）+3*（1-0.75）=2.25

注意：這裡的2.25與上面的2.25有本質的區別，加入這一組數為1,2,5,6,7,8
因為陣列的個數沒變，還是6個，所以四分位數的位置沒有變，依舊是上面的三個數，但是資料卻變了，還是使用插值法

Q1=2*（1-0.25）+5（1-0.75）=3.75

插值法的教科書版本很麻煩，這裡的可以簡單理解為較小的數乘以（1-位置中的小數）加上較大的數乘以（位置中的小數）

二、盒須圖

盒須圖見上圖
六個引數

• 上須：最大值
• 下須：最小值
• 上樞紐：Q3
• 下樞紐：Q2
• 中位數：Q1
• 異常值：離散於整個陣列，上面的盒須圖中從左到右的第四個和第九個就有兩個異常值

盒須圖的意義：通過盒須圖可以一眼看出一組數的離散程度，聚集區間（在整個陣列中的四等分中那個區間資料比較集中）