DX雜記之細分著色器和利用貝塞爾曲面平滑模型

阿新 • • 發佈：2019-02-17

細分著色器的構成

細分著色器是為了將一大塊的區域繼續劃分，劃分成很多的小塊
大體上由三部分構成，但也會涉及一些其它階段的內容。
這三個階段分別為 Hull Shader Stage, Tesslator Stage, Domain Shader Stage，他們需要一起工作，從名字就可以看出來是兩個可程式設計著色器階段中間夾著一個可配置階段，具體順序如圖

第一部分：Hull Shader

首先先來看一段 Hull Shader 的程式碼

//--------------------------------------------------------------------------------
struct HS_CONTROL_POINT_INPUT
{
	float3 WorldPosition	: POSITION;
};
//--------------------------------------------------------------------------------
struct HS_CONTROL_POINT_OUTPUT
{
	float3 WorldPosition	: POSITION;
};
//--------------------------------------------------------------------------------
struct HS_CONSTANT_DATA_OUTPUT
{
    float Edges[3]			: SV_TessFactor;
	float Inside			: SV_InsideTessFactor;
};
//--------------------------------------------------------------------------------

//--------------------------------------------------------------------------------
HS_CONSTANT_DATA_OUTPUT PassThroughConstantHS( 
	InputPatch<HS_CONTROL_POINT_INPUT, 3> ip, 
    uint PatchID : SV_PrimitiveID )
{	
    HS_CONSTANT_DATA_OUTPUT output;

	output.Edges[0] = 2.0f;
	output.Edges[1] = 2.0f;
	output.Edges[2] = 2.0f;

	output.Inside = 2.0f;

    return output;
}
//--------------------------------------------------------------------------------
[domain("tri")]
[partitioning("fractional_even")]
[outputtopology("triangle_cw")]
[outputcontrolpoints(3)]
[patchconstantfunc("PassThroughConstantHS")]

HS_CONTROL_POINT_OUTPUT HSMAIN( 
    InputPatch<HS_CONTROL_POINT_INPUT, 3> ip, 
    uint i : SV_OutputControlPointID,
    uint PatchID : SV_PrimitiveID )
{
    HS_CONTROL_POINT_OUTPUT output;

    output.WorldPosition = ip[i].WorldPosition;

    return output;
}
//--------------------------------------------------------------------------------

從這個程式碼片段來看，實現由兩部分組成

一部分是 shader program 本體，主要是用來傳遞 control point (與頂點基本類似，但有小小的差別) 和其他引數
另一部分是在 [patchconstantfunction] 屬性中定義的，用於得到細分常量引數的方法，後面的階段會根據這裡提供的引數進行細分，程式碼中是 PassThroughConstantHS 方法

這裡面有幾點要知道的知識點

方法的呼叫順序：shader program 先於 constant function 執行
control points 與 vertex 的內容沒有什麼差別，唯一區別在於如果管線配置要使用細分著色器的話，必須定義control point patch list中的其中一種圖形型別，即設定D3D11_PRIMITIVE_TOPOLOGY的值。(typedef D3D_PRIMITIVE_TOPOLOGY D3D11_PRIMITIVE_TOPOLOGY;)。所以 control points 除了頂點有的資訊之外，它們是被包括在 patch 中的比頂點多了這份連線資訊的頂點

Input and Output Patches：他們都是用來獲取一組 control points 的資料的。Input Patch 作為 hull shader, patch constant function, 和 geometry shader 的輸入。Output Patch 作為 domain shader 的輸入。
shader program 的 [attribute]
- [domain(tri)]：確定輸出至 domain shader 的 patch 型別，常用 "tri" 和 "quad"
- [partitioning("fractional_odd")]：影響下一個配置階段對引數進行插值處理的方式，共有四種類型：integer，fractional_even，fraction_odd，pow2
- [outputtopology(triangle_cw)]：用於指導 tessellator 重新將單獨的點組裝成圖元，可選項還有 triangle_ccw 和 line
- [outputcontrolpoints(3)]：輸出的 control point 數量
- [patchconstantfunc("PassThroughConstantHS")]：上文說過，宣告方法
- [maxtessfactor(5)]：定義 patch constant function 產生的最大的 tessellation facto

然後我們開始分析一下當前方法做了些什麼：

拆分原有傳遞進來的 patch，根據它的資訊生成用於構成新的 patch 的 points 和產生一些細分引數
main program：主要是根據 patch 中的 control points 的資訊產生[outputcontrolpoints(n)] 中宣告的數量的輸出資料，作為 OutputPatch 中的 control point 傳遞到 domain shader
- 輸入：
  - SV_OutputControlPointID：uint i : SV_OutputControlPointID 這個是當前呼叫的次數，也就相當於一個 for 迴圈的計數器
  - SV_PrimitiveID：唯一 id
  - InputPatch 上面提過了
- 輸出：
  - 新產生的 points
constant function：
- 決定細分引數
- 兩種細分引數輸出寫入至SV_InsideTessFactor和SV_TessFactor,這兩個引數會指導細分階段劃分patch
- 輸出：
  - SV_InsideTessFactor 和 SV_TessFactor

第二部分：Tessellator

這是一個需要配置的階段，而非可程式設計階段
根據 hull shader 傳遞進來的點去生成圖元資訊給 domain shader
這個階段同樣由兩部分組成
- 根據 SV_TessFactor 和 SV_InsideTessFactor (constant function 儲存引數的系統型別) 的值產生一些座標點
- 用這些座標點來生成圖元傳遞至 domain shader

第三部分：Domain shader

這是細分的最後一個階段，它接收從前面 tessellator 傳過來的座標點，然後產生最終的輸出頂點，而產生輸出頂點最重要的部分也就是計算頂點的位置。之後我們計算貝塞爾曲面的位置也是在這裡，所以這是整個細分最核心的部分
首先還是來看一段這部分的程式碼，大致的瞭解一下

struct DS_OUTPUT
{
    float4 Position			: SV_Position;
};

[domain("tri")]
DS_OUTPUT DSMAIN( 
        const OutputPatch<HS_CONTROL_POINT_OUTPUT, 3> TrianglePatch,
	float3 BarycentricCoordinates : SV_DomainLocation, 
	HS_CONSTANT_DATA_OUTPUT input )
{
	DS_OUTPUT output;

	// Interpolate world space position with barycentric coordinates
	float3 vWorldPos = 
        BarycentricCoordinates.x * TrianglePatch[0].WorldPosition +     
        BarycentricCoordinates.y * TrianglePatch[1].WorldPosition + 
        BarycentricCoordinates.z * TrianglePatch[2].WorldPosition;
	
	// Transform world position with viewprojection matrix
	output.Position = mul( float4(vWorldPos.xyz, 1.0), ViewProjMatrix );
	
	return output;
}

tesselator 階段每產生一個座標點就會呼叫一次，根據輸入引數 OutputPatch<type，num>，數量範圍是 [1 - 32]
輸入：
- OutputPatch<type, n>：整個 patch 的所有資訊
- SV_DomainLocation：在 domain 中的位置，可以理解成類似於 texture sampler 中的 uv
- type：傳遞進來的 patch 中的control points 的結構
輸出：
- SV_Position 和其他資訊

第四部分：生成曲面和輸出頂點計算

結果是為了讓模型生成更加平滑的曲面，造成模型有稜角的原因無非是頂點少，過多的話會影響渲染效能，所以才會用到細分來產生更加平滑的曲面
（小貼士）要產生曲面，那麼生成的點必定不在原本的平面上
還是先放程式碼，然後解釋

cbuffer Transforms
{
    matrix WorldMatrix;
    matrix ViewProjMatrix;
};

cbuffer RenderingParameters
{
	float3 cameraPosition;
	float3 cameraLookAt;
};

cbuffer TessellationParameters
{
    float4 EdgeFactors;
};

//--------------------------------------------------------------------------------
// Inter-stage structures
//--------------------------------------------------------------------------------
struct VS_INPUT
{
    float3 position 		: POSITION;
	float3 normal 			: NORMAL;
	//float2 tex				: TEXCOORDS0;
};

struct VS_OUTPUT
{
    float3 position 		: POSITION;
	float3 normal 			: NORMAL;
};
//--------------------------------------------------------------------------------
struct HS_OUTPUT
{
    float3 position			: POSITION;
	float3 normal 			: NORMAL;
};
//--------------------------------------------------------------------------------
struct HS_CONSTANT_DATA_OUTPUT
{
    float Edges[3]			: SV_TessFactor;
    float Inside            : SV_InsideTessFactor;
};
//--------------------------------------------------------------------------------
struct DS_OUTPUT
{
    float4 Position			: SV_Position;
    float3 Colour			: COLOUR;
};

float ComputeWeight(InputPatch<VS_OUTPUT, 3> inPatch, int i, int j)
{
	return dot(inPatch[j].position - inPatch[i].position, inPatch[i].normal);
}

float3 ComputeEdgePosition(InputPatch<VS_OUTPUT, 3> inPatch, int i, int j)
{
	return ( 
			(2.0f * inPatch[i].position) + inPatch[j].position 
			- (ComputeWeight(inPatch, i, j) * inPatch[i].normal)
			) / 3.0f;
}

float3 ComputeEdgeNormal(InputPatch<VS_OUTPUT, 3> inPatch, int i, int j)
{
	float t = dot
			  (
				inPatch[j].position - inPatch[i].position
				, inPatch[i].normal + inPatch[j].normal
			   );
	
	float b = dot
			  (
				inPatch[j].position - inPatch[i].position
				, inPatch[j].position - inPatch[i].position
			   );
			   
	float v = 2.0f * (t / b);
	
	return normalize
			(
				inPatch[i].normal + inPatch[j].normal 
				- v * (inPatch[j].position - inPatch[i].position)
			);
}

VS_OUTPUT VSMAIN(in VS_INPUT input)
{
    VS_OUTPUT output;

    output.position = mul(float4(input.position, 1.0f), WorldMatrix).xyz;
	output.normal = normalize(mul(input.normal,(float3x3)WorldMatrix));
    
	return output;
}
//--------------------------------------------------------------------------------
HS_CONSTANT_DATA_OUTPUT PassThroughConstantHS(
    InputPatch<VS_OUTPUT, 3> ip,
    uint PatchID : SV_PrimitiveID)
{
    HS_CONSTANT_DATA_OUTPUT output;

    output.Edges[0] = 64.0f;
    output.Edges[1] = 64.0f;
    output.Edges[2] = 64.0f;

    output.Inside = 64.0f;

    return output;
}
//--------------------------------------------------------------------------------
[domain("tri")]
[partitioning("fractional_even")]
[outputtopology("triangle_cw")]
[outputcontrolpoints(13)]
[patchconstantfunc("PassThroughConstantHS")]

HS_OUTPUT HSMAIN(
    InputPatch<VS_OUTPUT, 3> ip,
    uint i : SV_OutputControlPointID,
    uint PatchID : SV_PrimitiveID)
{
    HS_OUTPUT output;

    // Must provide a default definition just in
    // case we don't match any branch below
	output.position = float3(0.0f, 0.0f, 0.0f);
	output.normal = float3(0.0f, 0.0f, 0.0f);	
	
	switch(i)
	{
		// Three actual vertices:
		
		// b(300)
		case 0:
		// b(030)
		case 1:
		// b(003)
		case 2:
		
			output.position = ip[i].position;
            output.normal = ip[i].normal;
			break;
		
		// Edge between v0 and v1
		
		// b(210)
		case 3:
			output.position = ComputeEdgePosition(ip, 0, 1);
			break;
		// b(120)
		case 4:
			output.position = ComputeEdgePosition(ip, 1, 0);
			break;
		
		// Edge between v1 and v2
		
		// b(021)
		case 5:
			output.position = ComputeEdgePosition(ip, 1, 2);
			break;
		// b(012)
		case 6:	
			output.position = ComputeEdgePosition(ip, 2, 1);
			break;
		
		// Edge between v2 and v0
		
		// b(102)
		case 7:
			output.position = ComputeEdgePosition(ip, 2, 0);
			break;
		// b(201)
		case 8:
			output.position = ComputeEdgePosition(ip, 0, 2);
			break;
		
		// Middle of triangle
		
		// b(111)
		case 9:
			float3 E = 
						(
							ComputeEdgePosition(ip, 0, 1) + ComputeEdgePosition(ip, 1, 0)
							+
							ComputeEdgePosition(ip, 1, 2) + ComputeEdgePosition(ip, 2, 1)
							+
							ComputeEdgePosition(ip, 2, 0) + ComputeEdgePosition(ip, 0, 2)
						) / 6.0f;
			float3 V = (ip[0].position + ip[1].position + ip[2].position) / 3.0f;
			
			output.position = E + ( (E - V) / 2.0f );
			
			break;
			
		// Normals
			
		// n(110) - between v0 and v1
		case 10:
			output.normal = ComputeEdgeNormal(ip, 0, 1);
			break;
		
		// n(011) - between v1 and v2
		case 11:
			output.normal = ComputeEdgeNormal(ip, 1, 2);
			break;
		
		// n(101) - between v2 and v0
		case 12:
			output.normal = ComputeEdgeNormal(ip, 2, 0);
			break;
	}	

    return output;
}
//--------------------------------------------------------------------------------
[domain("tri")]
DS_OUTPUT DSMAIN(const OutputPatch<HS_OUTPUT, 13> TrianglePatch,
    float3 BarycentricCoordinates : SV_DomainLocation,
    HS_CONSTANT_DATA_OUTPUT input)
{
	DS_OUTPUT output;

	float u = BarycentricCoordinates.x;
	float v = BarycentricCoordinates.y;
	float w = BarycentricCoordinates.z;
	
	// Original Vertices
	float3 p300 = TrianglePatch[0].position;
	float3 p030 = TrianglePatch[1].position;
	float3 p003 = TrianglePatch[2].position;
	
	// Edge between v0 and v1
	float3 p210 = TrianglePatch[3].position;
	float3 p120 = TrianglePatch[4].position;
	
	// Edge between v1 and v2
	float3 p021 = TrianglePatch[5].position;
	float3 p012 = TrianglePatch[6].position;
	
	// Edge between v2 and v0
	float3 p102 = TrianglePatch[7].position;
	float3 p201 = TrianglePatch[8].position;
	
	// Middle of triangle
	float3 p111 = TrianglePatch[9].position;
	
	// Calculate this sample point
	float3 p = (p300 * pow(w,3)) + (p030 * pow(u,3)) + (p003 * pow(v,3))
			 + (p210 * 3.0f * pow(w,2) * u) 
			 + (p120 * 3.0f * w * pow(u,2)) 
			 + (p201 * 3.0f * pow(w,2) * v)
			 + (p021 * 3.0f * pow(u,2) * v) 
			 + (p102 * 3.0f * w * pow(v,2)) 
			 + (p012 * 3.0f * u * pow(v,2))
			 + (p111 * 6.0f * w * u * v);
	
	//p = w*TrianglePatch[0].position + u*TrianglePatch[1].position + v*TrianglePatch[2].position;
	
	// Transform world position with viewprojection matrix
	output.Position = mul( float4(p, 1.0), ViewProjMatrix );
	
	// Compute the normal - LINEAR
	float3 vWorldNorm = w*TrianglePatch[0].normal + u*TrianglePatch[1].normal + v*TrianglePatch[2].normal;
	
	// Compute the normal - QUADRATIC
	float3 n200 = TrianglePatch[0].normal;
	float3 n020 = TrianglePatch[1].normal;
	float3 n002 = TrianglePatch[2].normal;
	
	float3 n110 = TrianglePatch[10].normal;
	float3 n011 = TrianglePatch[11].normal;
	float3 n101 = TrianglePatch[12].normal;
	
	vWorldNorm = (pow(w,2) * n200) + (pow(u,2) * n020) + (pow(v,2) * n002)
			   + (w * u * n110) + (u * v * n011) + (w * v * n101);
	
	vWorldNorm = normalize( vWorldNorm );
	
	output.Colour = w*TrianglePatch[0].normal+u*TrianglePatch[1].normal+v*TrianglePatch[2].normal;
	
	return output;
}

[maxvertexcount(3)]
void GSMAIN( triangle DS_OUTPUT input[3], inout TriangleStream<DS_OUTPUT> TriangleOutputStream )
{
    TriangleOutputStream.Append( input[0] );
    TriangleOutputStream.Append( input[1] );
    TriangleOutputStream.Append( input[2] );
    TriangleOutputStream.RestartStrip();
}

float4 PSMAIN(in DS_OUTPUT input) : SV_Target
{
    float4 color = float4(input.Colour, 1.0f);

    return(color);
}

先提一下貝塞爾曲線和曲面。
- 一階貝塞爾曲線(線段)：
  
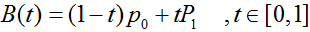
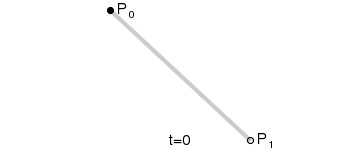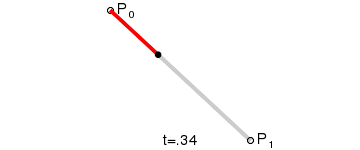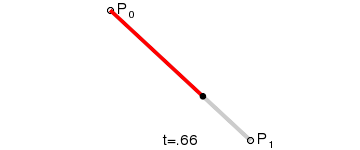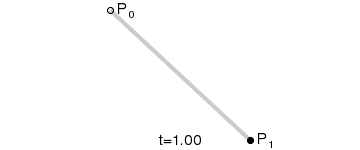
  意義：由 P0 至 P1 的連續點，描述的一條線段
- 二階貝塞爾曲線(拋物線)：
  
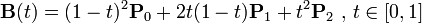
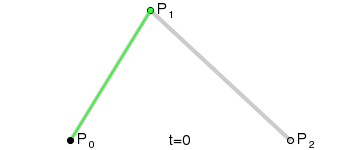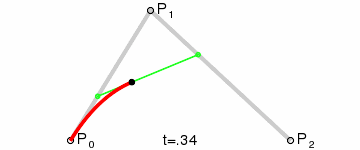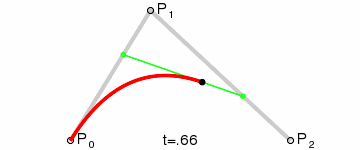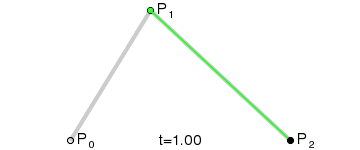
  原理：由 P0 至 P1 的連續點 Q0，描述一條線段。
  由 P1 至 P2 的連續點 Q1，描述一條線段。
  由 Q0 至 Q1 的連續點 B(t)，描述一條二次貝塞爾曲線。
  
  經驗：P1-P0為曲線在P0處的切線。
- 三階貝塞爾曲線：
  
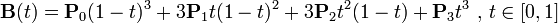
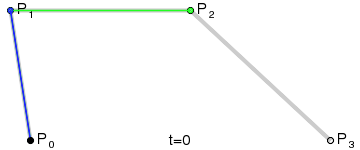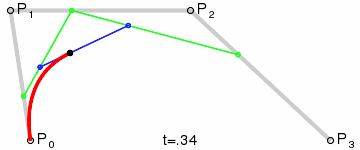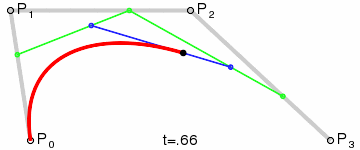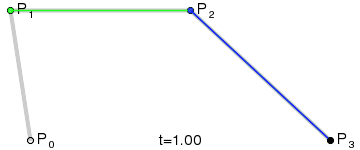
  通用公式：
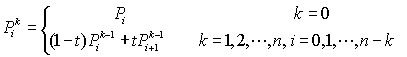
- 貝塞爾曲面：

以上內容出自貝塞爾曲線

說明：看一階就能明白這東西其實就是個插值，不過複雜以後找插值的位置變化了而已
頂點部分：
- 上面的公式看一下大概瞭解了之後，我們要確定的就是 u,v,w 和帶下標的 b 系列，uvw 就是處於 domain 中的位置，也就是上面提到的 SV_DomainLocation，這個就不用關心了。將模型變平滑，也就是將組成模型的三角形變平滑，這些 b 引數就是我們要將一個三角形變平滑需要改變的地方，將一個三角形變成不在同一個平面的10個頂點，如圖：
- 計算十個點：
  - $b_{300} = P_{_{1}}$
  - $b_{030} = P_{_{2}}$
  - $b_{003} = P_{_{3}}$
  - $w_{ij} = (P_{_{j}} - P_{_{i}}) \cdot N_{_{i}}$
  - $b_{210} = (2P_{_{1}} + P_{_{2}} - w_{_{12}}N_{_{1}}) / 3$
  - $b_{120} = (2P_{_{2}} + P_{_{1}} - w_{_{21}}N_{_{2}}) / 3$
  - $b_{021} = (2P_{_{2}} + P_{_{3}} - w_{_{23}}N_{_{2}}) / 3$
  - $b_{012} = (2P_{_{3}} + P_{_{2}} - w_{_{32}}N_{_{3}}) / 3$
  - $b_{102} = (2P_{_{3}} + P_{_{1}} - w_{_{31}}N_{_{3}}) / 3$
  - $b_{201} = (2P_{_{1}} + P_{_{3}} - w_{_{13}}N_{_{1}}) / 3$
  - $E= (b_{_{210}} + b_{_{120}} + b_{_{021}} + b_{_{012}} + b_{_{102}} + b_{_{201}}) / 6$
  - $V = (P_{1} + P_{2} + P_{3}) / 3$
  - $B_{111} = E + (E - V) / 3$
從程式碼中可以看出來，Hull shader 中計算了這十個點然後傳遞至 Domain Shader 中然後通過貝塞爾曲面公式即可得到對應的點，ComputeWeight，ComputeEdgePosition 則是計算公式中的計算過程對應的兩個方法
公式中還有一部分是關於法線的，這是一個比較重要的地方，前面提到了新增加進來的點是不能在一個平面的，得到這個結果的方法就是頂點的法線不能共面，所以這個法線並不是真正的法線，而是 bad normal，如圖頂點 P1 的法線並不是這個平面的法線，如果相同，則計算出來的點依舊共面而不可能達到平滑的效果 ComputeEdgeNormal 即是計算方法
以上是對比圖，可以看到還是平滑了許多的，由於沒有做抗鋸齒，可能邊緣有些鋸齒，先行忽略吧。
然後就到這裡！

DX雜記之細分著色器和利用貝塞爾曲面平滑模型

細分著色器的構成細分著色器是為了將一大塊的區域繼續劃分，劃分成很多的小塊大體上由三部分構成，但也會涉及一些其它階段的內容。這三個階段分別為 Hull Shader Stage, Tesslator Stage, Domain Shader Stage，他們需要一起

unityShader之頂點著色器和片段著色器(一)

頂點著色器和片段著色器作為效能不錯，實現效果也很好的渲染方式，這裡分幾個小結著重說一說，然後所有關鍵字的使用以及特殊語義的含義都在程式碼裡註釋了，有不明白的可以討論下： // Upgrade NOTE: replaced 'mul(UNITY_MATRIX

Android開發之Path的高階用法用貝塞爾曲線繪製波浪線

前言：貝塞爾曲線分為一級曲線，二級曲線，三級曲線和多級曲線，利用貝塞爾曲線可以做出很多有意思的動畫和圖形，今天我們就來實現一個比較簡單的波浪線。 -----------------分割線--------------- 初步認識貝塞爾曲線： mPath.moveTo：設定起點

Unity中利用貝塞爾曲線來實現3D中的曲線運動

下面是在理解後寫的2階三階曲線 using UnityEngine; using System.Collections; using System.Collections.Generic; public class TestCurve : MonoBehaviour

“unity著色器和螢幕特效”學習筆記之rendering mode

unity的rendering mode中有4種渲染模式，主要用來指定物體表面的透明性，下面分別介紹這四種模式的區別，使用貼圖材質帶通道的psd格式的圖片，在Photoshop中的效果如下： 1.Opaque（不透明）：將其運用到unity場景中的物件，如下圖所示，就是

nBodyCS<I>學習筆記之計算著色器

python基礎之叠代器和生成器

see per n) attribute product 原本狀態區別開發假如我現在有一個列表l=[‘a‘,‘b‘,‘c‘,‘d‘,‘e‘]，我想取列表中的內容，有幾種方式？首先，我可以通過索引取值l[0],其次我們是不是還可以用for循環來取值呀？你有沒有仔細

Python之叠代器和生成器

OS 返回內部 16px fun break 得到 urn b- 叠代器一叠代 # 叠代是一個重復的過程，每次重復即一次叠代，並且每次叠代的結果都是下一次叠代的

Python學習之迭代器和生成器

那麼首先什麼是迭代器和生成器呢？迭代器即迭代的工具，那麼什麼又是迭代呢？所謂迭代：迭代是一個重複的過程，每次重讀即一次迭代，並且每次迭代的結果都是下一次迭代的初始值。例： l=[1,2,3] count=0 while count < len(l): print(l[count])

分類器設計之線性分類器和線性SVM(含Matlab程式碼)

對於高維空間的兩類問題，最直接的方法是找到一個最佳的分類超平面，使得並且,對於所有的正負訓練樣本和. 因此，以上問題可以表達為：問題P0可以轉化為兩邊除以\epsilon，並且做變數替換，最終得到下面的線性規化（linear programming

WebGL著色器和Three.js自己定義後期處理著色器

WebGL著色器和Three.js自己定義後期處理著色器為了渲染出一個網格的最終影象，開發者需要準確的定義頂點、變換、材質、光源以及相機是如何相互作用並最終生成影象的。而承擔這個工作的就是著色器（shader）。著色器又稱作可程式設計著色器，它是一段原始碼，它實現了將網格畫素點投影

CSS之分組選擇器和巢狀選擇器

分組選擇器，將一個樣式應用於多個類，或者標籤啥的每個選擇器用逗號隔開 <!DOCTYPE html> <html> <head> <meta charset="utf-8"> <title>菜鳥教程(runoob.c

Python基本語法之迭代器和生成器

迭代器迭代是訪問集合類元素的一種方式，它可以記住遍歷的位置的物件，從集合的第一個元素開始訪問，直到所有的元素被訪問完結束，只能往前不會後退。字串、列表或元組物件都可用於建立迭代器。迭代器有兩個基本的方法：iter()和nex

WebGL學習之從著色器入門

Intro 不論是WebGL、OpenGL、OpenGL ES、Vulkan、DirectX，這些聽起來就十分“底層”、“高效能”、“難寫”的東西似乎是和我一個後端開發都沒什麼關係。（遠處傳來聲音：別tm擅自改臺詞！）咳，迴歸正題。我看了好多的 OpenGL 入門書，固定管線的比較好

Linux之vim編輯器和bash算術運算入門

Linux的命令列介面下面有非常多的文字編輯器。比如經常聽說的就有Emacs、pico、nano、joe與vim等。vim可以看做是vi的高階版。我們為什麼一定要學習vim呢？有以下幾個原因： (1)所有的Unix like系統都會內建vi文字編輯器，其他的文字編輯器則不一定會存在。 (2)

D3D12渲染技術之在著色器中取樣

我們直奔主題，紋理物件在HLSL中定義，並使用以下語法分配給紋理暫存器： Texture2D gDiffuseMap : register(t0); 這個換成在Unity引擎或者UE4引擎中就是提供的視覺化操作介面，而在DX中的表示是按照上面的寫法，這樣可以通過引擎對其進行賦值

人狠話不多，細說大牛直播SDK之RTMP播放器和RTSP播放器

Windows/Android/iOS平臺高穩定、超低延遲的跨平臺RTMP直播播放器； Windows/Android/iOS平臺高穩定、超低延遲的跨平臺RTSP直播播放器； Windows/Android/iOS平臺完美支援多例項播放（如同時播放多路rtmp/rtsp流）； Windows/A

TypeScript基礎入門之迭代器和生成器

迭代性如果物件具有Symbol.iterator屬性的實現，則該物件被視為可迭代。一些內建型別，如Array，Map，Set，String，Int32Array，Uint32Array等，已經實現了Symbol.iterator屬性。物件上的Symbol.iter

OSG使用OpenGL頂點著色器和片元著色器

目的：使用OpenGL著色語言中的頂點和片元著色器，替代原有的固化函式管道的光照和材質計算，用於場景圖形中的節點選擇。（磚塊著色器程式來自3DLabs） ------------------------------------ 概述： OpenGL著色語言允許程式設

C++ 基礎之 "引用形參" 和 "利用const引用避免複製" &

之前兩篇文章裡的兩個函式如下所示： //過載操作符+ Vector3 operator+(const Vector3 &a){ return Vector3(x + a.x,y + a.y,z+a.z); } //比較兩

DX雜記之細分著色器和利用貝塞爾曲面平滑模型

細分著色器的構成

第一部分：Hull Shader

第二部分：Tessellator

第三部分：Domain shader

第四部分：生成曲面和輸出頂點計算

相關推薦